اسپلاین

اسپلاین (spline) در ریاضیات یک تابع هموار چندضابطه‌ای-چندجمله‌ای است.

در مسائل درون‌یابی، معمولاً منظور از درون‌یابی اسپلاین، پیدا کردن چندجمله‌ای درون یابی است، چرا که به همان نتیجه می‌انجامد، حتی در مواقعی که از چندجمله‌ای‌های درجه پایین استفاده می‌شود.
چندجمله‌ای‌های پارا متری از درجات بالا یک ضعف دارند:
برای مثال در شکل زیر پرش ارتفاع در حوالی مرکز داده‌ها باعث تغییر زیادی روی چندجمله‌ای درون یابی شده در نزدیکی انتهای منحنی دارد.

چندجمله‌ای از در جهٔ بالا

در عوض در شکل بعدی از منحنی اسپلاین درجه سوم(cubic spline) در همان نقاط مثال قبل استفاده شده‌است. مشاهده می‌کنید که منحنی چقدر دقیق از نقاط ورودی می‌گذرد. دقت داشته باشید که همواره منحنی‌ها در محل اتصال شکلی یکنواخت دارند.

یک منحنی اسپلاین

منحنی اسپیلاین با استفاده از مشتقات یک منحنی چندجمله‌ای درجه سوم میان هر دو نقطه ورودی ایجاد می‌شود. به عبارتی دیگر، منحنی درجه سوم و تابع چندضابطه‌ای است که از چند تابع چند ضابطه‌ای که به یکدیگر چسبیده‌اند تشکیل شده‌است. این توابع چند ضابطه‌ای آن چنان در محل اتصال با یکدیگر مطابقت دارند که تقریباً محل اتصال مشخص نیست. در حقیقت، اگر تمام تابع با یک تابع ${\displaystyle p(t)}$توصیف شود، ${\displaystyle p(t)}$آن قدر یکنواخت و هموار خواهد بود که دارای مشتق دوم در تمام نقاط و مشتق دوم پیوسته خواهد بود.

اسپلاین درجه سوم(cubic spline)

اسپلاین درجه سوم یک منحنی چند ضابطه‌ای درجه سوم با مشتق دوم پیوسته است.

واژه شناسی اسپلاین

کلمهٔ اسپلاین در حقیقت بازمی‌گردد به نوار باریکی از جنس چوب یا فلز. در گذشته منحنی‌ها برای طراحی کشتی‌ها و هواپیماها با قرار دادن دقیق منحنی‌هایی از نوارهای باریک چوب یا فلز در بدنهٔ آن‌ها به گونه‌ای که ضمن گذشتن از نقاط دلخواه انعطاف‌پذیر نیز باشند. به دلایل فیزیکی، این چنین منحنی‌هایی تقریباً چند ضابطه ای‌هایی درجه سوم با مشتق دوم پیوسته‌اند، در صورتی که به درستی پارامتری شوند.

ممکن است که از ریاضیات بیاد آورید انحنای هر منحنی در هر نقطه به مشتق دوم منحنی در آن نقطه وابسته است. در نقاط انتهایی، یک نوار واقعی از چوب یا فلز خم نمی‌شود، و مشتق دوم این منحنی صفر است.

منحنی اسپلاین درجه سوم ریلکس(relaxed cubic spline)

منحنی اسپلاین درجه سوم را ریلکس می‌نامند، اگر مشتق دوم در هر انتها صفر شود ما می‌بایستی تمرکز خود را روی منحنی‌های اسپلاین درجه سوم ریلکس قرار دهیم. همانگونه که خواهید دید، از این منحنی‌ها می‌توان برای طراحی‌های کنترل شده(b-spline) یا برای درون یابی استفاده کرد. برای تشریح ضابطه‌های از درجهٔ سوم به صورت ساده و قرادادی، می‌بایستی از منحنی‌های بی زی ای(bَezier) استفاده کنیم.

منحنی‌های بی زی ای با مشتق دوم صفر در یک انتها

به منظور ارضای شرط ریلکس بودن انتهای منحنی، می‌بایستی بتوانیم تشخیص دهیم که چه زمانی یک منحنی بی زی ای دارای مشتق دوم صفر در یک انتها می‌باشد. برای یک منحنی بی زی ای درجه سوم با تا بع${\displaystyle P(t)}$ و نقاط کنترلی${\displaystyle {{P}_{0}}-{{P}_{1}}-{{P}_{2}}-{{P}_{3}}}$داریم:

${\displaystyle {P}''(0)=6({{P}_{0}}-2{{P}_{1}}+{{P}_{2}})}$

این معادله زمانی صفر می‌شود که:

${\displaystyle 2{{P}_{1}}={{P}_{0}}+{{P}_{2}}}$

و یا متعاقباً:

شکل ۳

${\displaystyle {{P}_{1}}={\frac {1}{2}}{{P}_{0}}+{\frac {1}{2}}{{P}_{2}}}$

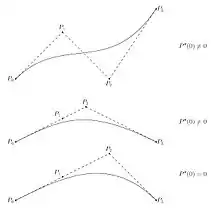
رابطه‌ای مشابه در مورد${\displaystyle {P}''(1)=0}$ برقرار است. حتی ساده‌تر: ${\displaystyle {P}''(0)=0}$ اگر و تنها اگر ${\displaystyle P}$eنقطهٔ میانی المان${\displaystyle {\overline {{{P}_{0}}{{P}_{2}}}}}$;${\displaystyle {P}''(1)=0}$ اگر و تنها اگر ${\displaystyle {{P}_{2}}}$نقطهٔ میانی المان${\displaystyle {\overline {{{P}_{1}}{{P}_{3}}}}}$ باشد. نمونه‌هایی در شکل ۳ نشان داده شده‌است.

چسباندن دو منحنی بی زی ای

۱-مطابقت دادن نقاط انتهایی

شکل ۴

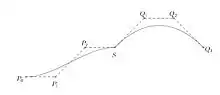
با دو منحنی که می‌توانند به همدیگر بچسبند ولی با یکدیگر به خوبی مطابقت ندارند شروع می‌کنیم. منحنی اول با نقاط کنترلی${\displaystyle {{\text{P}}_{0}}{\text{ }}{{\text{P}}_{1}}{\text{ }}{{\text{P}}_{2}}{\text{ }}{{\text{P}}_{3}}}$ و منحنی دوم دارای نقاط کنترلی${\displaystyle {{Q}_{0}}{\text{ }}{{\text{Q}}_{1}}{\text{ }}{{\text{Q}}_{2}}{\text{ }}{{\text{Q}}_{3}}}$. همان‌طور که در شکل ۴ نشان داده شده‌است. فرض کنید که${\displaystyle {{\text{Q}}_{0}}={{\text{P}}_{3}}}$، برای قرارداد این نقطهٔ اتصال را s می‌نامیم،${\displaystyle {{\text{Q}}_{0}}={{\text{P}}_{3}}=s}$نتیجه در شکل ۴ نمایش داده شده‌است. منحنی دارای یک گوشه است، زیرا در s منحنی بی زی ای اول دارای مشتق اول${\displaystyle {\text{3(S-}}{{\text{P}}_{2}}{\text{)}}}$ است و منحنی دوم${\displaystyle {\text{3(}}{{\text{Q}}_{1}}{\text{-S)}}}$، ولی بردارهای ${\displaystyle S-{\text{ }}{{\text{P}}_{2}}}$ و ${\displaystyle {{\text{Q}}_{1}}{\text{-S}}}$ حتی دارای یک جهت نیز نیستند.

۲-مطابقت دادن اندازه‌ها و مشتقات اول

یک اتصال بهتر زمانی بدست می‌آید که s نقطه میانی خط P2Q1 باشد، به طوری که مشتق اول در محل اتصال مطابقت داشته باشد. شکل۵ نمونه‌ای است که دارای این شرایط می‌باشد. این نمونه هموارتر به نظر می‌آید. با این وجود، هنوز آرمانی نمی‌باشد. فرض کنید سوار بر قطاری هستید که روی این منحنی حرکت می‌کند. در بخش اول منحی بی زی ای به سمت دیواری سمت چپ فشار داده می‌شوید و در بخش دیگر به سمت مخالف یعنی دیوار سمت راست فشرده می‌شوید. در نقطهٔ اتصال شما از سمتی به سمت دیگر قطار کشیده می‌شوید. برای اتصالی هموارتر، انحنا می‌بایستی پیوسته باشد. چون که انحنا را می‌توان در قالب مشتقات اول و دوم بیان کرد، پیوستگی انحنا را می‌توان با مطابقت دادن مشتقات اول و دوم در نقطهٔ اتصال بدست آورد. ۳-مطابقت دادن اندازه، مشتق اول و دوم در s، با قرار دادن t=1 , t=۰ …مشتق دوم منحنی بی زی ای به صورت 6(p1-2p2+s) و 6(s-2q1+q2) می‌شود. بنابراین داریم: 6(p1-2p2+s)=6(s-2q1+q2) ویا متعاقباً p1-p2=q2-2q1. راهی جالب برای درون یابی از این معادله. دو طرف را در منفی ضرب می‌کنیم تا داشته باشیم: 2p2-p1=2q1-q2. علت انجام این کار این است که هر دو طرف دارای ضرایبی با اختلاف یک هستند و بنابراین نقاطی را ارائه می‌دهند که از دستگاه مختصات مستقل اند. طرف سمت چپ به نقطهی A+ می‌انجامد و از p1 و p2 می‌گذرد. در حقیقت

A+=2p2-p1=p2+1.(p2-p1). همانگونه که در شکل ۶ نشان داده شده‌است. A+ را راس زائیهٔ راست از چند ضلعی کنترلی اول می‌نامیم. به صورتی مشابه، بخش سمت راست معادله را راس زاویه‌ای سمت چپ نامیده و برابر است با

A-=2q1-q2 از منحنی بی زی ای دوم، مطابق شکل. همانگونه که می‌بینید، در این مثال دو راس زاویه‌ای یکسان نیستند، بنابراین معادله ارضا نمی‌شود و مشتقات دوم از منحنی‌های بی زی ای با یکدیگر مطابق نخواهند بود. شکل ۷ مثالی را نشان می‌دهد که این مطابقت ایجاد شده‌است، در حالی که هر دو راس زاویه‌ای در نقطهٔ یکسان A قرار دارند. قسمت مذکور در شکل ۷ به مشابه یک کلمهٔ A می‌باشد که به آن کابین با قاب A گویند. تعریف: قاب-Aشکلی است با نقاط نشان داده شده، به گونه‌ای که s نضطهٔ میانی p2p1، و p2 نقطهٔ میانیp1A، وq1 نقطهٔ میانی Q2A. مثالی در شکل ۸ آورده شده‌است؛ بنابراین: اگر دو منحنی بی زی ای در نقطهٔ s متصل شوند، هر دو مشتق اول و دوم در s مطابقت خواهند داشت اگر و تنها اگر چند ضلعی کنترلی آنها قاب_A را تشکیل دهند. نکته: مطابقت دادن مشتقات سوم اگر چه اطمینان بخش می‌باشد، ولی مفید نیست، همانگونه که هر دو منحنی را مجبور می‌کند که بخشی از یک منحنی درجه سوم باشند؛ بنابراین انعطاف‌پذیری بدست آمده ناشی از چسبانده دو منحنی از بین می‌رود.

منابع

http://www.math.ucla.edu/~baker/149.1.02w/handouts/x_lagrange.pdf بایگانی‌شده در ۱۰ مارس ۲۰۱۲ توسط Wayback Machine http://www.math.ucla.edu/~baker/149.1.02w/handouts/bb_bezier.pdf بایگانی‌شده در ۱۰ مارس ۲۰۱۲ توسط Wayback Machine http://www.math.ucla.edu/~baker/149.1.02w/handouts/dd_splines.pdf