الگوریتم حل هزارتو
تعداد متفاوتی الگوریتم برای حل مسئلهٔ مارپیچ وجود دارد که آنها، روشهای خودکاری برای حل مارپیچها هستند. الگوریتمهای موشی تصادفی، دنبال کنندهٔ دیوار، تضمینی و الگوریتم تریماکس برای این طراحی شدهاند که درون مارپیچ و توسط سیاری استفاده شوند که هیچ دانش قبلی نسبت به توپولوژی مارپیچ ندارد، در حالی که پر کردن بن بست و الگوریتمهای کوتاهترین راه برای این طراحی شدهاند که به وسیلهٔ شخص یا برنامهٔ رایانهای که میتواند در لحظه کل مارپیچ را ببیند، استفاده شوند. مارپیچهایی که هیچ حلقهای ندارد به مارپیچهای استاندارد یا کامل شناخته میشوند و با مفهوم درخت در نظریهٔ نظریه گرافها هم ارزهستند. به همین دلیل بسیاری از الگوریتمهای حل مارپیچ به نظریهٔ گراف مربوط هستند. به طوری که اگر کسی مسیرهای مارپیچ را در جهت درست بکشد، نتیجهٔ حاصل میتواند تبدیل به یک درخت شود.[1]
الگوریتم موشی تصادفی
این یک روش بدیهی برای این مسئله است که توسط یک روبات غیر هوشمند یا شاید یک موش میتواند پیادهسازی شود و آن به سادگی حرکت کردن در یک مسیر مستقیم تا رسیدن به یک تقاطع است و بعد انتخاب یک مسیر به صورت تصادفی است تا در آن جهت حرکت شود. گرچه چنین روشی همواره در نهایت به یک پاسخ درست میرسد، اما این الگوریتم میتواند بسیار کند باشد.
دنبال کننده دیوار
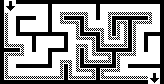

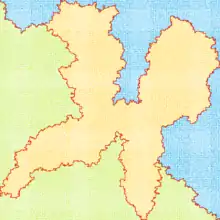
دنبال کنندهٔ دیوار، معروفترین قاعده در طی کردن مارپیچ است که به آن قاعدهٔ دست چپ یا قاعدهٔ دست راست نیز میگویند. اگر مارپیچ یک فضای همبند ساده باشد، یعنی تمام دیوارهایش به هم یا به دیوارهٔ خارجی مارپیچ متصل باشند، با گرفتن یک دست به یک دیوار مارپیچ تضمین میشود که بازیکننده گم نمیشود و اگر که خروجی وجود داشته باشد به خروجی میرسد؛ در غیر این صورت، او دوباره به ورودی بازمیگردد در حالی که هر تونل مارپیچ را حداقل یک بار طی کرده باشد. یک دیدگاه دیگر برای این که چرا دنبال کنندهٔ دیوار نتیجه میدهد، دیدگاه توپولوژی است. اگر دیوارها متصل باشند، ممکن است به صورت یک حلقه یا دایره تغییر شکل دهند آنگاه دنبال کردن دیوار به حرکت کردن دور دایره از نقطهٔ آغاز تا پایان خلاصه میشود. برای پیشبرد این ایده ملاحظه شود که با گروه کردن مؤلفههای همبند دیوارهای مارپیچ، مرزهای آنها بهطور دقیق همان جواب هستند، حتی اگر بیش از یک جواب وجود داشته باشد. (شکلهای سمت راست) اگر مارپیچ پیوستهٔ ساده نباشد (یعنی اگر نقطهٔ شروع یا نقاط پایان در مرکز ساختار مارپیچ باشد یا مسیرها از رو یا زیر هم بگذرند.) این روش تضمینی ندارد که در رسیدن به هدف کمک کند. دنبال کردن دیوار میتواند در مارپیچهای سه بعدی یا با بعدهای بیش تر انجام شود اگر امکانش باشد که به صورت قطعی مسیرهای آن روی صفحهٔ ۲بعدی تصویر شود. برای مثال در یک مارپیچ ۳ بعدی میتوان مسیرهایی که به سمت خارج میآیند را به سمت شمال غربی و مسیرهایی که به داخل میروند را به سمت شمال شرقی در نظر بگیریم.
الگوریتم تضمین کننده

مارپیچهای نا پیوسته را نیز میتوان با الگوریتم دنبالکننده دیوار حل کرد به شرط اینکه درگاههای ورود و خروج در دیواره بیرونی مارپیچ قرار داشته باشند. اما اگر بهطور مثال نقطه شروع در داخل صفحه باشد، ممکن است در یک بخش جدا از بخش خروجی باشد ؛ در این صورت تعقیبکننده دیوار بهطور دائمی به دور خود خواهد گشت. الگوریتم تضمینی (به نام Jon Pledge این نامگذاری شدهاست) این مشکل را حل خواهد کرد. الگوریتم تضمینی طوری طراحی شدهاست که موانع احتمالی را رفع میکند و نیازمند انتخاب یک جهت دلخواه حرکت است . هنگامی که یک مانع دیده میشود یک دست را (برای مثال دست راست) بهطور ثابت به دیواره مانع گرفته و حرکت میکنیم و به ازای تمام چرخشها زاویهٔ چرخش را به مجموع زوایای چرخش اضافه میکنیم و هنگامی که به جهت حرکت اولیه بازگشتیم و مجموع زوایای چرخش صفر شد، یعنی مانع را دور زدهایم و مسیر را ادامه میدهیم. در این الگوریتم هنگامی دست را از دیوار برمیداریم که مجموع زوایای چرخش و جهت فعلی(نسبت به جهت اولیه) برابر صفر شده باشد. این کار این امکان را به الگوریتم میدهد که در مسیرهای تله دار به شکل حرف "G" گیر نیفتد. فرض کنید که الگوریتم(در حرکت روی G) از دیوار اولی به سمت چپ بپییچد آنگاه به وسیلهٔ دیوارها مجبور میشود۳۶۰ درجه بچرخد. الگوریتمی که تنها جهت فعلی را دنبال کند در حلقه بینهایت میافتد. این چنین که هنگامی که راستترین دیوار پایین را ترک کند، دوباره وارد بخش منحنی سمت چپ میشود. الگوریتم تضمینکننده راستترین دیوار را به دلیل اینکه مجموع زوایای چرخش در آن نقطه صفر نشده، ترک نمیکند و دیوار را همچنان دنبال میکند تا در نهایت با حرکت به سمت چپ و دقیقاً زیر شکل حرف از آن خارج میشود. ین الگوریتم به یک فرد به همراه قطب نما این امکان را میدهد که از هر نقطه درونی، بدون در نظر گرفتن مکان اولیه، به یک خروجی در بیرون هر مارپیچ متناهی دوبعدی راه یابد. اما قابلیت یافتن مسیر برای حالاتی که نقطه شروع خارج صفحه و نقطه پایان داخل صفحه باشد را دارا نیست.
الگوریتم تریماکس
الگوریتم تریماکس که توسط چارلز پیر ترماکس معرفی شده، یک روش بهینه برای پیدا کردن راه خروجی مارپیچ است که لازمهٔ آن کشیدن خطهایی روی زمین است که مسیری را مشخص کند و تضمین شدهاست که برای تمام مارپیچهایی که مسیرهای خوش تعریفی دارند کار میکند. یک مسیر یا هنوز بازدید نشده یا یک بار علامت زده شده یا دو بار. هر بار مسیری انتخاب میشود با زدن علامت روی زمین (از انشعاب تا انشعاب) مشخص میشود. از ابتدا یک مسیر اتفاقی انتخاب میشود (اگر بیش از یک مسیر وجود داشته باشد) در هنگام رسیدن به انشعابی که هنوز بازدید نشده (هیچ مسیر علامت داری نیست) یک مسیر اتفاقی انتخاب میشود (و مسیر را علامتگذاری میکنیم). در هنگام رسیدن به انشعاب علامت دار، اگر مسیر کنونی یک علامته باشد مسیر رفته را برمیگردیم (و مسیر بازگشت را برای بار دوم علامت گذاری میکنیم) اگر این حالت نبود مسیری که کمترین علامت دارد را انتخاب میکنیم (و طبق معمول آن را علامت گذاری میکنیم)، وقتی بالاخره به نتیجه رسیدیم مسیرهایی که دقیقاً یک بار علامت گذاری شدهاند یک مسیر مشخص به شروع را نشان میدهند. اگر خروجی وجود نداشته باشد، این روش، مسیر را تا شروع نشان میدهددر حالی که تمام مسیرها دو علامته هستند. در این حالت هر مسیر دقیقاً دو بار طی میشود، در هر جهت یک بار. نتیجهٔ این حرکت ردیابی ۲طرفه نام دارد. این الگوریتم در حقیقت نوعی از الگوریتم جستجوی عمق اول است.[2][3]
الگوریتم پر کردن بنبست

پرکردن بن بستها الگوریتمی است برای حل مارپیچها که در آن تمام مسیرهای بنبست غیر از مسیر درست پر میشود. برای مواقعی که مارپیچ بر روی کاغذ است یا توسط رایانه قصد حل آن را از این روش میتوان استفاده کرد . در این الگوریتم تمام صفحه مارپیچ یکجا دیده میشود بنابراین برای فردی که داخل یک مارپیچ نامعلوم قرار دارد مفید نمیتواند باشد . روش کلی کار این است که اول تمام بن بستها را پیدا کرده و سپس از یک بن بست تا اولین انشعاب را پر میکند. ویدئوی اجرای عملی این روش در اینجا قابل مشاهده است .ویدیو در یوتیوبویدیو در یوتیوب. الگوریتم پرکردن بنبست نمیتواند بهطور اتفاقی یک مسیر را از ابتدا حذف کند و باید برای تمام بن بستها اجرا شود زیرا در هر مرحله توپولوژی مارپیچ حفظ میشود. علاوه برآن، این رویه به دلیل اینکه پاسخ نهایی نمیتواند هیچ بنبستی را شامل شود طولانی!!!! خواهد بود . اگر این الگوریتم بر روی مارپیچی کامل (مارپیچی که دور نداشته باشد) اجرا شود، جوابی یکتا خواهد داد اما در صورت وجود دور تنها میتواند مسیرهای احتمالی مسئله را به ما بدهد.
الگوریتم کوتاهترین مسیر
هنگامی که یک مارپیچ چند راه حل داشته باشد، ممکن است حلکننده بخواهد کوتاهترین مسیر از ابتدا تا انتها را پیدا کند. یک الگوریتم ممکن کوتاهترین مسیر را با پیادهسازی الگوریتم جستجوی اول سطح پیدا میکند. در حالی که الگوریتمی دیگر، الگوریتم جستجوی آ*، از روشهای اکتشافی استفاده میکند. الگوریتم جستجوی سطح اول از یک صف استفاده میکند که خانهها را به ترتیب بر اساس فاصلهٔ آنها از ابتدا تا انتها بازدید میکند. هر خانهٔ بازدید شده باید اطلاعات مربوط به فاصلهٔ خودش از نقطهٔ شروع یا اینکه کدام یک از همسایگانش که به شروع نزدیک تر است باعث شده که به صف اضافه شود را نگه دارد. هنگامی که مکان انتهایی پیدا شود مسیر خانهها بازمیگردیم تا به نقطهٔ شروع برسیم که این مسیر کوتاهترین مسیر است
مطالب بیش تر
- Mazes
- Maze_generation_algorithm
- Stop_or_My_Dog_Will_Shoot جلسه از از سریال سیمپسونها که در آن لیسا سیمپسون از الگوریتم تریماکس استفاده میکند.
منابع
- مشارکتکنندگان ویکیپدیا. «Maze solving algorithm». در دانشنامهٔ ویکیپدیای انگلیسی.
- Abelson; diSessa (1980), Turtle Geometry: the computer as a medium for exploring mathematics
- Public conference, December 2, 2010 - by professor Jean Pelletier-Thibert in Académie de Mâcon (Burgundy - France) - (Abstract published in the Annals academic, March 2011)
Charles Tremaux (° 1859 - † 1882) École Polytechnique de Paris (X:1876), French engineer of the telegraph
- Édouard Lucas: Récréations Mathématiques Volume I, 1882.
- H. Fleischner: Eulerian Graphs and related Topics. In: Annals of Discrete Mathematics No. 50 Part 1 Volume 2, 1991, page X20.
پیوند به بیرون
- Maze to Tree - YouTube در یوتیوب
- Even, Shimon (2011), Graph Algorithms (2nd ed.), Cambridge University Press, pp. 46–48, ISBN 9780521736534.
- Sedgewick, Robert (2002), Algorithms in C++: Graph Algorithms (3rd ed.), Pearson Education, ISBN 9780201361186.