بازی آخرین پیشنهاد
بازی آخرین پیشنهاد یک مثال از بازیهای دونفرهٔ نوبتی است که در نظریه بازیها بررسی میشود. در این بازی به نفر اول میزانی پول داده میشود، او پیشنهاد میدهد این پول را چگونه بین خودش و نفر دوم تقسیم کنید. نفر دوم تصمیم میگیرد که این تقسیمبندی را قبول دارد یا نه. اگر قبول کند پول بینشان به نسبتی که نفر اول پیشنهاد داده تقسیم میشود. در غیر این صورت به هر دو هیچ پولی نمیرسد.
تعریف ریاضی و بررسی تعادلها
از اینجا به نفر اول «پیشنهاد دهنده» و به نفر دوم «بررسی کننده» میگوییم. فرم نوبتی بازی به این صورت تعریف میشود:
- به پیشنهاد دهنده ۱ واحد پول داده میشود.
- پیشنهاد دهنده انتخاب میکند که پارامتر پیشنهادی او برای تقسیم پول است، که در صورت قبول واحد به پیشنهاد دهنده و واحد به بررسیکننده پول میرسد.
- بررسیکننده پیشنهاد را بررسی میکند، اگر پیشنهاد را بپذیرد پول به نسبتی که در پیشنهاد آمده بینشان تقسیم میشود، در غیر این صورت به هیچکدام پولی نمیرسد.
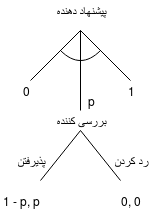
در بازی نوبتی، اگر فرض کنیم کمترین مقدار مثبتی مانند وجود دارد که پول موجود کمتر از آن تقسیم نمیشود، بازی یک تعادل کامل زیربازی خواهد داشت. اگر پیشنهاد دهنده را به عنوان پارامتر تقسیم انتخاب کند، نفر دوم بین مقدار مثبت در حالت پذیرفتن و در حالت رد کردن را ترجیح میدهد، همانطور که در مثل فارسی داریم: «کاچی به از هیچی». با فرض گرفتن این رفتار بررسی کننده، پیشنهاد دهنده برای بیشینه کردن سود خودش پارامتر تقسیم را برابر قرار میدهد. این شیوهٔ بازی کردن تعادل کامل زیربازی در این بازی است.[1]
اگر بازی را همزمان در نظر بگیریم، به این صورت که پیشنهاد دهنده پارامتر را انتخاب میکند و بررسیکننده پارامتر را انتخاب میکند و تنها در صورتی پیشنهاد را میپذیرد که باشد. در این صورت هر وضعیت استراتژی که در آن باشد یک تعادل است. همینطور اگر باشد در هیچ حالتی به پیشنهاد دهنده پولی نمیرسد پس تمام انتخابهای برای پیشنهاد دهنده یک نقطهٔ تعادل است.
در واقعیت
هر چند اگر بازیکنان تماماً منطقی و با هدف بیشینه کردن سود خود بازی کنند، پیشنهاد دهنده باید بیشترین مقداری که میتواند را ذخیره کند و تنها مقدار مثبت کمی پول برای بررسیکننده در نظر بگیرد. اما اگر این بازی را در واقعیت انجام دهیم این رفتار را نمیبینیم. در واقع هم پیشنهاد دهنده تقسیم عادلانهتری پیشنهاد میکند و هم بررسیکننده بعضی پیشنهادهایی که مقدار مثبت ولی کمی برایش در نظر گرفته شده را نمیپذیرد. بررسیکننده با این کار به ناعادلانه بودن تقسیم اعتراض میکند.
اگر این آزمایش را در کشورهای مختلف انجام دهیم بسته به فرهنگ جامعه، نتایج مختلفی مشاهده میکنیم. بهطور مثال در یک آزمایش مشاهده شدهاست بیشتر بازیکنان پیشنهاد دهنده بین ۴۰ تا ۵۰ درصد پول را به نفر دوم پیشنهاد میدهند و حدود نیمی از بازیکنان بررسیکننده پیشنهادهای کمتر از ۳۰ درصدی را رد میکنند.[2]
این مشاهدات نشان میدهد که انسانها با مفهومی به نام عدالت آشنایی دارند. احتمال درک عدالت در سایر حیوانات نیز وجود دارد. در تحقیقی که روی میمونها انجام شد به تعدادی از آنها آموخته شد که میتوانند سنگریزه را با خیار معاوضه کنند. در این حالت اگر میمونی متوجه شود که هم نوعش با پرداخت سنگریزه میوه بهتری مثلاً انگور بدست میآورد، اعتصاب میکند و سنگریزهاش را با خیار معاوضه نمیکند هر چند که داشتن خیار از داشتن سنگریزه برایش سود بیشتری دارد.[3]
تفسیر رفتار
تأکید غیرمنطقی انسانها بر تقسیم منصفانه نشان میدهد که ترجیح انسانها صرفاً به میزان سود شخصیشان وابسته نیست و برای تنبیه پیشنهاد دهندگانی که میزان کمی پول به آنها میدهند، پیشنهاد را رد میکنند. یکی از توجیهات این رفتار میتواند این باشد که انسانها احتمال میدهند که دوباره با هم برخورد کنند.
توجیه دیگر میتواند مربوط به مدل کردن سود هر کس باشد. برای مثال فرض کنید در بازی تقسیم ۱۰۰ دلار، میزان نارضایتی نفر دوم در صورتی که x دلار بگیرد که این میزان کمتر از ۵۰ دلار است، باشد. در این صورت سود او از دریافت x دلار اگر باشد برابر با و در غیر این صورت برابر با است. در این حالت منطقی است که نفر دوم پیشنهادهای بالای ۴۰ دلار را بپذیرد، زیر ۴۰ دلار را رد کند و پذیرفتن یا رد کردن ۴۰ دلار برایش تفاوتی نداشته باشد.[4]
در بازار
این بازی را در نظر بگیرید. فروشنده قصد دارد روی محصولش قیمتگذاری کند. فرض میکنیم ساخت محصول هزینهای برای فروشنده نداشته باشد. یعنی اگر محصول را با قیمت بفروشد واحد سود میکند. از طرف دیگر خریدار برای محصول ارزشی برابر در نظر دارد و تنها در صورتی محصول را میخرد که قیمت آن از کمتر باشد که سود کند. در صورتی که این بازی، بازی با اطلاعات کامل باشد، فروشنده میتواند با قرار دادن قیمت کمی کمتر از ارزش محصول، بیشترین سود را بکند. این بازی نوعی از بازی پیشنهاد آخر است که در بازار دیده میشود.[5]
بررسی از دید نظریه تکاملی بازیها
برای مدل کردن بازی فرض کنید مجموع آنچه قرار است تقسیم شود برابر با ۱ واحد است و هر بازیکن به احتمال یکسان در یکی از دو جایگاه پیشنهاد دهنده و یا بررسیکننده قرار میگیرد. استراتژی هر کس را برابر قرار میدهیم که هر دو اعدادی در بازه [۰٬۱] هستند. برابر با میزانی است که اگر بازیکن در جایگاه پیشنهاد دهنده قرار گیرد پیشنهاد میدهد و اگر در جایگاه بررسیکننده قرار گیرد هر میزان پیشنهاد کمتر از را رد میکند.
حال اگر این مدل را سادهتر کنیم به بازی کوچک یا minigame میرسیم. در این حالت تنها دو پیشنهاد و (کم و زیاد) وجود دارد به طوری که . پس هر بازیکن تنها ۴ استراتژی ، ، و دارد که به ترتیب با ... نمایش میدهیم. استراتژی منطقی پیشنهاد میزان کمی پول و قبول هر میزانی پول میباشد که در حقیقت تنها تعادل کامل زیربازی میباشد. مقدار زیادی پیشنهاد میدهد ولی با مقدار کم نیز موافقت میکند. استراتژی عادلانه ایست که میزان زیادی پیشنهاد میکند و با میزان زیادی هم موافقت مینماید و میزان کمی پیشنهاد میدهد و با میزان بالایی پول موافقت میکند.
در بررسی این بازی از دید نظریه تکاملی بازیها، اگر در ابتدا با جمعیتی روبهرو باشیم که شامل افراد با ۴ استراتژی گفته شدهاست، در نهایت پس از مدتی که این جمعیت بازی را بین خود انجام میدهند تنها گونهای که بقا پیدا میکند است. در واقع در نهایت تمامی افراد جامعه خواهند بود.[2]
| G4 | G3 | G2 | G1 | |
| l | h | 1 | G1 | |
| 1 | 1 | G2 | ||
| 1 | 1 | G3 | ||
| 0 | h | G4 |
منابع
- Easley, D. and Kleinberg, J. , 2010. Networks, crowds, and markets. Cambridge Univ Press, 6(1), pp.1-6.
- Nowak, M.A. , Page, K.M. and Sigmund, K. , 2000. Fairness versus reason in the ultimatum game. Science, 289(5485), pp.1773-1775.
- T.N. Sherratt and D.M. Wilkinson, Cooperation and Sociality, In Encyclopedia of Animal Behavior, edited by Michael D. Breed and Janice Moore, Academic Press, Oxford, 2010, Pages 396-401, ISBN 978-0-08-045337-8
- Schecter, Steve, and Herbert Gintis. "Introduction to Game Theory."
- Nisan, N. , Roughgarden, T. , Tardos, E. and Vazirani, V.V. eds. , 2007. Algorithmic game theory (Vol. 1). Cambridge: Cambridge University Press.