بطری کلاین
فلیکس کلاین، ریاضیدان آلمانی و عضو آکادمی علوم برلین در سال ۱۸۸۲ نمونه جالبی از سطح یک رویه طرح کرد که به بطری کلاین معروف شدهاست. این بطری سطح کاملاً بستهای دارد. با وجود این، برای آن نمیتوان رویه داخلی یا خارجی معلوم کرد و به عبارتی دیگر حجم آن صفر است. این شکل هم مثل نوار موبیوس داری یک رویه است ولی بر خلاف آن هیچ کنارهای ندارد. میتوان برشی از آن بدست آورد که هر نیمه آن یک نوار موبیوس تشکیل دهد.

نوار موبیوس که توسط آگوست فردیناند موبیوس، ریاضیدان و ستارهشناس مشهور آلمانی کشف شد نیز، حالت خاصی از بطری کلاین به حساب میآید.
بطری کلاین و نوار موبیوس در نظریات در کیهان شناسی
در کیهان شناسی مطرح شدهاست که کیهان را به شکل زین اسب میداند و اشکالی نیز به نام بطری کلاین و نوار موبیوس ارائه شدهاست. در بطری کلاین جهان بسته است و به شکل یک بطری است در نوار موبیوس جهان درون و بیرون ندارد، اگر حرکت در جهان را از جایی شروع کنیم که روی نوار باشد که سرانجام از زیر نوار سر درمی آوریم یا اگر از زیر آن شروع کنیم به روی آن خواهیم آمد.
خانه بطری کلاین را میتوان یکی از بزرگترین آثار معماری معاصر دانست که از خاصیت بطری کلاین در طراحی آن استفاده شدهاست.
توپولوژی و بطری کلاین
در صحبت از توپولوژی معمولاً اشیایی مانند نوار موبیوس، بطری کلاین، گرهها و حلقهها نخستین چیزهایی هستند که به ذهن میآیند. اما برخی با عبارتی طنزآمیز توپولوژیستها را توصیف میکنند؛ آنها میگویند توپولوژیست کسی است که فرقی میان فنجان قهوه و پیراشکی نمیبیند! در تعریف بطری کلاین نیز، سطح داخلی و خارجی معنا ندارد و تعریف نمیشود، در حقیقت فرقی میان سطح داخلی و خارجی این بطری نیست![1]
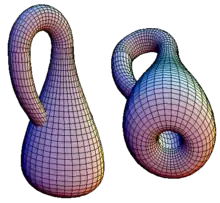
از ادغام دو، سه یا چند بطری کلاین میتوان بطری کلاینهای دوبله، سوبله و... را به وجود آورد.(مطابق شکلهای روبرو:


جستارهای وابسته
منابع
- مشارکتکنندگان ویکیپدیا. «Klein bottle». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۰ ژانویه ۲۰۱۳.