تابع درخشندگی

منحنی حساسیت چشم، یک تابع یا منحنی است که میانگین حساسیت چشم انسان‌ها به نور را در طول موجهای مختلف مشخص می‌کند. باید توجه داشت که این منحنی کاملاً دقیق نیست، اما نمایش بسیار خوبی از حساسیت چشم انسان است. این تابع یک تابع استاندارد است که توسط سی‌آی‌ئی معرفی شده و می‌توان از آن برای تبدیل انرژی تابشی به انرژی نورانی (که رویت‌پذیر است) استفاده کرد. همچنین این تابع اساس کار تابع تطبیق رنگ در فضای رنگ ۱۹۳۱ سی‌آی‌ئی است.

توابع درخشندگی در دید کافی (مشکی) و در شب‌بینی (سبز).[c 1] منحنی دید کافی استاندارد ۱۹۳۱ سی‌آی‌ئی را نیز شامل می‌شود[c 2] (خط پیوسته)، داده‌های تغییریافتهٔ جاد-ووس در ۱۹۷۸ میلادی[c 3] (خط‌چین)، داده‌های شارپ، استاک‌من، جاگلا و جاگل در ۲۰۰۵ میلادی[c 4] (نقطه‌چین). منحنی افقی طول موج بر حسب نانومتر است.

جزئیات

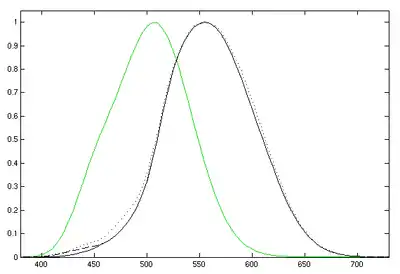
دو تابع درخشندگی داریم که کاربرد بیشتری دارند. برای سطح نورهای روز، تابع درخشندگی دید کافی دارای بهترین تقریب برای پاسخ‌دهی چشم انسان است. برای سطح نورهای پایین، پاسخ‌دهی چشم انسان تغییر می‌کند و منحنی شب‌بینی به کار می‌رود. منحنی دید کافی همان منحنی استاندارد سی‌آی‌ئی است که در فضای رنگ ۱۹۳۱ سی‌آی‌ئی استفاده شد.

شار نوری یک چشمهٔ نور را با استفاده از تابع درخشندگی دید کافی تعریف می‌کنند. معادلهٔ زیر برای محاسبهٔ شار نوری کل یک چشمهٔ نور به کار می‌رود:

${\displaystyle F=683.002\ \mathrm {lm/W} \cdot \int _{0}^{\infty }{\overline {y}}(\lambda )J(\lambda )d\lambda }$

که در آن

${\displaystyle F\,}$ شار نوری بر حسب لومن است

${\displaystyle J(\lambda )\,}$ توزیع توان طیفی تابش است (توان در واحد طول موج)، بر حسب وات بر متر

${\displaystyle {\overline {y}}(\lambda )}$ (که با ${\displaystyle V(\lambda )\,}$ هم نمایش می‌دهند)، تابع استاندارد درخشندگی است که بعد ندارد

${\displaystyle \lambda \,}$ طول موج بر حسب متر است.

به‌طور رسمی این انتگرال به صورت ضرب داخلی تابع درخشندگی در طیف نور تعریف می‌شود.[1] در عمل اما، به جای انتگرال از جمع‌زدن روی بازه‌هایی گسسته از طول موج که در جداول تابع درخشندگی وجود دارند استفاده می‌شود. سی‌آی‌ئی جدول‌های استاندارد تابع درخشندگی را در فاصله‌های 5 nm از 380 nm تا 780 nm توزیع می‌کند.[cie 1]

تابع استاندارد درخشندگی در مقدار بیشینهٔ خود در ۵۵۵ نانومتر نرمال‌سازی می‌شود (ضریب نوری را ببینید). مقدار ثابت جلوی انتگرال را معمولاً به ۶۸۳ لومن بر وات گرد می‌کنند. مقدار مازاد این کسر، از ناهمخوانی جزئی بین تعریف لومن و بیشینهٔ تابع درخشندگی ناشی می‌شود. لومن به گونه‌ای تعریف شده تا یکای انرژی تابشی ۱/۶۸۳ وات در فرکانس ۵۴۰ تراهرتز باشد که معادل است با طول موج هوایی استاندارد ۵۵۵٫۰۱۶ نانومتر (که با ۵۵۵ نانومتر که بیشینهٔ منحنی درخشندگی است برابر نیست). مقدار ${\displaystyle {\overline {y}}(\lambda )}$ در ۵۵۵٫۰۶ نانومتر ۰٫۹۹۹۹۹۷ است، بنابراین مقدار ۶۸۳/۰٫۹۹۹۹۹۷ = ۶۸۳٫۰۰۲ ضریب تناسب خواهد بود.[2] عدد ۶۸۳ به تعریف نوین کاندلا (یکای شدت نور در ۱۹۷۹ میلادی) وابسته‌است.[cie 2] این عددِ دلبخواه باعث شد در تعریف جدید، عددهایی برابر عددهای تعریف قدیمی کاندلا بدست آید.

بهبوددادن‌های استاندارد

تابع درخشندگی دید کافی سی‌آی‌ئی ۱۹۲۴${\displaystyle V(\lambda )}$،[cie 3] که در تابع تطبیق رنگ سی‌آی‌ئی ۱۹۳۱ به صورت y درآمده، مدت‌ها بود که بخاطر دست کم گرفتن اثرِ انتهایِ آبیِ طیف، در نور دریافتی، شناخته‌شده بود. تلاش‌های زیادی برای بهبود استاندارد تابع صورت گرفته تا نمایندهٔ بهتری از چشم انسان باشد. از جملهٔ این تلاش‌ها می‌توان به کار جاد[3] در سال ۱۹۵۱ میلادی[4] و کار ووس[5] در سال ۱۹۷۸ میلادی اشاره کرد[6] که منجر به تابعی به نام سی‌آی‌ئی ${\displaystyle V_{M}(\lambda )}$.[7] شد. پس از آن، شارپ، استاک‌من، جاگلا و جاگل در سال ۲۰۰۵ میلادی تابعی را که با اصول مخروط استاکمن و شارپ[8] سازگار بود گسترش دادند. این منحنی در نمودار بالای این صفحه رسم شده‌است.

درخشندگی شب‌بینی

برای شدت نورهای بسیار پایین (شب‌بینی)، حساسیت چشم به جای سلول‌های مخروطی به سلول‌های میله‌ای وابسته است و منحنی به سمت بنفش جابجا می‌شود، به‌طوری‌که بیشینهٔ آن در حدود ۵۰۷ نانومتر برای چشم جوانان قرار می‌گیرد. در این بیشینه، حساسیت برابر است با ۱۶۹۹[9] یا ۱۷۰۰[10] لومن بر وات.

تابع درخشندگی استاندارد شب‌بینی یا ${\displaystyle V^{\prime }(\lambda )}$ در سال ۱۹۵۱ میلادی در سی‌آی‌ئی به کار گرفته شد که بر پایهٔ اندازه‌گیری‌های والد[11] (۱۹۴۵ میلادی) و کرافورد (۱۹۴۹ میلادی) بود.[12]

جستارهای وابسته

• دید رنگی
• بازده کوانتوم، معادل حسگر تصویر

منابع

• Wikipedia contributors, "Luminosity function," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Luminosity_function&oldid=480772576 (accessed March 23, 2012).

1. Charles A. Poynton (2003). Digital Video and HDTV: Algorithms and Interfaces. Morgan Kaufmann. ISBN 1558607927.
2. Wyszecki, Günter and Stiles, W.S. (2000). Color Science - Concepts and Methods, Quantitative Data and Formulae (2nd ed.). Wiley-Interscience. ISBN 0-471-39918-3.
3. Judd
4. Judd, Deane B. and Wyszecki, Günter (1975). Color in Business, Science and Industry (3rd ed.). John Wiley. ISBN 0-471-45212-2.
5. Vos
6. Vos, J. J. (1978). "Colorimetric and photometric properties of a 2° fundamental observer". Color Research and Application. ۳ (۳): ۱۲۵–۱۲۸. doi:10.1002/col.5080030309.
7. Stiles, W. S.; Burch, J. M. (1955). "Interim report to the Commission Internationale de l'Eclairage Zurich 1955, on the National Physical Laboratory's investigation of colour-matching". Optica Acta. ۲ (۴): ۱۶۸–۱۸۱. Bibcode:1955AcOpt...2..168S. doi:10.1080/713821039.
8. Sharpe, L. T.; Stockman, A.; Jagla, W.; Jägle, H. (2005). "A luminous efficiency function, V*(λ), for daylight adaptation" (PDF). Journal of Vision. ۵ (۱۱): ۹۴۸–۹۶۸. doi:10.1167/5.11.3. Archived from the original (PDF) on 26 April 2012. Retrieved 23 March 2012.
9. Kohei Narisada; Duco Schreuder (2004). Light Pollution Handbook. Springer. ISBN 140202665X.
10. Casimer DeCusatis (1998). Handbook of Applied Photometry. Springer. ISBN 1563964163.
11. Wald
12. Scotopic luminosity function

سندهای سی‌آی‌ئی

1. "CIE Free Documents for Download".
2. 16th Conférence générale des poids et mesures Resolution 3, CR, 100 (1979), and Metrologia, 16, 56 (1980).
3. CIE (1926). Commission internationale de l'Eclairage proceedings, 1924. Cambridge University Press, Cambridge.

داده‌های منحنی

1. "CIE Scotopic luminosity curve (1951)". Archived from the original on 28 December 2008. Retrieved 23 March 2012.
2. "CIE (1931) 2-deg color matching functions". Archived from the original on 28 December 2008. Retrieved 23 March 2012.
3. "Judd-Vos modified CIE 2-deg photopic luminosity curve (1978)". Archived from the original on 28 December 2008. Retrieved 23 March 2012.
4. "Sharpe, Stockman, Jagla & Jägle (2005) 2-deg V*(l) luminous efficiency function". Archived from the original on 27 September 2007. Retrieved 23 March 2012.