توابع جزء صحیح و سقف
در ریاضیات و علوم کامپیوتر دو تابع «جزء صحیح یا کف (یا براکت)» و «سقف» توابعی هستند که به ترتیب هر مقدار حقیقی که به آنها داده شود را به بزرگترین عدد صحیح کوچکتر (یا مساوی) و کوچکترین عدد صحیح بزرگتر (یا مساوی) گرد میکنند. به عبارت دیگر تابع جزء صحیح که به صورت نمایش داده میشود به بزرگترین عدد صحیح قبل از آن گرد میکند یعنی به طور مثال ۲٫۶ را به ۲ و ۳٫۴- را به ۴- گرد میکند اما تابع سقف که به صورت نمایش داده میشود به کوچکترین عدد صحیح بعد از آن گرد میکند یعنی ۲٫۶ را به ۳ و ۳٫۴- را به ۳- گرد میکند.[1]
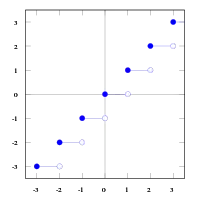
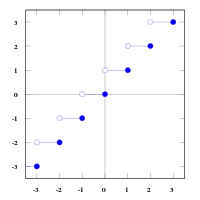
نماد گزینی
گاوس ریاضیدان آلمانی، نماد براکت گوشهدار [ ] را در اثبات قانون تقابل درجه دوم برای نمایش «تابع جزءِ صحیح» معرفی نمود (سال ۱۸۰۸ میلادی) که تا ارائهٔ نماد جدید کنت ای آیورسن به صورت استاندارد استفاده میشد. کنت ای آیورسن اصطلاحات «کف» و «سقف» را با نمادگذاری به صورت و در کتاب زبان برنامهنویسیاش ارائه نمود (سال ۱۹۹۶). گرچه استاندارد نمادگذاری مطابق با نمادگذاری «آیورسن» است اما در ریاضیات امروزی از هر دو نمادگذاری استفاده میگردد.[2]
اتحادهای جزء صحیح
تعریف ریاضیاتی جزء صحیح به شرح زیر است:
شکست در تجزیه (پاسخ نامعتبر MathML همراه SVG یا PNG جایگزین (توصیه شده برای مرورگرهای مدرن و ابزارهای کمکی) ("Math extension cannot connect to Restbase.") از سرور "/mathoid/local/v1/":): {\displaystyle \lfloor x\rfloor=max \{ n\in\Zeta'| n\leq x\}}
معنی آن به زبان عامیانه این است: جزء صحیح X بیشترین عدد صحیحی است که کمتر یا مساوی X است.
بعضی مواقع جزء صحیح یک عدد را به صورت [x] هم نشان میدهند.
آنگاه
If:z<x<y➡[x]=z
یعنی هرگاه xبین z و y باشد جزء صحیح آن برابر مقدار کوچک تر(z) است
مثال:
x=1.9999➡[x]=1
x=1.00001 ➡[x]=1
x=-1.01➡ [x]=-2
x=-1.99➡ [x]=-2
برخی از اتحادهای معروف:
A)
.
.
B) ===== ==> هر عددی از یک جزء صحیح و یک جزء کسری تشکیل شده است.
.
.
C)
منابع
- Graham, Knuth, & Patashnik, Ch. 3.1
- ویکیپدیای انگلیسی
- Wikipedia contributors, "Floor and ceiling functions," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Floor_and_ceiling_functions&oldid=448721821 (accessed October 21, 2011).