حرف مفت

در نظریه بازی، حرف مفت یک نوع برقراری ارتباط بین بازیکن‌ها است که به طور مستقیم بر روی سود آنها اثر ندارد. فرستادن و دریافت اطلاعات بدون هزینه است. این وجه تفاوت حرف مفت با بازی علامت‌دهی است که در آن فرستادن پیام‌های مختلف برای فرستنده هزینه‌بر است و مقدار آن به حالت دنیا بستگی دارد.

یک بازیکن دارای اطلاعات است و بازیکن دیگر توانایی عمل دارد. بازیکن مطلع می‌تواند به صورت استراتژیک انتخاب کند که چه بگوید و چه نگوید. اوضاع وقتی جالب‌تر می‌شود که منافع دو بازیکن با یکدیگر تفاوت داشته باشد. مثال کلاسیک این مسئله یک کارشناس (مثلاً یک بوم‌شناس) است که تلاش دارد تا وضعیت جهان را به گونه‌ای به تصمیم‌گیرنده نامطلع (مثلاً سیاست‌مداری که در مورد لایحه جنگل‌زدایی رای می‌دهد) توضیح دهد. تصمیم‌گیرنده پس از شنیدن گزارش کارشناس، باید یک تصمیم بگیرد که به طور غیرمستقیم سود هر دو بازیکن را تحت تأثیر قرار می‌دهد.

مدل مقدماتی این بازی توسط کراوفورد و سوبل مطرح شد و بعدها انواع مختلفی از آن ارائه گردید.

تعریف رسمی ارتباط حرف مفت به صورت زیر است:[1]

۱. ارسال و دریافت پیام بدون هزینه است.

2. محدودکننده نیست. (یعنی انتخاب استراتژیک هیچ‌کدام از طرفین را محدود نمی‌کند)

3. قابل اثبات نیست. (یعنی صحت اطلاعات توسط یک نفر سوم مثل دادگاه قابل تأیید نیست)

در نتیجه یک نفر درگیر در حرف مفت می‌تواند با خیال راحت از پیگرد دروغ بگوید؛ اما ممکن است در تعادل چنین تصمیمی نگیرد.

مقاله اصلی کراوفورد و سوبل

نحوه بازی

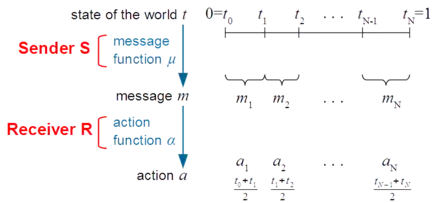
در شکل مقدماتی بازی، دو بازیکن با یکدیگر ارتباط برقرار می‌کنند که یکی فرستنده S و دیگری گیرنده R است.

نوع: فرستنده از حالت دنیا یا نوع خودش t آگاهی دارد. گیرنده t را نمی‌داند. او تنها یک باور قبلی در مورد آن دارد و با توجه به پیام فرستاده شده توسط فرستنده سعی دارد که دقت باور خود را در صورت امکان افزایش دهد.

پیام: فرستنده تصمیم می‌گیرد که پیام m را بفرستد. پیام m ممکن است اطلاعات کامل را دربرداشته باشد، اما این امکان هم وجود دارد که اطلاعات محدودی و مبهمی داشته باشد؛ مثلاً بگوید که «حالت دنیا بین t1 و t2 است.» همچنین این امکان هم وجود دارد که پیام دارای هیچ گونه اطلاعاتی نباشد.

شکل پیام، تا زمانی که درک مشترکی بین دو بازیکن وجود داشته باشد، اهمیتی ندارد. می‌تواند یک بیانیه کلی از رئیس کل بانک مرکزی، صحبت یک سیاست‌مدار و … باشد. هر شکلی که این پیام داشته باشد، در نهایت به صورت " حالت دنیا بین t₁ و t_{2 است}" درمی‌آید.

عمل: گیرنده پیام m را دریافت می‌کند و به وسیله آن و به وسیله قاعده بیز، باورش نسبت به حالت دنیا را به‌روز می‌نماید. R تصمیم می‌گیرد که عمل a را انجام دهد. این عمل هم بر مطلوبیت خودش و هم بر مطلوبیت فرستنده اثرگذار خواهد بود.

مطلوبیت: تصمیم S در مورد محتوای پیام m بر اساس حداکثرسازی مطلوبیت خودش، با فرض دانستن آنچه که R انجام می‌دهد است. مطلوبیت یک روش برای عددی کردن میزان رضایت و تمایلات است و می‌تواند به صورت سود مالی، یا رضایت غیرمالی باشد. مثلاً این که طبیعت چقدر مورد محافظت قرار گرفته است.

مطلوبیت‌های به فرم درجه دوم:

مطلوبیت S و R به ترتیب به صورت زیر مشخص می‌شود:

$${\displaystyle U^{S}(a,t)=-(a-t-b)^{2}}$$

$${\displaystyle U^{R}(a,t)=-(a-t)^{2}}$$

در تئوری فرم کلی‌تری را در نظر گرفته می‌شود، اما ترجیحات درجه دوم تفسیر را راحت‌تر می‌کند. اگر b≠۰ باشد، S و R اهداف مختلفی خواهند داشت. تفسیر پارامتر b میزان تضاد منافع دو بازیکن است.

U^R وقتی حداکثر می‌شود که a=t باشد، یعنی گیرنده تمایل دارد که عملی را انجام دهد که با حالت جهان (که در حالت کلی آن را نمی‌داند) مطابق باشد U^S زمانی حداکثر می‌شود که a=t + b باشد. به این معنی که S تمایل دارد یک عمل a بزرگتر انجام شود. از آنجایی که S نمی‌تواند عمل را کنترل کند، برای رسیدن به عمل دلخواه خود باید تصمیم بگیرد که چه پیامی را منتقل کند. مطلوبیت هرکدام از بازیکن‌ها به حالت جهان و تصمیم مشترک آنها که در نهایت به عمل a منجر می‌شود بستگی دارد.

تعادل نش : ما تعادلی را بررسی می‌کنیم که هر بازیکن با فرض رفتار بهینه طرف مقابل، به صورت بهینه رفتار می‌کند. بازیکن‌ها عقلایی هستند، هرچند R دارای اطلاعات محدود است. انتظارات تحقق پیدا می‌کنند و انگیزه‌ای برای تخطی از این وضعیت وجود ندارد.

قضیه

شکل ۱: نحوه ارتباط در بازی حرف مفت

کراوفورد و سوبل خواص تعادل‌های نش ممکن را مشخص کرده‌اند.

• در حالت کلی چند تعادل نش وجود دارد؛ اما تعداد آنها محدود است.
• تعادل جداکننده، به معنای انتقال کامل اطلاعات توسط فرستنده وجود ندارد.
• تعادل سخن بیهوده که به معنای عدم انتقال هرگونه اطلاعات توسط فرستنده است، همواره یک خروجی تعادلی است.
  

زمانی که منافع کاملاً هماهنگ باشد، اطلاعات به صورت کامل منتقل می‌شود. زمانی که تضاد منافع بسیار بزرگ باشد، هیچ اطلاعاتی منتقل نمی‌شود. این دو حالت، حالت‌های افراطی مسئله هستند. حالت جالب‌تر زمانی است که منافع به هم نزدیک ولی متفاوت هستند. در این حالت رفتار بهینه انتقال بخشی از اطلاعات (و نه همه آن) خواهد بود.

به طور کلی:

• وجود دارد ${\displaystyle N^{*}>0}$ به طوری که به ازای هر ${\displaystyle N}$ که ${\displaystyle 1\leq N\leq N^{*}}$ ،
• حداقل یک تعادل وجود دارد که در آن، ${\displaystyle N}$ عمل مختلف می‌تواند انجام شود و به علاوه،
• هیچ تعادلی وجود ندارد که بیش از ${\displaystyle N^{*}}$ عمل را در پی داشته باشد.
  

پیام‌ها: در حالی که به صورت پیشینی می‌توان بی‌نهایت پیام با مقادیر مختلف و به ازای حالت‌های مختلف جهان t فرستاد، اما در واقعیت تنها تعداد محدودی پیام با مقادیر ${\displaystyle (m_{1},m_{2},..,m_{N})}$ می‌توان ارسال نمود.

در نتیجه تعادل ممکن است توسط یک افراز ${\displaystyle (t_{0}(N),t_{1}(N),...,t_{N}(N))}$ از مجموعه نوع‌های ${\displaystyle [0,1]}$ ، که در آن ${\displaystyle 0=t_{0}(N)<t_{1}(N)<...<t_{N}(N)=1}$ مشخص شود. این افراز در بخش بالا و راست شکل ۱ نشان داده شده است.

${\displaystyle t_{i}(N)}$ها مرزهای بازه‌هایی هستند که به ازای آنها فرستنده یک پیام ثابت را ارسال می‌کند. یعنی به ازای هر ${\displaystyle t_{i-1}<t<t_{i}}$، خواهیم داشت ${\displaystyle \mu (t)=m_{i}}$.

عمل‌ها: از آنجایی که عمل‌ها توابعی از پیام‌ها هستند، آنها نیز روی این بازه‌ها ثابت هستند. یعنی برای ${\displaystyle t_{i-1}<t<t_{i}}$ باید ${\displaystyle a(t)=a(m_{i})=a_{i}}$

تابع عمل، مقداری از ${\displaystyle a}$ است که سود انتظاری گیرنده را حداکثر کند، به شرطی که بداند t بین ${\displaystyle t_{1}}$ و ${\displaystyle t_{2}}$ است. با فرض توزیع یکنواخت t بین صفر و یک، بیان ریاضی مسئله به صورت زیر می‌شود:

${\displaystyle a_{i}={\bar {a}}(t_{i-1},t_{i})=\mathrm {arg} \max _{a}\int _{t_{i-1}}^{t_{i}}U^{R}(a,t)dt}$

${\displaystyle \leftarrow }$تابع مطلوبیت‌های درجه دوم:

به شرطی که R بداند که t بین ${\displaystyle t_{1}}$ و ${\displaystyle t_{2}}$ است و در حالت خاص تابع مطلوبیت درجه دوم، برای انتخاب a به طوری که تا حد امکان به t نزدیک باشد، R باید وسط بازه مورد نظر باشد (این موضوع را به صورت شهودی می‌توان نشان داد):${\displaystyle a_{i}={\frac {t_{i-1}+t_{i}}{2}}}$

شرط بی‌تفاوتی: اگر t = ti باشد چه می‌شود؟ فرستنده باید بین فرستادن دو پیام ${\displaystyle m_{i-1}}$ و ${\displaystyle m_{i}}$ بی‌تفاوت باشد. یعنی:

${\displaystyle U^{S}(a_{i},t_{i})=U^{S}(a_{i+1},t_{i})}$ به ازای هر ${\displaystyle 1\leq i\leq N-1}$

این شرط به ما اطلاعاتی در مورد N و ${\displaystyle t_{i}}$ می‌دهد.

در عمل:

افرازی به اندازه N را در نظر می‌گیریم.

می‌توان نشان داد که:

${\displaystyle t_{i}=t_{1}i+2bi(i-1)\qquad t_{1}={\frac {1-2bN(N-1)}{N}}}$

N باید به قدر کافی کوچک باشد تا صورت کسر مثبت شود. این شرط حداکثر مقدار قابل قبول N را مشخص می‌کند:

${\displaystyle N^{*}=\langle {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {1+{\frac {2}{b}}}}\rangle }$

که 〈Z〉 سقف عدد Z و به معنای کوچکترین عدد بزرگتر یا مساوی Z می‌باشد.

مثال: با فرض b=۱/۲۰، خواهیم داشت ۳=*N.

اکنون تمام تعادل‌ها را به ازای N=۱٬۲٬۳ بررسی می‌کنیم (شکل ۲ را ببینید).

شکل ۲: پیام‌ها و مطلوبیت‌ها به ازای میزان تضاد منافع b=۱/۲۰ و به ازای N=1,2,3

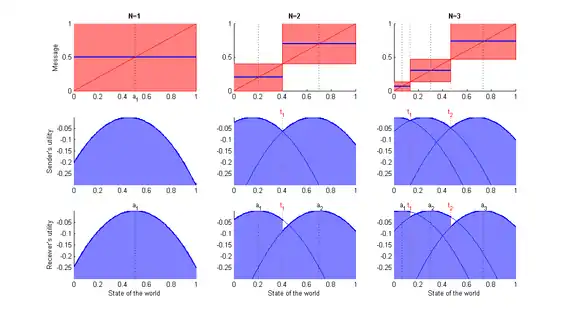
N = ۱:این یک تعادل سخن بیهوده است. t₀ = 0, t₁ = 1; a₁ = ۱/۲ = 0.5.

N = ۲: در این حالت: t₀ = 0, t₁ = ۲/۵ = 0.4, t₂ = 1; a₁ = ۱/۵ = 0.2, a₂ = ۷/۱۰ = 0.7.

N = N^* = ۳: در این صورت: t₀ = 0, t₁ = 2/15, t₂ = 7/15, t₃ = 1; a₁ = 1/15, a₂ = ۳/۱۰ = 0.3, a₃ = 11/15.

به ازای N=۱، بی‌فایده‌ترین تعادل را داریم که در آن هیچ اطلاعاتی منتقل نمی‌شود. در نتیجه تمام شکل در پنل سمت راست به رنگ قرمز درآمده است. به ازای N=۳، وضعیت پیام‌رسانی بهتر است. اما همچنان نسبت به حالت انتقال کامل اطلاعات بسیار ناجذاب است. (حالت انتقال کامل اطلاعات که با خط ۴۵ درجه نشان داده شده است، یک تعادل نش نیست)

به ازای Nهای بزرگ‌تر و در نتیجه ارسال پیام باکیفیت‌تر، سطوح آبی اهمیت بیشتری پیدا می‌کند که به معنای افزایش مطلوبیت است. انتقال اطلاعات بیشتر باعث سود بیشتر هر دو طرف می‌شود.

کاربردها

نظریه بازی

حرف مفت، در حالت کلی می‌تواند به هر بازی اضافه شود و مجموعه خروجی‌های تعادلی بازی را متنوع‌تر کند. برای مثال، می‌توان یک دور حرف مفت را به ابتدای بازی نزاع همسران اضافه کرد. هر بازیکن در ابتدا اعلام می‌کند که دوست دارد به مسابقه فوتبال یا به اپرا برود. چون نبرد جنسیت‌ها یک بازی هماهنگی است، یک برقراری ارتباط در ابتدای بازی می‌تواند باعث شود که بازیکن‌ها بین چند تعادل یکی را انتخاب کنند و در نتیجه به سود بیشتری نسبت به حالت بدون هماهنگی دست پیدا کنند. پیام و عملی که به این خروجی منجر می‌شود، برای هر بازیکن متقارن است. یعنی: ۱) اپرا یا فوتبال را با احتمال مساوی اعلام کنند. ۲) اگر یک نفر اپرا (یا فوتبال) را اعلام کرد، با شنیدن این پیام نفر دوم هم اپرا (یا فوتبال) را انتخاب خواهد کرد. (فرل و رابین، ۱۹۹۶) اگر دو بازیکن گزینه‌های مختلفی را انتخاب کنند، هماهنگی شکل نمی‌گیرد. در صورتی که تنها یک بازیکن پیام دهد، این بازیکن دارای مزیت خواهد بود.

البته تضمینی وجود ندارد که حرف مفت باعث اثرگذاری روی خروجی و سود بازیکنان شود. مثلاً در بازی تعارض زندانی‌ها، که تنها تعادل آن در اتخاذ استراتژی‌های غالب است. در این بازی هرگونه ارتباط قبل از بازی، اهمیت ندارد و بازیکن‌ها فارغ از هر گونه پیام ارسال شده فقط استراتژی‌های غالب خود (نقض همکاری، نقض همکاری) را بازی خواهند کرد.

زیست‌شناسی

این که حرف مفت اثری بر روی ساختار بازی اصلی ندارد، بسیار مورد مخالفت واقع شده است. در زیست‌شناسی، استدلال شده است که فرستادن پیام با هزینه به بهترین نحو پیام‌دهی را در بین حیوانات توضیح می‌دهد. (نقض اصل و نظریه علامت‌دهی را ببینید) این باور عمومی با چالش‌هایی روبرو شده است (کارهای انجام شده توسط کارل برگشتروم و برایان اسکرمز را ببینید). به خصوص مدل‌های متعددی با استفاده از نظریه بازی تکاملی نشان می‌دهند که حرف مفت می‌تواند بر روی دینامیک تکاملی برخی بازی‌های خاص اثر بگذارد.

جستارهای وابسته

• نظریه بازی‌ها
• بازی علامت‌دهی

یادداشت

1. Farrell, Joseph (1987). "Cheap Talk, Coordination, and Entry". The RAND Journal of Economics. 18 (1): 34–39. JSTOR 2555533.

منابع

• Crawford, V. P.; Sobel, J. (1982). "Strategic Information Transmission". Econometrica. 50 (6): 1431–1451. doi:10.2307/1913390.