درجه آزادی (مکانیک)
تعداد پارامترهای غیر وابسته که برای مشخص کردن موقعیت یک سیستم فیزیکی مورد استفاده قرار میگیرد را درجه آزادی آن سیستم مینامند.
به عنوان مثال یک ذره نقطهای که در فضا آزادانه حرکت میکند دارای سه درجه آزادی است. همان ذره اگر در یک صفحه به صورت آزادانه حرکت کند دارای دو درجه آزادی خواهد بود. در واقع تعداد درجه آزادی یک سیستم همواره با تعداد بعدهایی که سیستم در آن حرکت میکند برابر است. حال اگر سیستم فیزیکی از نوع ذرهای نباشد، مشخص کردن موقعیت تنها یک نقطه از آن جسم، برای مشخص کردن موقعیت سیستم کافی نخواهد بود.
برای روشن شدن بهتر مطلب به مثالهای زیر توجه کنید.
۱- محاسبه درجه آزادی یک سیستم فیزیکی که از N ذره (که به صورت آزادانه و غیر وابسته نسبت به یکدیگر میتوانند در فضا حرکت کنند) برابر است با:3N، برای واضح کردن پاسخ تنها کافی است که با کمی تأمل مشاهده کنیم که سیستم از N ذره تشکیل شده است و هر ذره نسبت به دیگری حرکتی غیر وابسته دارد و از آنجا که میدانیم یک ذره در فضا دارای ۳ درجه آزادی است (به عنوان مثال در دستگاه مختصات کارتزین ۳ درجه آزادی ذره برابر خواهد بود با حرکت در راستای سه محور X,Y,Z) پس کافی است که عدد ۳ را در تعداد ذرات ضرب کرده و درجه آزادی کل سیستم را بیابیم.
۲- محاسبه درجه آزادی یک میله صلب به طول L (یک سیستم مادهای) که آزادانه در فضا حرکت میکند (از ضخامت و عرض صرف نظر کنید) برابر است با: ۵. اگر میله را به مانند یک خط مد نظر بگیرید و آن را به عنوان مثال در در دستگاه مختصات کارتزین قرار دهیم میتوانیم دو نقطه را به صورت دلخواه انتخاب کنیم. برای راحتی دو نقطه ابتدایی و انتهایی میله را در نظر بگیریم و نقطهها را a,b بنامیم. این دو نقطه دارای مختصات Xa,Ya,Za و Xb,Yb,Zb خواهند بود. اما به راحتی میتوان فهمید که این ۶ مختصات از یکدیگر غیر وابسته نیستند و به سادگی رابطه وابستگی آنها را میتوان دریافت.
(L=√((Xb- Xa)²+(Yb- Ya)² +(Zb- Za)²
رابطه بالا به سادگی نشان میدهد یکی از ۶ پارامتر وابسته به ۵ پارامتر دیگر است، در نتیجه درجه آزادی برابر ۵ است. راه دیگر برای رسیدن به عدد ۵ استفاده از رابطه کسینوسی است که به سادگی میتوان دریافت که ۶ پارامتر غیر وابسته نیستند.
۳- محاسبه درجه آزادی یک جسم صلب که در فضا آزادانه حرکت می کند برابر است با:۶. که در مختصات دستگاه کارتزین برابر است با ۳ حرکت در راستای X,Y,Z و سه چرخش در حول سه محور X,Y,Z
۴- درجه آزادی یک ذره نقطهای که در صفحه بر روی یک مسیر دایرهای با شعاع R حرکت میکند برابر است با: ۱
همانطور که میدانید در دایره مختصات X,Y به یکدیگر وابسته هستند تنها کافی است بدانیم کهX²+Y²=R² پس به سادگی درمییابیم که این ذره دارای ۱ درجه آزادی است و همانطور هم که در بالا گفته شد این بار تعداد درجه آزادی با تعداد بعدهایی که سیستم در آن حرکت میکند (صفحه = دو بعد) برابر نیست.
در واقع درجات آزادی برابر است با تعداد مجهولاتی که می توان با آن معادله مربوط را حل کرد.
سیستم یک درجه آزادی
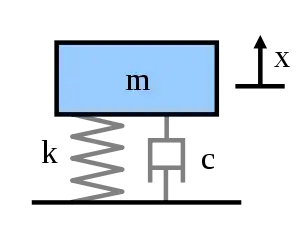
سیستم یک درجه آزادی اصطلاحا به سیستمی گفته میشود که فقط و فقط دارای آزادی حرکت در یک درجه آزادی است. این سیستم متشکل از سه پارامتر اصلی جرم M و میرایی C و سختی K است. امکان دارد سیستم یک درجه آزادی با میرایی صفر وجود داشته باشد. در بحثهای مربوط به دینامیک سازهها اساس کار بر رفتار سیستم یک درجه آزادی استوار است و پاسخ سیستم چند درجه آزادی بر همین اساس بدست میآید.
منابع
(FISICA 1- (Mencuccini-Silvestrini
(MECCANICA RAZIONALE (ENZO OLIVIERI