درخت ۲–۳-۴
در علوم کامپیوتر، درخت 2-3-4(که به آن درخت 2-4 هم گفته میشود) داده ساختاری است که عموماً برای پیادهسازی فهرست ها(لیست ها) استفاده میشوند. عدد هر گره نشانگر تعداد فرزندان گره است که میتواند دو، سه یا چهار گره باشند :
- گره-2، یک مقدار و دو گره فرزند دارد
درخت 2-3-4
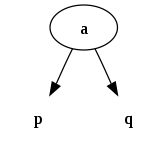
- گره-3، دو مقدار و سه گره فرزند دارد
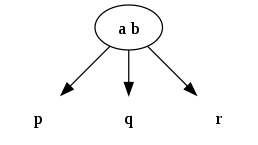
- گره-4، سه مقدار و چهار گره فرزند دارد
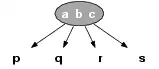
درختهای 2-3-4 درخت باینری مرتبه 4 هستند و مانند درخت باینری می توانند عملیات جستجو، درج کردن و حذف کردن را در زمان (O(log n انجام دهند. یک خاصیت این درخت این است که تمامی برگها (پایینترین گره که فرزند هم ندارد) در یک ارتفاع هستند . درخت های 2-3-4 و درخت های قرمز-سیاه یک به یک هستند، به این معنا که برای هر درخت 2-3-4 فقط یک درخت قرمز-سیاه وجود دارد . عملیات درج کردن و حذف کردن روی درخت 2-3-4 موجب گسترش، جـدا شدن و ادغام گره ها میشود که معادل تعویض رنگ و جابجایی گره ها در درخت قـرمز-سیاه است . برای آشنایی با درخت قـرمز-سیاه معــمولا در ابتــدا درخت 2-3-4 معرفی میشود، چرا که در مفهوم آسانتر است. اما بدلیل حالتهای خاص در انجام عملیات روی درخت 2-3-4 پیادهسازی این درخت در بسیاری از زبانهای برنامه نویسی مشکل است. چون پیادهسازی درخت قرمز-سیاه آسانتر است به درخت 2-3-4 ترجیح داده میشود .
خواص
- هر گره، یک گره-2 یا گره-3 یا گره-4 است که به ترتیب شامل یک، دو، سه مقدار میشود.
- تمامی برگها در یک ارتفاع قرار میگیرند.
- تمامی داده ها ترتیب عددی دارند.
درج کردن
برای درج یک عدد از ریشه شروع می کنیم .
1 . اگر گروه گره -4 بود :
- مقدار وسط را حذف می کنیم تا تبدیل به گره -3 شود.
- دو مقدار گره -3 را در دو گروه جداگانه قرار می دهیم.
- اگر گره مورد نظر ریشه بود :
- مقدار وسط تبدیل ریشه جدید گره -2 میشود و ارتفاع درخت عدد یک افزوده میشود.
- در غیر این صورت مقدار وسطی (حذف شده) به گره پدر منتقل میشود .
2 . فرزندی را پیدا می کنیم که بتواند شامل عدد مورد نظر شود .
3 . اگر فرزند فرزندی نداشت عدد را به همان گره اضافه می کنیم .
- در غیر اینصورت به سراغ فرزند می رویم و همین کار را تکرار می کنیم .
حذف کردن
برای حذف کردن یک عنصر از درخت 2-3-4 1 . عنصر مورد نظر را پیدا می کنیم
- اگر عنصر برگ نبود، با توجه به مکانش جستجو را تا رسیدن به یک برگ ادامه میدهیم. این برگ میتواند بزرگترین مقدار کوچکتر از عنصر مورد نظر یا کوچکترین مقدار بزرگتر از آن باشد. آسانترین راه این است که تعدیلی در درخت انجام دهیم. به این صورت پس از بیرون انداختن یک عنصر هیچ برگ خالی نخواهیم داشت.
- اگر عنصر رد برگ گره-2 قرار داشت به روش زیر عمل می کنیم :
- 1 . اگر برادری (گره هم ارتفاع) داشت که گره-3 یا گره-4 بود، یک جابجای(چرخش) انجام می دهیم.
- نزدیک ترین کلید گره برادر به عنصر مورد نظر را به گره بالاتری که پدر هر دو باشد انتقال می دهیم.
- کلید گره پدر را به گره پایین(که می خواهیم عنصر را از آن حذف کنیم) انتقال می دهیم.
- عنصر مورد نظر اکنون فرزندی اضافی است.
- 2 . اگر پدر و برادر هم گره-2 بودند، سه گره را ادغام و درخت را کوتاه می کنیم.
- 3 . اگر پدر گره-3 یا گره-4 و تمامی برادرها گره-2 بودند، عمل ادغام را با پدر و برادر مجاور انجام می دهیم.
- برادر مجاور و پدر می توانند یک گره-4 باشند.
- فرزندان برادر را به این گره منتقل می کنیم.
هنگامی که به عنصر مورد نظر رسیدیم، می توانیم آن را حذف کنیم جرا که تضمین کرده ایم که گره برگ بیش از یک کلید دارد. عملیات حذف کردن در درخت 2-3-4 از مرتبه (O(log n است، با فرض انجام جابجایی و ادغام در (O(1 .
منابع
- Knuth, Donald (1998), Sorting and Searching, هنر برنامهنویسی رایانه, Volume 3 (Second ed.), Addison-Wesley, ISBN 0-201-89685-0. Section 6.2.4: Multiway Trees, pp. 481–491. Also, pp. 476–477 of section 6.2.3 (Balanced Trees) discusses 2-3 trees.