رمزنگاری هیل

وجود شاخص‌های آماری برای دو یا سه حرفی‌ها، لستر اس.هیل را به این فکر واداشت که بایستی بیش از سه حرف را در هم ادغام کرد تا بلکه استحکام بیشتریدر مقابل حملات مبتنی بر شاخص‌های آماری متن، به وجود بیاید. این ریاضی دان از جبر ماتریسی بهره گرفت : الف) هر حرف انگلیسی به ترتیب با عددی صحیح بین 0 تا 25(A=0; B=1; C=2; ...) جایگزین می‌شود. ب) متن در قالب گروهای n حرفی به n حرف جدید نگاشته می‌شوند. الگوی تبدیل با روابط خطی زیر توصیف می‌شود : ${\displaystyle =\sum _{i=0}^{n-1}\ K_{1i}.P_{i}mod26}$

ماشین رمزنگاری هیل

${\displaystyle =\sum _{i=0}^{n-1}\ K_{2i}.P_{i}mod26}$

${\displaystyle =\sum _{n=0}^{n-1}\ K_{ni}.P_{i}mod26}$

می‌توان روابط بالا را به صورت ماتریسی نشان داد :

${\displaystyle C=(K.P)mod26}$

که در آن Pو C دو بردار n*1 و K ماتریسی n*n است. در رمز ((هیل)) کلید رمز در حقیقت همین ماتریس K است. برای مثال فرض کنید کلید رمز به صورت زیر فرض شده باشد. ماتریس K

${\displaystyle {\begin{pmatrix}6&24&1\\13&16&10\\20&17&15\end{pmatrix}}}$

ماتریس کلید نشان می‌دهد که متن باید به صورت سه حرفی رمز شود. فرض کنید بخواهیم کلمه "ACT" را رمز کنیم :

${\displaystyle {\begin{pmatrix}0\\2\\19\end{pmatrix}}}$

با این پارامترها، نتیجه رمز هیل به صورت زیر بدست خواهد آمد :

${\displaystyle {\begin{pmatrix}6&24&1\\13&16&10\\20&17&15\end{pmatrix}}{\begin{pmatrix}0\\2\\19\end{pmatrix}}={\begin{pmatrix}67\\222\\319\end{pmatrix}}\equiv {\begin{pmatrix}15\\14\\7\end{pmatrix}}{\pmod {26}}}$

بدین ترتیب سه حرفی ACT به سه حرفی POH تبدیل می‌شود. در رمزنگاری هیل هر چه طول گروه‌های n حرفی افزایش یابد، امنیت روش بهبود خواهد یافت ولی در عوض کلید رمز که همان ماتریس K بشدت بزرگ شده و راهی جز یادداشت کردن آن باقی نخواهد ماند که بر خلاف اصول ششگانه کرکهف، امنیت را به گونه دیگری به مخاطره خواهد افکند.

در مجموع روش هیل به حمله مبتنی بر متن شناخته شده حساس است چرا که کاملاً خطی است و با داشتن تعداد کافی متن اصلی و معادل رمز شده می‌توان به کلید رمز دست یافت.

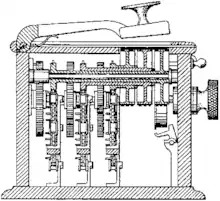
شخص آقای هیل و شریکش برای رمزنگاری و رمزگشایی متون، ماشینی مکانیکی را طراحی و به عنوان اختراع در سند US-Patent 1,845,947 به ثبت رساندند! این ماشین که شمای آن را مشاهده می‌کنید حروف متن را در دسته‌های شش حرفی، ادغام و رمزنگاری می‌کرد و کلاً از چرخ دنده و زنجیر و تسمه ساخته می‌شد و از لحاظ ظاهر به چرخ خیاطی شباهت داشت ولی هیچکس سفارش خرید چنین ماشینی را نداد!

رمزگشایی ((هیل)) دقیقاً همانند فرایند رمزنگاری است با این تفاوت که به جای ماتریس K وارون آن (یعنی ${\displaystyle K^{-1}}$ به پیمانه 26) بکار می‌رود. با ضرب ${\displaystyle K^{-1}.C}$ داده‌ها از رمز خارج شده و P بدست می‌آید. بدیهی است که در انتخاب K باید دقت شود تا دترمینان آن صفر نبوده و K وارون پذیر باشد.

منابع

• "Hill Cipher Deciphered" provides an excellent explanation of computing matrix inverses with regard to the Hill cipher.
• Lester S. Hill, Cryptography in an Algebraic Alphabet, The American Mathematical Monthly 36, June-July ۱۹۲۹ (میلادی), pp306–312.
• Lester S. Hill, Concerning Certain Linear Transformation Apparatus of Cryptography, The American Mathematical Monthly 38, ۱۹۳۱ (میلادی), pp135–154.
• Jeffrey Overbey, William Traves, and Jerzy Wojdylo, On the Keyspace of the Hill Cipher, Cryptologia, 29(1), January 2005, pp59–72. (PDF)
• Shahrokh Saeednia, How to Make the Hill Cipher Secure, Cryptologia, 24(4), October 2000, pp353–360.