زبان منظم

در علوم نظری رایانه، زبان‌های منظم، به زیرمجموعه‌ای از زبان‌های صوری گفته می‌شود.

Chomsky-hierarchy

اعضای یک زبان منظم با عبارت‌های منظم ساخته‌می‌شوند و توسط ماشین حالت متناهی معین پذیرفته می‌شوند. از زبان‌های منظم در تجزیه کننده‌ها و طراحی زبان‌های برنامه‌نویسی استفاده می‌شود.

تعریف

مجموعهٔ زبان‌های منظم روی یک الفبا مثل ${\displaystyle \Sigma }$، به صورت بازگشتی زیر تعریف می‌شود:

• زبان بدون رشته،${\displaystyle \emptyset }$، یک زبان منظم است.
• برای هر عضو الفبا، ${\displaystyle a\in \Sigma }$، مجموعهٔ تک‌عضوی ${\displaystyle \{a\}}$، یک زبان منظم است.
• اگر مجموعه‌های ${\displaystyle A}$ و ${\displaystyle B}$ دو زبان منظم باشند، آنگاه اجتماع آن‌ها ${\displaystyle (A\cup B)}$، الحاق آن‌ها ${\displaystyle (A\cap B)}$ وستاره کلین (${\displaystyle A^{*}}$) زبان‌های منظم هستند.

مثال

هر مجموعه‌ای شامل تعداد متناهی رشته یک زبان منظم است. مجوعهٔ تک‌عضوی شامل رشتهٔ تهی، ${\displaystyle \{\epsilon \}}$ یک زبان منظم است. به همین‌ترتیب، روی الفبای ${\displaystyle \{a,b\}^{*}}$، زبانی که شامل تعداد برابر از حروف ${\displaystyle a}$ و ${\displaystyle b}$ باشد، یک زبان منظم است.

${\displaystyle \{a^{n}b^{n}|n\geq 0\}}$ یک زبان منظم نیست. یعنی این زبان، زبان مورد پذیرش برای هیچ ماشین حالت متناهی نیست و نمی‌توان آن را با عبارت‌های منظم بیان کرد. برای نشان دادن آن که یک زبان، منظم نیست، از لم تزریق، استفاده می‌شود.

بیان‌های دیگر

یک زبان منظم:

• زبان مورد پذیرش یک اتوماتون تعین‌ناپذیر متناهی، (NFA) است.
• زبان مورد پذیرش یک ماشین‌های تعین‌پذیر حالات متناهی، (DFA) است.
• زبان مورد پذیرش یک یک ماشین حالت متناهی متناوب، (AFA) است.
• توسط یک دستور منظم (Regular grammar)، ساخته‌می‌شود.
• توسط یک دستور پیشوندی (Prefix grammar)، ساخته‌می‌شود.
• زبان مورد پذیرش یک ماشین تورینگ است.
• قابل بیان در منطق مرتبهٔ دوم است.

تساوی‌های جبری برای عبارت‌های منظم

• ${\displaystyle (R^{*})^{*}=R^{*}}$
• ${\displaystyle (\epsilon +R)^{*}=R^{*}}$
• ${\displaystyle R+R^{*}=R^{*}}$
• ${\displaystyle RR^{*}=R^{+}}$

ویژگی‌های بستاری

اگر زبان‌های M و N، منظم باشند:

• اجتماع دو زبان، یعنی ${\displaystyle M\cup N}$ منظم است.
• الحاق آن دو، ${\displaystyle M\circ N}$ منظم است.
• اشتراک آن‌ها، یعنی ${\displaystyle M{\hat {N}}}$ منظم است.
• ستاره کلین هر کدام از آن‌ها، ${\displaystyle M^{*}}$ و ${\displaystyle N^{*}}$ منظم‌اند.
• تفریق و متمم آن‌ها،${\displaystyle M-N}$ و ${\displaystyle {\bar {M}}}$ منظم‌اند.
• معکوس زبان، ${\displaystyle M^{R}}$، منظم است.

ویژگی‌های تصمیمی

ویژگی‌های تصمیمی سؤالهایی است که دربارهٔ یک اتوماتا یا یک زبان می‌توانیم بپرسیم. در زیر نمونه‌ای از آنها را مشاهده می‌کنید.

• مسئله عضویت

آیا رشتهٔ w متعلق به زبان L است؟

• مسئله تهی بودن

آیا زبان L تهی است؟ برای پاسخ به این سؤال باید به این سؤال جواب داد که آیا مسیری در اتوماتای A که زبان L را می‌پذیرد وجود دارد که ما را از یک حالت آغازین به یک حالت پایانی برساند؟

• مسئله متناهی بودن

آیا در زبان L تعداد محدودی رشته وجود دارد؟ برای پاسخ به سؤال ذکر شده دو راهکار یا لم وجود دارد. لم1: اگر DFA دارای n حالت باشد و رشته‌ای با طول n یا بیشتر را بپذیرد، آنگاه زبان DFA نامتناهی است. لم2: اگر رشته‌ای با طول n یا بیشتر در زبان L (که DFAی معادلی با n حالت دارد) وجود داشته باشد، آنگاه رشته‌ای با طول بین n و 2n-1 نیز دارد.

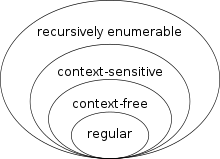
زیرمجموعه‌ها

• زبان‌های متناهی، که مجموعه‌هایی شامل تعداد متناهی رشته هستند.
• زبان‌های بی‌ستاره، شامل رشته‌هایی که توسط عبارت‌های منظم، از رشته‌های تهی، نمادهای الفبا و اعمال جبری و الحاق روی آن‌ها به دست می‌آیند. از ستاره کلین نمی‌توان در آن‌ها استفاده کرد. این دسته از زبان‌ها، شامل همهٔ زبان‌های متناهی‌اند.

منابع

An Introduction to Formal Languages and Automata، Peter Linz

Introduction to the Theory of Computation، Michael Sipser