سری لوران
در ریاضیات، سری لوران یک تابع مختلط f(z) یک نمایش از آن تابع به صورت سری توانی است که شامل جملاتی از درجه منفی است. این سری میتواند برای نمایش توابع مختلط در حالتی که یک بسط سری تیلور نمیتواند به کار رود استفاده شود. سری لوران پس از اینکه توسط پیر آلفونس لوران در ۱۸۴۳ انتشار یافت، نامگذاری شد. ابتدا کارل وایرشتراس آن را در ۱۸۴۱ کشف کرد ولی منتشر نکرد. سری لوران برای تابع مختلط f(z) حول نقطه c بهوسیلهی:
که an ثابتهایی هستند که با یک انتگرال خطی که یک کلیت از فرمول انتگرال کوشی است تعریف میشوند:
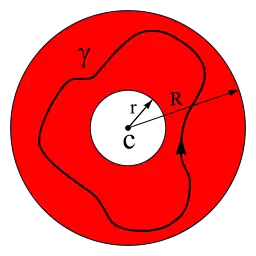
مسیر انتگرالگیری γ پادساعتگرد حول یک منحنی تصحیحپذیر بسته است که هیچ همپوشانی ندارد و c را در بر گرفتهاست و درون طوقهٔ A است که در آن f(z) هولومورفیک است. بسط f(z) در هر جای این طوقه معتبر خواهد بود. در عمل، این فرمول به ندرت استفاده میشود زیرا محاسبهٔ انتگرالها مشکل است. به جای آن، سری لوران بهوسیله آمیختن با بسط تیلور قطعه به قطعه سر هم میشود. اعداد an و c معمولاً عدد مختلط گرفته میشوند، اگرچه احتمالات دیگری نیز وجود دارد.
سری لوران همگرا
سری لوران با ضرایب مختلط ابزار مهمی در آنالیز مختلط است، مخصوصا برای تجسس رفتار تابع در نزدیکی نقاط تکین. برای نمونه تابع f(x) = e−1/x² با f(0) = 0 را در نظر بگیرید. به عنوان یک تابع حقیقی، همه جا بینهایت بار مشتقپذیر است. با این وجود به عنوان یک تابع مختلط در x = 0 با جایگزینی x با −1/x2 در سری توانی تابع نمایی سری لوران آن را میسازیم که همگراست و برابر f(x) است برای تمام اعداد مختلط x به جز در نقطه تکین x=0. بهطور کلی تر سری لوران میتواند برای نمایش توابع هولومورفیک تعریف شده روی یک طوقه به کار رود، اگر چه سری توانی برای نمایش توابع هولومورفیک تعریف شده روی یک دیسک استفاده شود. فرض کنید
یک سری لوران با ضرایب مختلط an و مرکز مختلط c است. آنگاه یک شعاع داخلی منحصربفرد r و یک شعاع خارجی منحصربفرد R وجود دارد که:
- سری لوران روی طوقهٔ باز A := {z : r < |z − c| < R} همگراست. وقتی میگوییم سری لوران همگراست، یعنی هردو سری توانی با درجه مثبت و سری توانی با درجه منفی همگرایند. بعلاوه، این همگرایی روی مجموعههای فشرده یکشکل خواهد بود. نهایتا سری همگرا یک تابع هولومورفیک روی طوقهٔ باز تعریف میکند.
- خارج از طوقه، سری لوران واگراست. یعنی برای هر نقطه خارج A سری با درجه مثبت یا سری با درجه منفی واگراست.
- راجع به مرز طوقه، نمیتوان اظهار نظر کرد.
ممکن است r صفر باشد یا R بینهایت باشد. لزوما هم این صحیح نیست که r کوچکتر از R است. این شعاعها به صورت زیر میتوانند محاسبه شوند:
R را بینهایت میگیریم وقتی که lim sup صفر باشد. برعکس اگر با یک طوقه به شکل A = {z : r < |z − c| < R} و تابع هولومورفیک f(z) تعریف شده بر A شروع کنیم، آنگاه همیشه یک سری لوران منحصربفرد با مرکز c وجود دارد که (حداقل) روی A همگراست و نمایانگر تابع f(z) است.
منبع
Wikipedia contributors, "Laurent series," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Laurent_series&oldid=187741784 (accessed February 22, 2008).