شار
شار یا شاریدگی در شاخههای مختلف علم فیزیک به صورت زیر تعریف شدهاست:
- در پدیدههای انتقال (انتقال حرارت، انتقال جرم و دینامیک سیالات) شار در اصل به معنای جا به جایی یک حجم از کمیتی جابهجا شونده از یک سطح خاص است است. در واقع، شار عبورکننده از یک سطح دلخواه، مقدار حجمی است از یک کمیت (مانند آب، شار الکتریکی، جریان الکتریکی و …) که در واحد زمان، در جهت عمود برسطح (یا مؤلفهٔ عمودی بردارِ سطح) از سطح مورد نظر عبور میکند.
- برای آشنایی بیشتر با مفهوم شار، میتوان مثالهای زیر را با دقت بررسی کرد:
- مطابق شکل، سه حجم از آب را در نظر بگیرید که در یک ثانیه ازسمت چپِ سطح مشخص شده در شکل با مساحت s به سمت راست آن منتقل میشود:
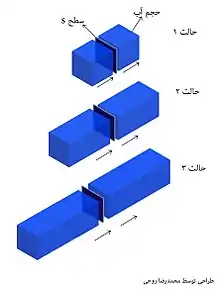 این تصویر سه حالت از عبور حجمی از آب از سمت چپ سطح s به سمت راست آن را نشان میدهد. تمام این حجمها در واحد زمان (برای مثال یک ثانیه) از سطح s عبور میکنند. درحالت سوم، حجم آب عبوری از سطح s در یک ثانیه، بیشتر است. پس سرعت عبور آب در حالت سوم بیشتر است؛ بنابراین، شار عبوری از سطح s در حالت سوم بیشتر است .
این تصویر سه حالت از عبور حجمی از آب از سمت چپ سطح s به سمت راست آن را نشان میدهد. تمام این حجمها در واحد زمان (برای مثال یک ثانیه) از سطح s عبور میکنند. درحالت سوم، حجم آب عبوری از سطح s در یک ثانیه، بیشتر است. پس سرعت عبور آب در حالت سوم بیشتر است؛ بنابراین، شار عبوری از سطح s در حالت سوم بیشتر است . - تمامی این حجمها در واحد زمان (برای مثال یک ثانیه) از سطح s عبور میکنند. همانطوریکه مشاهده میشود، درحالتِ سوم، حجم آب عبوری از سطح s در یک ثانیه، بیشتر است. پس سرعت عبور آب در حالت سوم بیشتر است؛ بنابراین، شار عبوری از سطح s در حالت سوم بیشتر است.
- اگر بخواهیم تعریف شار را به صورت یک فرمول دربیاوریم، یک حجم را در نظر میگیریم که حاصل ضرب یک سطح (همان سطح s) و یک ارتفاع است. سطح s، همان سطحی است که حجم کمیت مورد نظر ما از آن عبور میکند و اتفاع ذکر شده، در ریاضیات، به چگالی سطحی شار معروف است. پس خواهیم داشت:
- {{{1}}}
- که در فرمول بالا:
- V=شار عبوری از سطح S
- S= سطحی که شار آز آن میگذرد
- D= چگالی شار (ارتفاع مورد نظر)
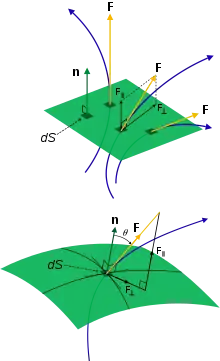
- اما فرمول بالا فرمول کاملی نیست. در تعریف شار بیان شد که حجم کمیت عبوری (مثلاً آب) باید به صورت عمود برسطح از آن عبور کند و در غیر این صورت، هنگام عبور حجم مورد نظر از سطح، باید مولفهٔ عمودی بردار سطح در ارتفاع یا چگالی شار ضرب شود. به همین دلیل، چگالی شار و سطح به صورت دو بردار در نظر گرفته میشوند که با ضرب داخلی در هم ضرب میشوند؛ لذا تعریف نهایی شار عبوری از سطح به صورت زیر تکمیل میشود:
- شار: {{{1}}}
- که در آن S و D به ترتیب بردار سطح و بردار چگالی سطحی شار هستند که به صورت پر رنگ شده به نشانه بردار بودن نمایش داده شدهاند.
- نکته: منظور از بردار سطح، برداری است که مانند همهٔ بردارها دارای اندازه و جهت است که اندازه آن برابر مساحت سطح و جهت آن، جهت عمود بر سطح است.
- شار همانطوریکه بیان شد، یک حجم است که حاصل ضرب دو بردار میباشد و یک کمیت اسکالر است. از آن جایی که یک سطح ممکن است به صورت منحنی باشد و همچنین بردار چگالی شار ممکن است در تمام نقاط سطح مقدار ثابتی نداشته باشد و وابسته به دستگاه مختصات به صورت یک تابع تغییر کند، بهتر است سطحِ خود را در این حالت به تعداد زیادی قطعات بسیار کوچک تقسیم کنیم تا بتوانیم با تقریبی خوب، بردار چگالی شار را در هر قطعه ثابت فرض کنیم، سپس حاصل ضرب بردار چگالی شار در تمام قطعات را باهم جمع کنیم. هر قدر این قطعات کوچکتر باشند، میزان دقت نتیجه بدست آمده بیشتر است. اگر این قطعات بینهایت کوچک شوند، به مفهوم انتگرال میرسیم که تعریف شار را به صورت زیر بهبود میبخشد:
- شار: {{{1}}}
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.