شبکه شاره
برای تحلیل شبکههای حمل و نقل که وسیله حمل کالاها از مراکز تولید به بازار هستند یا شبکههای مخابراتی که دادهها را منتقل میکنند یا شبکههای رایانهای یا شبکه خطوط انتقال گاز در شهرها را توسط گرافهای سودار مورد تحلیل قرار میدهیم. مشاهده میشود که در اینگونه شبکهها، گراف معادل نیازمند ساختار یا مؤلفههایی اضافی است. مثلاً بهطور خاص بایستی هر یال سودار دارای عدد مثبت یا صفری به عنوان میزان ظرفیت آن باشد که این عدد نشان دهنده ظرفیت حمل داده در این خط است.تحلیل شبکههای شاره دارای دامنه وسیعی از این کاربردهاست.
پیشینه تاریخی
در ۱۹۳۰ بیان مسئله راهآهن شوروی موجب تحریک آمریکاییها برای حل این مسئله شد. در ابتدای سال ۱۹۵۵این مسئله توسط تی. ای. هریس[1] به صورت دیگری بیان شد: شبکهٔ راهآهنی را در نظر بگیرید که دو شهر را از طریق تعدادی شهرهای میانی به هم وصل کردهاست. در این شبکه، هر مسیر دارای عددی است که نشان دهنده ظرفیت انتقال آن مسیر میباشد. وضعیت پایداری را در نظر بگیرید؛ بیشترین شارهای که میتواند از هر شهر دلخواه خارج شود و به شهر مشخص دیگری وارد شود، چقدر است؟ فورد و فالکرسون بیان کردند که هریس در سال ۹۵ یک مدل ساده از جریان ترافیک در این مسئله ارائه کرد.
تعریف
گراف سودار (G=(V،E را یک شبکه شاره مینامیم اگر:
- اولاً هر یال v،u)€ E) دارای یک میزان ظرفیت غیر منفی یعنیc(u،v)≥۰ است. برای زوجهای (u،v) که در E وجود ندارند ظرفیت آنها را صفر فرض میکنیم. همچنین چنانچه E دارای یالی مانند (u,v) باشد، یال (v,u) در جهت مخالف آن در گراف موجود نباشد.
- ثانیاً دو راس مجزای s با نام منبع و t با نام چاهک در این گراف وجود دارد که s فقط مبدأ چند یال و t فقط مقصد چند یال است و هر راس دیگر گراف در مسیری از s به t قرار میگیرد.
شرط شارش
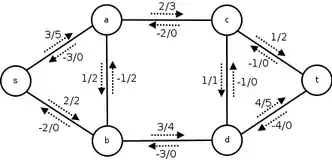
اگر (G=(V،E یک شبکه شاره با منبع s و چاهک t باشد، یک شارش در G f:V×V تابع است که سه شرط زیر را ارضا میکند:
- ۱»شرط محدودیت ظرفیت: برای هر u،v€ V بایستی (f(u،v)≤c(u،v باشد.
- ۲»شرط تقارن شارش: برای هر u،v€ V بایستی (f(u،v)= - f(v،u باشد.
- ۳»شرط بقای شارش: برای هر {u€V – {s،t بایستی v∈V) f(u،v) =۰)_∑ باشد.
اندازه شارش
مقدار شارش در هر یال میتواند عدد حقیقی منفی یا مثبت یا صفر باشد. اندازه شارش f را مساوی مقدار شارش خروجی از منبع تعریف میکنیم. یعنی: (f| = ∑_(v∈V)f(s،v|
کاربرد
یک مسئله مهم در مورد شبکههای شاره، یافتن [شارش بیشینه] است.از دیدگاه کاربردی تابع شارش بیشینه نشان دهنده بهترین روش استفاده از شبکه شاره در انتقال کالا یا داده از منبع به چاهک است. الگوریتم فورد-فالکرسون شارش بیشینه در یک شبکه شاره را به دست میدهد.
منابع برای مطالعه بیشتر
- مقدمهای بر الگوریتمها - پدیدآورنده: تامس کورمن، چارلز لیزرسان، رونالد دیوست، کلیفورد اشتاین - گروه مهندسی-پژوهشی خوارزمی (مترجم) - ناشر: درخشش
- ریاضیات گسسته و الگوریتم ها-پدیدآورنده:علی بهفروز، محمد ایزدی-ناشر:آییژ
- T.E. Harris