ضرب با انگشتان

روشی که با استفاده از انگشتان دو دست می‌توان حاصل ضرب اعداد بزرگتر از ۵ را به دست آورد.[1][2]

تاریخچه

اکثر باستانیان روش‌هایی را برای نمایش اعداد طبیعی به وسیله وضعیت‌های مختلف انگشتان ابداع کرده بودند. یونانی‌ها، رومی‌ها، مسلمانها، هندیها و بسیاری اقوام دیگر چنین روش‌هایی داشته‌اند. در اروپای قرون وسطی، نمایش اعداد به کمک انگشتان به عنوان زبان بین‌المللی برای ارتباط بین اقوام مختلف بسیار متداول بوده‌است. این زبان هنگام معامله در بازارهای بین‌المللی و موقعیت‌های دیگری که زبان مانعی بر سر راه ارتباط بود به کار می‌رفت. امروزه نیز اعداد انگشتی در مشرق زمین به همین منظور به کار می‌روند. از نمایش انگشتی اعداد، شکل‌هایی از محاسبه با انگشت به وجود آمد. این روش‌های محاسبه از شمارش ساده تا حالت‌های خاصی از ضرب را در برمی گیرند. برخی از این روش‌ها در قرون وسطی کاربرد عام داشته‌اند و یکی از این گونه روش‌ها تا اوایل قرن بیستم هم در برخی از نقاط روستایی روسیه و فرانسه به کار می‌رفت. این روش را گاهی ضرب روستایی اروپایی می‌نامند.[3]

روش ضرب با انگشتان برای اعداد ۵ تا ۱۰

ضرب 8 در 9 با انگشتان

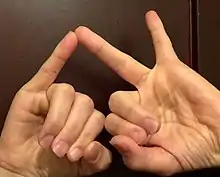
مثال: فرض کنید بخواهیم حاصل ضرب ۸×۹ را به دست آوریم. ابتدا هر یک از این اعداد را به صورت جمعی از عدد ۵ می‌نویسیم.

۸=۵+۳ و ۹=۵+۴ بنابراین

8×9=(5+3)(5+4)

به همین دلیل ۴ انگشت یک دست و ۳ انگشت دست دیگر را می‌خوابانیم. انگشتهای خوابانده شده نشان دهنده تعداد دهگان حاصل ضرب می‌باشند که در این مثال برابر با ۷=۳+۴ می‌باشد؛ و رقم یکان این حاصل ضرب برابر با ۱×۲=۲ می‌باشد که ۲ انگشتهای باز یک دست و ۱ انگشت باز دست دیگر است.[4]

روش ضرب با انگشتان برای اعداد ۱۱ تا ۱۵

ضرب ۱۳ در ۱۴با انگشتان

مثال: فرض کنید بخواهیم حاصل ضرب ۱۴×۱۳ را به دست آوریم. دو دست خود را طوری نگه می‌داریم که پشت آنها به روی خودمان باشد. در هر دست از انگشت شصت تا انگشت کوچک را به ترتیب از ۱۱ تا ۱۵ شماره گذاری می‌کنیم. دو انگشتی که عدد ۱۳ و عدد ۱۴ را در هر دو دست نشان می‌دهند، روی هم قرار می‌دهیم؛ و انگشتان بعد از این دو عدد را می‌خوابانیم. حاصل ضرب ۱۴×۱۳ برابر است با مجموع حاصل ضرب تعداد انگشتانی که باز هستند در ۱۰ به اضافه مجموع انگشتان باز، به اضافه 100:[4]

${\displaystyle 13\times 14=7\times 10+3\times 4+100=182}$

اثبات درستی این رابطه

اگر بخواهیم حاصل ضرب دو عدد ${\displaystyle x}$ و ${\displaystyle y}$ را به دست آوریم، به طوریکه ${\displaystyle 11\leq x\leq 15}$و ${\displaystyle 11\leq y\leq 15}$باشند. ${\displaystyle x-10}$و ${\displaystyle y-10}$تعداد انگشتان باز در هر دست می‌باشند؛ بنابراین حاصل ضرب ${\displaystyle x\times y}$برابر است با:

${\displaystyle x\times y=10[(x-10)+(y-10)]+(x-10)(y-10)+100=10[x+y-20]+(x-10)(y-10)+10=10x+10y-200+xy-10x-10y+100+100=xy}$

روش ضرب با انگشتان برای اعداد ۱۶ تا ۲۰

ضرب 16 در 19 با انگشتان

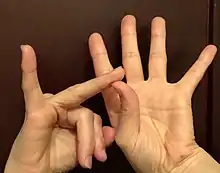
مثال: فرض کنید بخواهیم حاصل ضرب ۱۹×۱۶ را به دست آوریم. در هر دست از انگشت شصت تا انگشت کوچک را به ترتیب از ۱۶ تا ۲۰ شماره گذاری می‌کنیم. دو انگشتی که عدد ۱۶ و عدد ۱۹ را در هر دو دست نشان می‌دهند، روی هم قرار می‌دهیم؛ و انگشتان بعدی را می‌خوابانیم. حاصل ضرب ۱۹×۱۶برابر است با مجموع حاصل ضرب مجموع انگشتان باز در ۲۰ به اضافه حاصل ضرب انگشتان باز در هر دو دست به اضافه 200:[4]

${\displaystyle 16\times 19=5\times 20+4\times 1+200=304}$

اثبات درستی این رابطه

اگر بخواهیم حاصل ضرب دو عدد ${\displaystyle x}$ و ${\displaystyle y}$ را به دست آوریم، به طوریکه ${\displaystyle 16\leq x\leq 19}$و ${\displaystyle 16\leq y\leq 19}$باشند. ${\displaystyle x-15}$ و ${\displaystyle y-15}$ تعداد انگشتان باز در هر دست می‌باشند؛ بنابراین حاصل ضرب ${\displaystyle x\times y}$برابر است با:

${\displaystyle x\times y=20[(x-15)+(y-15)]+(20-x)(20-y)+200=20[x+y-30]+(20-x)(20-y)+200=20x+20y-600+400-20y-20x+xy+200=xy}$

تعمیم این روش برای اعداد بزرگتر

این روش ضرب را می‌توان برای اعداد بزرگتر نیز استفاده نمود، با این شرط که هر دو عدد در یک دسته ۵ تایی مثل ۲۱ تا ۲۵، ۲۶ تا ۳۰ و دسته‌های مشابه بزرگتر قرار گرفته باشند.[4]

منابع

1. شهریاری، پرویز (۱۳۹۳). در پی فیثاغورث. انتشارات امیرکبیر. صص. ۱۲۴.
2. توکلی صابری، علیرضا (۱۳۸۱). تفریح با ریاضی. انتشارات مدرسه. صص. ۱۳۸.
3. دیویس، هارولد (۱۳۸۴). تاریخ محاسبه. شرکت انتشارات علمی و فرهنگی. صص. ۶۹.
4. «let your fingers do the multiplying» (PDF). بایگانی‌شده از اصلی (PDF) در ۱۹ مارس ۲۰۱۳. دریافت‌شده در ۱۱ فوریه ۲۰۱۹.