عرض درخت

در نظریه گراف، عرض درختی یک گراف بدون جهت، عددی‌ است که مربوط به آن گراف است. این عدد می‌تواند به طرق مختلفی تعریف شود: اندازهٔ بزرگ‌ترین راس در تجریهٔ درختی آن گراف، اندازهٔ بزرگ‌ترین خوشه در تکمیل وتری و ... . مفهوم عرض درختی یک گراف، در ابتدا توسط Umberto Bertelé و Francesco Brioschi در سال ۱۹۷۲ معرفی شد. بعدها به‌صورت جدی توسط Neil Robertson و Paul Seymour در سال ۱۹۸۴ مجدداً معرفی گردید. برای تعریف عرض درختی یک گراف، ابتدا باید تجریهٔ درختی گراف را تعریف کنیم.

تجزیه‌ی درختی

تجزیهٔ درختی گراف ${\displaystyle G=(V,E)}$، درختی‌ است مانند ${\displaystyle T}$ با رئوس ${\displaystyle X_{1},X_{2},...,X_{n}}$ (به این رئوس کیف یا bag می‌گویند) که در آن هر ${\displaystyle X_{i}}$ یک زیرمجموعه‌ای از ${\displaystyle V}$ است که شرایط زیر را ارضا کند:

1. اجتماع تمامی ${\displaystyle X_{i}}$ها، مجموعهٔ ${\displaystyle V}$ باشد.
2. تمامی رئوس (کیف‌های) درخت که شامل راس ${\displaystyle v\in V}$ هستند، تشکیل یک زیردرخت هم‌بند بدهند.
3. برای هر یال مانند ${\displaystyle (u,v)}$ در گراف ${\displaystyle G}$، حداقل یک راس (کیف) مانند ${\displaystyle X_{i}}$ در درخت باشد که شامل هر دو راس ${\displaystyle u}$ و ${\displaystyle v}$ است.

تجزیهٔ درختی یک گراف، یکتا نیست. بدیهی‌ترین تجزیهٔ درختی، قراردادن تمامی رئوس گراف در یک کیف است که در این صورت هر گراف یک تجزیه با عرض ${\displaystyle n-1}$ دارد؛ بنابراین برای هر گراف تجزیه‌های درختی متعددی وجود دارد. عرض درختی یک تجزیهٔ درختی، برابر است با سایز بزرگ‌ترین کیف آن منهای یک. عرض درختی یک گراف نیز که با ${\displaystyle tw(G)}$ نمایش داده می‌شود، برابرست با کم‌ترین عرض درختی میان تمامی تجریه‌های درختی آن گراف.

مثال: در شکل زیر گراف ${\displaystyle G}$ و یک تجزیهٔ درختی از آن را می‌بینید. عرض این تجزیهٔ درختی، ۲ می‌باشد.

یک گراف به همراه یک تجزیهٔ درختی از آن با عرض ۲

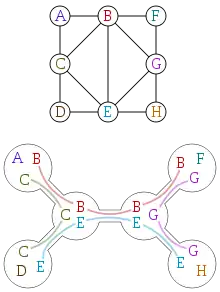
مثال: عرض درختی تمام درخت‌ها برابر با یک است.

تجزیه‌ی درختی نرم

تجزیهٔ درختی ${\displaystyle ({X_{i}|i\in I},T(I,F))}$ با عرض k نرم می‌گوییم اگر:

• ${\displaystyle \forall i\quad |X_{i}|=k+1}$
• ${\displaystyle \forall {i,j}\in F\quad |X_{i}\bigcap X_{j}|=k}$

نکته: هر تجزیهٔ درختی را می‌توان به یک تجزیهٔ درختی نرم تبدیل کرد.

مجموعه‌ی مستقل بر روی تجزیه‌ی درختی

فرض کنید ${\displaystyle ({X_{i}|i\in I},T(I,F))}$ یک تجزیهٔ درختی برای گراف ${\displaystyle G=(V,E)}$ باشد به طوری که عرض آن حداکثر ${\displaystyle k}$ باشد. می‌خواهیم الگوریتمی از ${\displaystyle O(k^{2}4^{k}|V|)}$ ارائه دهیم تا بزرگ‌ترین مجموعهٔ مستقل این گراف را پیدا کنیم.

ابتدا درخت را از راس دلخواه r ریشه دار می‌کنیم. به ازای هر ${\displaystyle U\subseteq X_{i}}$، ${\displaystyle dp(i,U)}$ را برابر با بزرگ‌ترین مجموعهٔ مستقل که می‌توان در زیر درخت i پیدا کرد به شرط آن که اشتراک راس‌های مجموعهٔ مستقل و ${\displaystyle X_{i}}$ دقیقا راس‌های U باشد تعریف می کنیم. حال الگوریتم جستجوی عمق اول را روی درخت اجرا می ‌کنیم. سپس به ازای هر راس i یکی از کارهای زیر را انجام می دهیم:

• اگر راس ${\displaystyle i}$یک برگ بود، به ازای هر ${\displaystyle U\subseteq X_{i}}$ اگر U یک مجموعهٔ مستقل در گراف بود ${\displaystyle dp(i,U)=\left\vert U\right\vert }$ در نظر می گیریم در غیر این صورت ${\displaystyle dp(i,U)=-\infty }$
• اگر راس ${\displaystyle i}$برگ نبود و ${\displaystyle c_{1},c_{2},\dots ,c_{l}}$فرزندان راس ${\displaystyle i}$باشند آنگاه:

${\displaystyle dp(i,U)=|U|+\sum _{j=1}^{l}max(dp(j,W)|W\subseteq (X_{c_{j}}-U)\quad and\ W\cup U\ is\ independent)}$

جواب نیز برابر خواهد شد با:

${\displaystyle max(dp(r,U)|U\subseteq X_{r}}$ تعداد حالاتی که مقادیر آن‌ها را پیدا می‌کنیم برابر با ${\displaystyle 2^{k}|V|}$ است. هم‌چنین برای به دست آوردن مقدار یک خانه باید به ازای تمام زیرمجموعه از بسته‌های فرزندانش مقدار ماکسیمم حساب شود و همچنین باید بررسی شود که راس‌ها به هم یال نداشته باشند که مرتبهٔ این قسمت نیز از ${\displaystyle O(2^{k}k^{2})}$ است. در نتیجه زمان اجرای الگوریتم ${\displaystyle O(k^{2}4^{k}|V|)}$ خواهد شد.

به ازای k‌های کوچک اثبات شده‌است که گرافی که مجموعهٔ گراف‌های زیر را به عنوان ماینور شامل نمی شود ، عرض درختی کمتر مساوی k دارد.

• ${\displaystyle k=0\rightarrow k_{2}}$
• ${\displaystyle k=1\rightarrow k_{3}}$
• ${\displaystyle k=2\rightarrow k_{4}}$
• ${\displaystyle k=3\rightarrow k_{5},k_{2,2,2}}$
• ${\displaystyle k=4\rightarrow }$ بیش از ۷۵ نوع گراف [1]

الگوریتم‌های محاسبهٔ عرض درختی یک گراف

در حالت کلی، پاسخ به این سؤال که آیا گراف ${\displaystyle G}$ عرض درختی‌اش حداکثر ${\displaystyle k}$ است یا نه یک مسئله ${\displaystyle NP-complete}$ (ان‌پی کامل) است. اما برای ${\displaystyle k}$های مشخص با اندازهٔ کوچک الگوریتمی با زمان اجرای خطی وجود دارد. زمان اجرای این الگوریتم بر اساس سایز ورودی خطی ولی بر اساس ${\displaystyle k}$ نمایی‌ست و لذا فقط برای ${\displaystyle k}$های ثابت و کوچک عملی‌ است.[2]

مسئله‌ی دزد و پلیس‌ها

در این مثال در یک گراف تعدادی پلیس حضور دارند که در راس‌های مختلف گراف قرار دارند. یک دزد نیز در یکی از راس‌های گراف پنهان شده‌است. در هر مرحله اگر k پلیس داشته باشیم ، پلیس‌ها k راس را در نظر می‌گیرند و به آن می‌روند. سپس دزد یک راس را در نظر می‌گیرد که در آن پلیس نیست و از راسی که در آن حضور دارد به راس مقصد مسیری وجود داشته باشد که راس‌های این مسیر شامل راس‌های اشتراک مکان‌های قبلی پلیس‌ها و مکان‌های جدید پلیس‌ها نباشد. پلیس‌ها برنده می‌شوند اگر بعد از تعداد محدودی مرحله ، دزد راسی برای فرار کردن به آن نداشته باشد.

قضیه : اگر عرض درختی گراف G حداکثر k باشد ، آنگاه 1 + k پلیس می توانند دزد را دستگیر کنند.

اثبات: چون عرض درختی گراف حداکثر k است ، یک تجزیهٔ نرم برای آن وجود دارد. حال تجزیهٔ نرم آن را در نظر می گیریم. ابتدا آن را از راسی ریش‌دار می کنیم. پلیس‌ها در مرحله اول در 1 + k راس در بستهٔ ریشه قرار می‌گیرند. دزد نیز در این مرحله در راسی دیگر قرار گرفته‌است. حال راسی که دزد در آن قرار گرفته را در نظر می‌گیریم. مجموعهٔ بسته‌هایی که راس دزد در آن قرار دارد یک مجموعهٔ همبند در یکی از زیر درخت‌های فرزندان ریشه است. پلیس‌ها در این مرحله آن فرزند را انتخاب می‌کنند و به راس‌های آن منتقل می‌شوند و از آن جا که اشتراک بستهٔ جدید با بستهٔ قبل k است و یک برش در گراف را تشکیل می‌دهد ، دزد نمی‌تواند از آن خارج شود. اگر پلیس‌ها به همین روند ادامه دهند در آخر دزد را در یک بسته برگ گیر می‌اندازند. [3]

منابع

1. https://www.ti.inf.ethz.ch/ew/lehre/GA07/lec-treewidth.pdf
2. Bodlaender, Hans L. (1996), "A linear time algorithm for finding tree-decompositions of small treewidth", SIAM Journal on Computing, 25 (6): 1305–1317
3. «نسخه آرشیو شده» (PDF). بایگانی‌شده از اصلی (PDF) در ۲۷ سپتامبر ۲۰۱۶. دریافت‌شده در ۲۰ مه ۲۰۱۷.