قانون براگ

در فیزیک قانون براگ نتایج آزمایش‌هایی است که در آن پرتو ایکس یا نوترون به سطح بلورین تابیده می‌شد که برای اولین بار توسط فیزیکدان ویلیام لارنس براگ بررسی شد[1] که آزمایش‌هایش در سال ۱۹۱۱ و در دانشگاه کمبریج انجام شد. به‌طور ساده هنگام تابانیدن پرتوهایی مانند پرتو ایکس یا نوترون به سطوح بلورین بازتابش‌هایی انجام می‌گیرد که به این بازتاب‌ها پراش یا فرانژ گویند، که به همین دلیل براگ جایزه نوبل فیزیک را در سال ۱۹۱۵ به دست آورد سطوح بلورینی که او بررسی کرده بود عبارتنداز NaCl، ZnS، و الماس.

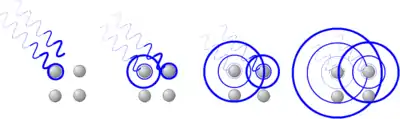
قانون براگ براین اساس است که پرتوهای با طول موج مشخص و با زاویه مشخص به جسم بلورین تابانده می‌شود و با برخورد به اتم‌های مختلف جسم با تاخیر فازهای مختلف باز تابش‌هایی ایجاد می‌شود . این پرتوهای باز تابش شده در زاویه تتا با توجه به تاخیر فازهای مختلفشان حداکثر مقدار برهمکنشی را خواهند داشت. زاویه تتا وابسته به فاصله صفحه‌های کریستالی ویا فاصله اتمی آن‌ها می‌باشد با این روش میتوان با توجه به زاویه حداکثر بازتابش پرتو انعکاس یافته از شبکه بلورین فاصله اتم جسم ویا فاصله صفحات کریستالی را بدست آورد.از طرفی می‌توان با مشخص بودن فاصله صفحات کریستالی جسم ، زاویه تابش و زاویه حداکثر باز تابش طول موج تابش الکترومغناطیسی را بدست آورد.که از فرمول زیر تبعیت می‌کند

[2][3]

${\displaystyle n\lambda =2d\cdot \sin \theta \,}$

که

• n مرتبه بازتاب است و می‌تواند اعداد صحیح کوچکی باشد(تعداد صفحه‌های کریستالی )،
• λ طول موج پرتو ایکس است که الکترون یا نوترون را جابجا نموده است،
• d فضای خالی میان اتمهاست و
• θ زاویه‌ای که پرتوهای بازتابیده شده بیشترین دامنه را دارند با راستای تابش پرتو‌های اولیه .

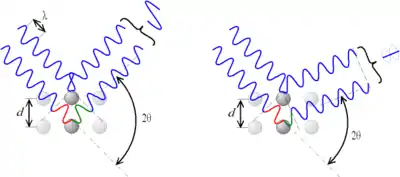
According to the ۲θ deviation، the phase shift causes constructive (left figure) or destructive (right figure) interferences

حرکت پروتون‌ها و نوترون‌ها و الکترون‌ها وابسته است به طول موج دوبروی آن‌ها .

روش بدست آوردن فضای میان اتمها

برای بدست آوردن فضای میان اتمها می‌توان از حجم اتم‌ها چشم پوشید و آن را به صورت زیر نوشت:

${\displaystyle {\frac {1}{d^{3}}}={\frac {n}{v}}}$

که در آن d فاصلهٔ میان اتم‌هاست nتعداد اتم‌ها و vحجم جامد بلورین است تعداد اتم‌ها را می‌توان به راحتی از فرمول زیر بدست آورد:

${\displaystyle n=N_{A}.Norn=N_{A}.{\frac {m}{M}}}$

که در آن ${\displaystyle N_{A}}$ عدد آووگادرو٬ N تعداد مول اتم‌هاm٬جرم ماده وM جرم مولی است.[4]

اثبات

یک پرتو تکرنگ هنگامی که به سطح بلورین منظمی که فاصله اتمهایش d هستند می‌تابد بعضی از پرتوها با زاویه تتا بازمی گردند به صورتی که:

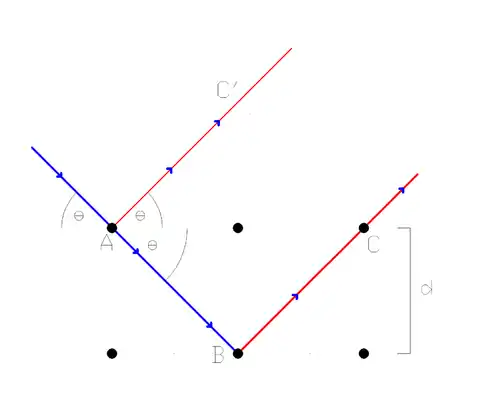
برای اینکه بازتابش صورت گیرید باید فاصله‌ی${\displaystyle (AB+BC)-(AC')\,}$مضربی از طول موج باشد بنابرین:

${\displaystyle (AB+BC)-(AC')=n\lambda \,}$

که در آن مضرب با n و λ طول موج است

با استفاده از Pythagorean theorem نشان می دهیم:

${\displaystyle AB={\frac {d}{\sin \theta }}\,}$ and ${\displaystyle BC={\frac {d}{\sin \theta }},}$ and ${\displaystyle AC={\frac {2d}{\tan \theta }}\,}$

بنابراین تبدیل می‌شود:

${\displaystyle AC'=AC\cdot \cos \theta ={\frac {2d}{\tan \theta }}\cos \theta \,}$

تابعهای سینوسی را جایگزین می کنیم:

${\displaystyle n\lambda ={\frac {2d}{\sin \theta }}-{\frac {2d}{\tan \theta }}\cos \theta ={\frac {2d}{\sin \theta }}(1-\cos ^{2}\theta )={\frac {2d}{\sin \theta }}\sin ^{2}\theta }$

ساده می کنیم:

${\displaystyle n\lambda =2d\cdot \sin \theta \,}$

و این قانون براگ است.

منابع

W.L. Bragg، "The Diffraction of Short Electromagnetic Waves by a Crystal"، Proceedings of the Cambridge Philosophical Society، ۱۷ (۱۹۱۴)، ۴۳–۵۷.

1. There are some sources, like the Academic American Encyclopedia, that attribute the discovery of the law to both W.L Bragg and his father W.H. Bragg, but the official Nobel Prize site and the biographies written about him (Light Is a Messenger: The Life and Science of William Lawrence Bragg, Graeme K. Hunter, 2004 and “Great Solid State Physicists of the 20th Century", Julio Antonio Gonzalo, Carmen Aragó López) make a clear statement that William Lawrence Bragg alone derived the law.
2. See for example this example calculation بایگانی‌شده در ۱۰ ژوئیه ۲۰۱۱ توسط Wayback Machine of interatomic spacing with Bragg's law.
3. کتاب مبانی فیزیک نوین نوشته رایچارد وایدنر و رابرت سلز صفحات ۲۰۸ تا۲۱۰
4. کتاب مبانی فیزیک نوین نوشته رایچارد وایدنر و رابرت سلز صفحه ۲۰۹

• مشارکت‌کنندگان ویکی‌پدیا. «Bragg's law». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۵ ژوئن ۲۰۰۸.

جستارهای وابسته

• ساختار بلورین
• طول موج
• پرتو ایکس
• پراش براگ