قضیه دزارگ
در هندسه تصویری، قضیه دزارگ که به افتخار جرارد دزارگ نامگذاری شده است بیان می دارد که:
دو مثلث تجانس محوری دارند اگر و تنها اگر تجانس مرکزی داشته باشند.
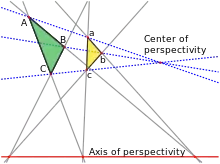
مثلثهای همرس (مثلث هایی با خاصیت مناظر و مرایا). زمانی که اضلاع متناظر در دو مثلث توسعه پیدا می کنند، در نقطه ای روی خطی به نام محور تجانس به هم می رسند. خطوطی که از رأس های متناظر روی مثلث ها عبور می کنند ممکن است در نقطه ای به نام مرکز تجانس به هم برخورد کنند. قضیه دزارگ بیان می دارد که اولین شرط (بر خورد امتداد اضلاع بر روی محور تجانس) شرط لازم و کافی برای رسیدن به خاصیت دوم (همرسی خطوط عبوری از رأس ها در مرکز تجانس) می باشد.
سه رأس یکی از مثلث ها را با ، و و رئوس مثلث دیگر را با ، و نامگذاری می کنیم. تجانس محوری به معنای این است که خطوط و در یک نقطه، خطوط و در نقطه دوم و خطوط و در نقطه سوم همرسند. و هر سه این نقاط بر روی خط مشترکی به نام محور تجانس قرار دارند. تجانس مرکزی بدین معناست که سه خط ، و در یک نقطه به نام مرکز تجانس همرسند.
یادداشتها
- مشارکتکنندگان ویکیپدیا. «Desargues's Theorem». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۸ سپتامبر ۲۰۱۹.
منابع
- Albert, A. Adrian; Sandler, Reuben (1968), An Introduction to Finite Projective Planes, New York: Holt, Rinehart and Winston
- Bamberg, John; Penttila, Tim (2015), "Completing Segre's proof of Wedderburn's little theorem", Bulletin of the London Mathematical Society, 47: 483–492, doi:10.1112/blms/bdv021
- Casse, Rey (2006), Projective Geometry: An Introduction, Oxford: Oxford University Press, ISBN 0-19-929886-6
- Coxeter, H.S.M. (1964), Projective Geometry, New York: Blaisdell
- Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR 0123930
- Cronheim, Arno (1953), "A proof of Hessenberg's theorem", Proceedings of the American Mathematical Society, 4: 219–221, doi:10.2307/2031794, MR 0053531
- Dembowski, Peter (1968), Finite Geometries, Berlin: Springer Verlag
- Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen, Berlin / Heidelberg: Springer, 61 (2): 161–172, doi:10.1007/BF01457558, ISSN 1432-1807
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), Chelsea, pp. 119–128, ISBN 0-8284-1087-9
- Hughes, Dan; Piper, Fred (1973), Projective Planes, Springer-Verlag, ISBN 0-387-90044-6
- Kárteszi, Ferenc (1976), Introduction to Finite Geometries, Amsterdam: North-Holland, ISBN 0-7204-2832-7
- Katz, Victor J. (1998), A History of Mathematics:An Introduction (2nd ed.), Reading, Mass.: Addison Wesley Longman, ISBN 0-321-01618-1
- Room, Thomas G.; Kirkpatrick, P. B. (1971), Miniquaternion Geometry, Cambridge: Cambridge University Press, ISBN 0-521-07926-8
- Smith, David Eugene (1959), A Source Book in Mathematics, New York: Dover, ISBN 0-486-64690-4
- Stevenson, Frederick W. (1972), Projective Planes, San Francisco: W.H. Freeman and Company, ISBN 0-7167-0443-9
- Voitsekhovskii, M.I. (2001), "Desargues assumption", in Hazewinkel, Michiel, دائرة المعارف ریاضیات, اشپرینگر ساینس+بیزینس مدیا, ISBN 978-1-55608-010-4
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.