قضیه مقدار میانی

در آنالیز ریاضی، قضیه مقدار میانی یا قضیه بولتسانو بیان می‌کند که برای هر تابع پیوسته ${\displaystyle f}$ روی بازهٔ ${\displaystyle [a,b]}$، به ازای هر مقدار ${\displaystyle u}$ که میان ${\displaystyle f(a)}$ و ${\displaystyle f(b)}$ و یا برابر آنان باشد، حداقل یک عدد مانند ${\displaystyle c}$ در بازه ${\displaystyle [a,b]}$ وجود دارد که ${\displaystyle f(c)=u}$. [1]

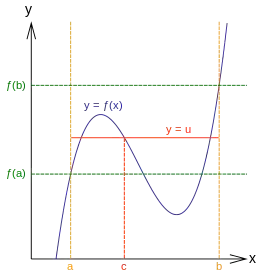
قضیهٔ مقدار میانی

حالتی از این قضیه نخستین بار توسط برنارد بولتسانو اثبات شد که برای وجود ریشه بین دو مقدار مثبت و منفی بیان می‌شود: اگر برای تابع ${\displaystyle f}$، پیوسته روی ${\displaystyle [a,b]}$، داشته‌ باشیم ${\displaystyle f(a)f(b)<0}$، آنگاه وجود دارد حداقل یک مقدار چون ${\displaystyle c\in [a,b]}$ به طوری که ${\displaystyle f(c)=0}$.[2]

قضیه ای با نام مشابه برای انتگرال ها وجود ندارد. این قضیه را نباید با قضیه مقدار میانگین اشتباه بگیریم.

جستارهای وابسته

• فضای همبند
• فضای توپولوژیک

پانویس

1. Protter and Protter, Calculus with Analytic Geometry, 206.
2. Eriksson , Estep and Johnson, Applied Mathematics: Body and Soul: Volume 1: Derivatives and Geometry in IR3, 216.

منابع

• Protter, M.H.; Protter, P.E. (1988). Calculus with Analytic Geometry. Jones and Bartlett. ISBN 978-0-86720-093-5. Retrieved 2015-05-09.
• Eriksson, K.; Estep, D.; Johnson, C. (2013). Applied Mathematics: Body and Soul: Volume 1: Derivatives and Geometry in IR3. SpringerLink: BĂźcher. Springer Berlin Heidelberg. ISBN 978-3-662-05796-4. Retrieved 2015-05-09.