قضیه پیک

چند ضلعی ای را بر روی نقاط صفحهٔ نقطه گذاری شده با فاصلهٔ مساوی می‌سازیم.یا به عبارت دیگر مختصات رئوس چند ضلعی عددی صحیح است.قضیهٔ پیک فرمولی است که با آن می‌توان مساحت چنین چند ضلعی ای را محاسبه کرد. این فرمول کار محاسبه را راحت می‌کند زیرا مساحت را بر اساس تعداد نقاط داخلی و تقاط روی محیط چند ضلعی می‌دهد.

i = 7

,

b = ۸

,

A = i + b / 2 - ۱ = ۱۰

The triangle with vertices at the lower left, lower right, and upper right points has

i = 12

and

b = 14

, giving by Pick's theorem

A = i + b / 2 - ۱ = 18

; this is confirmed by the triangle area formula ۱۲ × base × height = 12 × ۹ × ۴ = ۱۸.

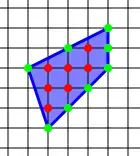
برای محاسبهٔ مساحت یک چند ضلعی به مساحت $A$ و نقاط داخلی $i$ و نقاط مرزی $b$ (نقاط روی اضلاع یا رئوس) فرمول زیر را داریم:[1]

A=i+{\frac {b}{2}}-1.

در مثال نشان داده شده هفت نقطه داخل چند ضلعی و هشت نقطه روی محیط آن قرار دارند ( $i = ۷$ و $b = ۸$ )پس:

$A$ = 7 + ۸/۲ − ۱ = ۷ + ۴ − ۱ = ۱۰

پس مساحت ۱۰ واحد مربع است.

قضیهٔ پیک تنها برای چندضلعی‌های ساده صادق است و برای چند ضلعی‌هایی که خود را قطع می‌کنند یا دارای حفره می‌باشند باید آن‌ها را به چند ضلعی‌های ساده تبدیل کرد و بعد مساحت را حساب کرد زیرا این فرمول مستقیماً روی چند ضلعی‌های غیر ساده درست عمل نمی‌کند.[2][3]

این فرمول اولین بار توسط گئورگ الکساندر پیک بیان شد. او در سال ۱۸۹۹ این فرمول را بیان کرد.[4] با کمک چهار وجهی ریو نشان داده‌اند که قضیهٔ پیک هیچ مشابهی در فضای سه بعدی ندارد. (فرمولی که با دانستن نقاط داخلی چند وجهی و نقاط روی سطح آن بتوان حجم آن چند وجهی را حساب کرد)

با این وجود Ehrhart polynomials تعمیمی از قضیهٔ پیک است که به فضاهایی با بعد بیشتر مربوط می‌شود.

اثبات

قضیه را با استفاده از استقرا اثبات می‌کنیم. چند ضلعی $P$ و مثلث $T$ را در نظر بگیرید به طوریکه $P$ و $T$ یک ضلع مشترک داشته باشند؛ و قضیه برای هر دو به تنهایی درست باشد.

می خولهیم نشان دهیم قضیه برای چندضلعی (که با اضافه کردن $T$ به $P$ به وجود می‌آید) نیز درست است.

از آنجایی که $P$ و $T$ یک ضلع مشترک دارند پس نقاط داخلی برابر می‌شود با نقاط داخلی $P$ و $T$ به اضافهٔ نقاط روی ضلع مشترک منهای دو (که آن دو نقطه نقاط ایتدا و انتهای ضلع مشترک هستند که روی مرز $PT$ قرار می‌گیرند) پس:[5]

i_{PT}=i_{P}+i_{T}+(c-2)

و همین‌طور:

b_{PT}=b_{P}+b_{T}-2(c-2)-2.

با ساده کردن عبارات بالا به نتایج زیر می‌رسیم:

i_{P}+i_{T}=i_{PT}-(c-2)

و

b_{P}+b_{T}=b_{PT}+2(c-2)+2.

از آنجایی که ما فرض کرده بودیم قضیه برای مثلث $T$ و چند ضلعی $P$ درست است پس:

{\begin{aligned}A_{PT}&=A_{P}+A_{T}\\&=\left(i_{P}+{\frac {b_{P}}{2}}-1\right)+\left(i_{T}+{\frac {b_{T}}{2}}-1\right)\\&=i_{P}+i_{T}+{\frac {b_{P}+b_{T}}{2}}-2\\&=i_{PT}-(c-2)+{\frac {b_{PT}+2(c-2)+2}{2}}-2\\&=i_{PT}+{\frac {b_{PT}}{2}}-1.\end{aligned}}

و نتیجه می‌گیریم قضیه برای $PT$ نیز برقرار است پس به حکم کلی زیر می‌رسیم:

اگر قضیه برای چندضلعی ساخته شده با $n$ مثلث درست باشد برای چند ضلعی ساخته شده با $n + 1$ مثلث نیز درست است؛ و واضح است که هر چند ضلعی را می‌توان به چند مثلث افراز کرد. برای اتمام اثبات استقرایی باید نشان دهیم که قضیه روی هر مثلثی نیز صادق است. این قسمت از اثبات را نیز با مراحل زیر انجام می‌دهیم.

اثبات می‌کنیم فرمول برای مربع واحد درست است. (طول و عرض راس‌های مربع باید عدد صحیح باشد)
سپس اثبات می‌کنیم که فرمول برای هر مستطیل با اضلاع موازی با محورها نیز درست است.
حالا با نصف کردن مستطیل از قطرش و تبدیل آن به مثلث قائم الزاویه اثبات می‌کنیم که قضیه برای مثلث‌های قائم الزاویه نیز درست است.
حالا با توجه به این که هر مثلث با شرایط قضیه را می‌توان به چند مثلث قائم الزاویه تبدیل کرد ثابت می‌کنیم قضیه برای هر مثلثی صادق است.

و بدین ترتیب قضیه اثبات می‌شود.

جستارهای وابسته

Integer points in convex polyhedra
Steinhaus longimeter
Farey sequence

منابع

Trainin, J. (November 2007). "An elementary proof of Pick's theorem". Mathematical Gazette. 91 (522): 536–540. doi:10.1017/S0025557200182270.
Garbett, Jennifer (November 18, 2010). "Lattice Point Geometry: Pick's Theorem and Minkowski's Theorem, Senior Exercise in Mathematics" (PDF). Archived from the original (PDF) on 29 Aug 2017.
Belyaev, Alexander; Fayolle, Pierre-Alain (2019-08-08). "Counting Parallel Segments: New Variants of Pick's Area Theorem". The Mathematical Intelligencer. 41 (4): 1–7. doi:10.1007/s00283-019-09921-8. ISSN 0343-6993.
Pick, Georg (1899). "Geometrisches zur Zahlenlehre". Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen "Lotos" in Prag. (Neue Folge). 19: 311–319. JFM 33.0216.01. CiteBank:47270
Beck, Matthias; Robins, Sinai (2007). Computing the Continuous Discretely: Integer-point enumeration in polyhedra. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ch. 2. ISBN 978-0-387-29139-0. MR 2271992.

پیوند به بیرون

Pick's Theorem (Java) at cut-the-knot
Pick's Theorem
Pick's Theorem proof by Tom Davis
Pick's Theorem by Ed Pegg, Jr. , the Wolfram Demonstrations Project.
Weisstein, Eric W. "Pick's Theorem". MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Trainin, J. (November 2007). "An elementary proof of Pick's theorem". Mathematical Gazette. 91 (522): 536–540. doi:10.1017/S0025557200182270.

[:0-2] Garbett, Jennifer (November 18, 2010). "Lattice Point Geometry: Pick's Theorem and Minkowski's Theorem, Senior Exercise in Mathematics" (PDF). Archived from the original (PDF) on 29 Aug 2017.

[3] Belyaev, Alexander; Fayolle, Pierre-Alain (2019-08-08). "Counting Parallel Segments: New Variants of Pick's Area Theorem". The Mathematical Intelligencer. 41 (4): 1–7. doi:10.1007/s00283-019-09921-8. ISSN 0343-6993.

[4] Pick, Georg (1899). "Geometrisches zur Zahlenlehre". Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen "Lotos" in Prag. (Neue Folge). 19: 311–319. JFM 33.0216.01. CiteBank:47270

[5] Beck, Matthias; Robins, Sinai (2007). Computing the Continuous Discretely: Integer-point enumeration in polyhedra. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ch. 2. ISBN 978-0-387-29139-0. MR 2271992.