مسئله ازدواج پایدار
مسئله ازدواج پایدار در ریاضیات برای مدلسازی تطابق پایدار به کار میرود.
تعریف
بهطور کلی این قضیه بیانگر این است که اگر مجموعهای از مردها و مجوعهای از زنها داشته باشیم که هر یک دارای اولویتهایی برای ازدواج باشند، در این راستا حتماً راهی وجود داردکه در نهایت امکان ندارد دو نفر که یکدیگر را میخواهند (در واقع در اولویت یکدیگر هستند) با یکدیگر نباشند. این راه از طریق الگوریتم گیل-شاپلی پیدا میشود. توجه کنید که طبق این الگوریتم حتماً راهی وجود دارد که شرایط بالا را داشته باشد.
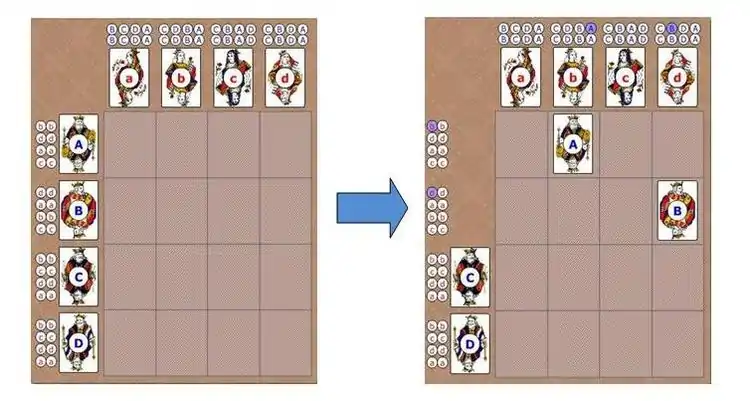
در شکل روبه رو: ۴ مرد (شاه) و ۴ زن (ملکه) وجود دارند. برای مثال مرد A زنها را با ترتیب C , A، D , B امتیاز دهی کردهاست و به همان صورت زن B مردها را با ترتیب A , B، D , C ترجیح میدهد.
الگوریتم
در سال ۱۹۶۲ دیوید گیل و لوید شاپلی اثبات کردند که برای هر تعداد مساوی زن و مرد، میتوان مسئلهٔ ازدواج پایدار را حل کرد و الگوریتمی برای این کار ارائه دادند. هدف از اجرای این الگوریتم آن است که راهی پایدار برای تطبیق دادن و جفت کردن مردان با زنان (با توجه به اولویتهای آنها) بیابیم. مرتبه زمانی این الگوریتم (O(n2 میباشد.
انتخابهای ناپایدار
راهی ناپایدار است که در آن مرد و زنی وجود داشته باشند که با یکدیگر جفت نشدهاند اما یکدیگر را به جفتهای فعلی خود ترجیح دهند.
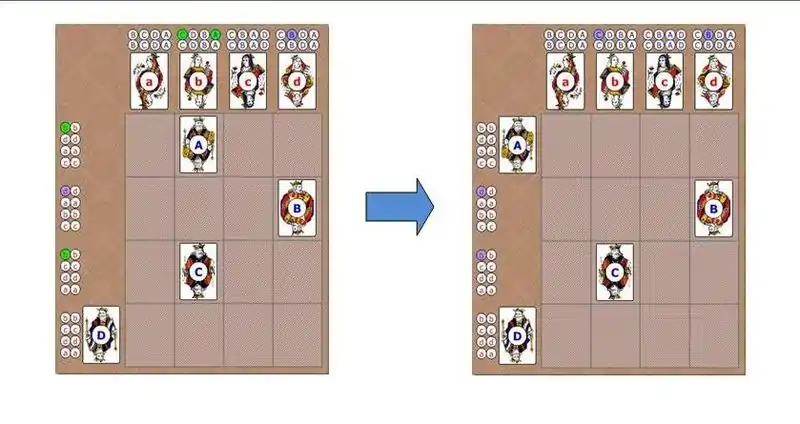
همانطور که میبینیم این یک انتخاب ناپایدار است. به مرد C و زن B نگاه کنید. هر دوی آنها یکدیگر را به جفتهای فعلی خود ترجیح میدهند. مرد C با انتخاب دوم خود جفت شده و زن B با انتخاب سوم خود، در حالی که اگر این دو با هم جفت میشدند هر دو به انتخاب اول خود میرسیدند. قلبها نشان دهندهٔ بیثبات بودن انتخابهای کنونی میباشند.
توضیح الگوریتم گیل-شاپلی
پیدا کردن راهی پایدار برای جفت کردن مردها و زنها نیازمند آزمایشهای متعدد است که گاه زمان زیادی میبرد اما الگوریتم گیل-شاپلی راه حلی را برای یک انتخاب پایدار ارائه میکند. این الگوریتم بیانگر این است که بدون توجه یه تعداد مردها و زنها، همواره میتوان راهی پایدار برای جفت کردن آنها پیدا کرد. طرز کار این الگوریتم به صورت زیر است: ابتدا هر مرد از اولویت اول خود درخواست میکند، اگر زن مورد نظر قبلاً با کسی «نامزد» نشده باشد این درخواست را قبول میکند اما اگر فرد دیگری نیز از او درخواست کرده بود، زن شخصی را برمیگزیند که اولویت بالاتری نسبت به فرد دیگر دارد. مردی که درخواستش رد شدهاست از این درخواست صرف نظر کرده و درخواست دیگری را به اولویت بعدی خود مطرح میکند. در مثال زیر این روش مشخص تر است:
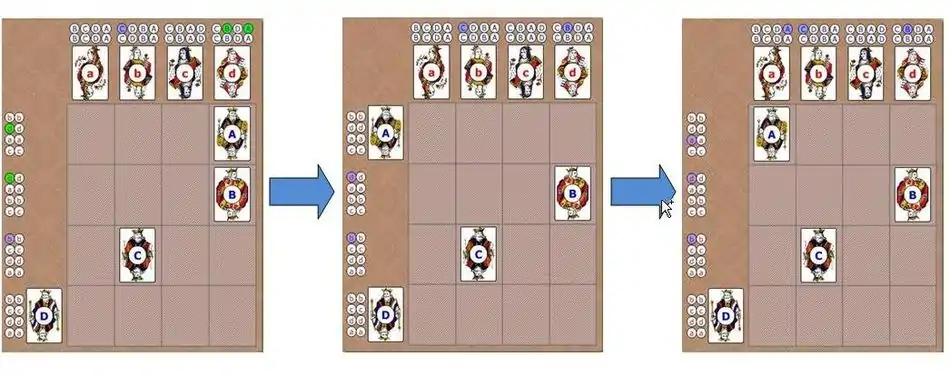
در قدم اول مردهای A و B از زنهایی که در اولویت اول هستند درخواست میکنند و طبق الگوریتم اگر زن درخواست دیگری نداشته باشد خود به خود این درخواست را قبول میکند؛ بنابراین مرد A از زن B و مرد B از زن D درخواست میکند و آنها نیز این درخواست را میپذیرند. در مرحلهٔ بعدی نوبت مرد C است که درخواست خود را مطرح کند. زن B در اولویت اول مرد C قرار دارد بنابراین مرد C از وی درخواست میکند، اما زن B نامزد شدهاست پس طبق الگوریتم زن باید مردی را انتخاب کند که امتیاز بالاتری نسبت به دیگری دارد. طبق این دستورالعمل زن B مرد C را که اولویت اول خودش است، انتخاب میکند و مرد A مجبور است انتخاب دیگری بکند:
در قدم بعدی، مرد A باید انتخاب بعدی خود را طبق اولویتهایش مطرح کند که در اینجا اولویت دوم او زن D است. اما مانند حالت قبل زن D نامزد شدهاست بنابراین باید یکی از دو مرد A یا B را انتخاب کند که چون مرد B برای زن دارای امتیاز بالاتری است، انتخاب میشود و به این ترتیب مرد C باید به سراغ اولویت بعدی خود یعنی زن A برود:
زن A هیچ درخواست دیگری ندارد بنابراین این پیشنهاد را میپذیرد. در مرحلهٔ بعد، نوبت مرد D است که انتخاب خود را انجام دهد. همانطور که میبینیم اولویت اول او، زن B است اما از آن جا که زن B نامزد شدهاست مانند حالت قبل باید یکی از مردها را انتخاب کند که در اینجا به علت اولویتهای زن B، مرد D رد میشود و باید از اولویت بعدی خود یعنی زن C درخواست کند:
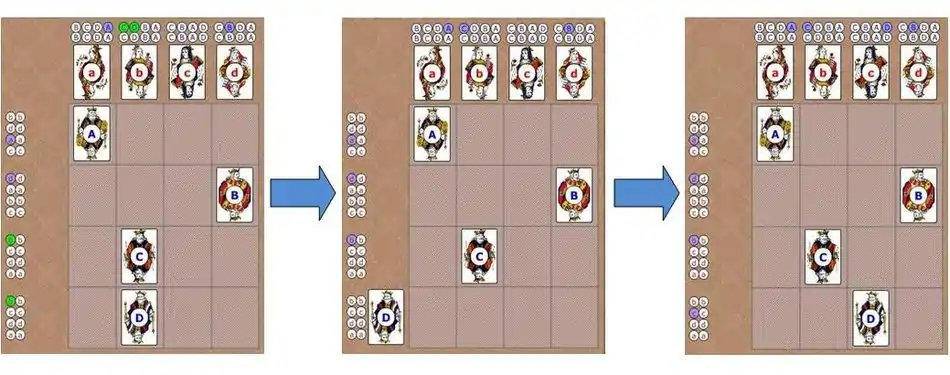
زمانی که همهٔ مردها با زنی جفت شوند آنگاه مسئله به پایان رسیدهاست و راه پایدار برای آن پیدا شدهاست. همانطور که مشخص است طبق هدف این الگوریتم هیچ مرد و زنی نیستند که با وجود بیشتر خواستن فرد دیگری با شخصی دیگر جفت شده باشند.
نکته
در این روش، ترتیب انتخاب مردان مهم نیست. آنها میتوانند با هم انتخاب کنند و اگر کسانی باید جواب رد میگرفتند، در مرحلهٔ بعدی همه با هم به انتخابهای بعدی بپردازند. این روش که یک زیر شاخه از الگوریتم گیل-شاپلی است به الگوریتم McVitie-Wilson معروف میباشد.
کاربرد
در دنیای واقعی، الگوریتم گیل-شاپلی برای فرستادن دانشجویان پزشکی به بیمارستان مورد علاقهٔ آنها، حل برخی مسائل گرافهای وزن دار (برای مثال پیدا کردن کم خرجترین مسیر در یک گراف وزن دار)، تقسیم دانشجویان در اتاقهای خوابگاه و … به کار میرود.
منابع
- <http://mathsite.math.berkeley.edu / منبع عکس ها>
- <http://www.glossary.com/encyclopedia.php?q=Gale-Shapley_algorithm%5Bپیوند+مرده%5D>
- <http://math-sci.iranjournals.ir/article_14168_0.html / مقالهای دربارهٔ نظریه جورساز پایدار در مجله ریاضی و جامعه>