معمای مربع گم‌شده

معمای مربع گم‌شده معمایی متأثر از خطای دید است که در کلاس‌های درس ریاضیات به منظور به کارگیری تجسم هندسی دانش‌آموزان مطرح می‌شود.
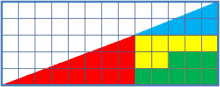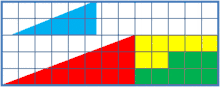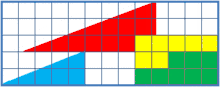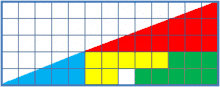
این پازل دو ترکیب از اشکالی را نشان می‌دهد که ظاهراً در مجموع، دو مثلث قائم‌الزاویهٔ هم‌نهشت هستند. اما یکی از آن‌ها یک مربع ۱×۱ فضای خالی دارد.

به مربع خالی توجه کنید

پاسخ

تفاوت دو ترکیب

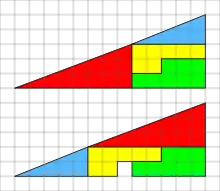
دلیل به وجود آمدن مربع خالی این است که برخلاف فرض بیننده، هیچ‌کدام از دو شکلِ به‌ظاهر مثلثِ به دست آمده، مثلث نیستند و در واقع چهارضلعی هستند و این دو چهارضلعی نیز با هم همنهشت نیستند و البته چشم طبیعی انسان قادر به تشخیص این تفاوت نمی‌باشد. نسبت اضلاع قائم مثلث قرمز ۸:۳ و این نسبت در مثلث آبی‌رنگ ۵:۲ است که در نتیجه وتر مثلث‌ها شیب یکسانی نخواهند داشت و یک درجه با هم فرق دارند. خط حاصل از امتداد این دو نیز یک خط راست تشکیل نمی‌دهد. به علت کوچک بودن تفاوت شیب دو خط، چشم انسان معمولاً قادر به تشخیص این اختلاف نیست.

معماهای مشابه

معمای مربع گم‌شده

نسخهٔ دیگری از این معما به چهار چهارضلعی و یک مربع کوچک در میان آن‌ها مربوط می‌شود که در کنار هم مربع بزرگ‌تری می‌سازند. هنگامی که چهارضلعی‌ها می‌چرخند فضای مربع کوچک را پر می‌کنند ولی به نظر می‌رسد مربع بزرگ بدون تغییر مانده است.

تجزیه سم لوید

مساحت مربع از مساحت مستطیل یک واحد کمتر است!

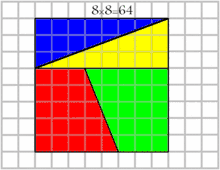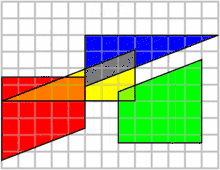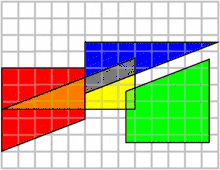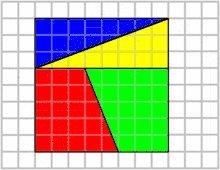
چهار قطعه با مجموع مساحت ۶۴ در کنار هم قرار گرفته‌اند ولی بعد از جابه‌جایی ۱ واحد به مساحت آن‌ها اضافه می‌شود در حالی که قطعات تغییری نکرده‌اند پس مساحت کل هم نباید تغییر می‌کرد!

علت این پدیده، شیب متفاوت قطعه‌ها است، برای مثال قطعه آبی و سبز در حالت دوم هم‌پوشانی دارند و قسمتی از هر کدام با هم منطبق می‌شوند. شیب وتر قطعه آبی برابر ۰٫۳۷۵ است که روی ضلعی از قطعه سبز قرار می‌گیرد که شیب آن ۰٫۴ است. نزدیکی شیب‌ها باعث می‌شود این تفاوت در نگاه اول نمایان نشود. برای درک بهتر کافیست شکل را روی کاغذ رسم کنید و قطعات را پس از برش جابه‌جا کنید.

این دوحالت با یک واحد اختلاف همیشه سه جمله ی متوالی دنباله ی فیبوناتچی را نشان میدهند که یکی از حالات ضرب دوجمله ی ${\displaystyle a_{n-1}}$ و ${\displaystyle a_{n+1}}$ و دیگری برابر ${\displaystyle (a_{n})^{2}}$ است. به عنوان مثال شکل روبرو دوحالت ${\displaystyle 5\times 13=65}$ و ${\displaystyle 8\times 8=64}$ که حاصل سه جمله ی متوالی دنباله ی فیبوناتچی هستند.

منابع

در ویکی‌انبار پرونده‌هایی دربارهٔ معمای مربع گم‌شده موجود است.

• مشارکت‌کنندگان ویکی‌پدیا. «Missing square puzzle». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۲ ژوئیه ۲۰۱۰.