میانه میانه‌ها

در علوم رایانه، میانهٔ میانه‌ها یک الگوریتم انتخاب بر پایهٔ الگوریتم انتخاب سریع می‌باشد. این الگوریتم، بهینه و در بدترین حالت ممکن برای انتخاب k امین عضو بزرگ یک مجموعه دارای عملکردی خطی می‌باشد. این الگوریتم میانهٔ تقریبی را در مدت زمانی خطی بدست آورده و به عنوان عنصر محوری در اختیار الگوریتم انتخاب سریع قرار می‌دهد.

میانه میانه‌ها

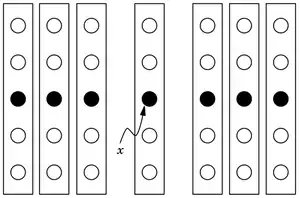میانه انتخابی بین 30 تا 70 درصدی داده‌هاست
رده	الگوریتم انتخاب
ساختمان داده	آرایه
کارایی بدترین حالت	${\displaystyle O(n)}$
کارایی بهترین حالت	${\displaystyle O(n)}$
پیچیدگی فضایی	${\displaystyle O(logn)}$ (سرشکن)

این الگوریتم می‌تواند به عنوان یک روش برای پیدا کردن عنصر محوری در مرتب‌سازی سریع مورد استفاده قرار گرفته و به یک الگوریتم مرتب‌سازی بهینه با عملکرد در بدترین حالت از ${\displaystyle O(nlogn)}$ منجر شود. اگرچه این روش بهینه است، اما در عمل برای از بین بردن سربار محاسبهٔ عنصر محوری؛ این عنصر معمولاً به صورت تصادفی انتخاب می‌شود. میانه میانه‌ها به عنوان یک بازگشت در الگوریتم انتخاب درونگرا مورد استفاده قرار می‌گیرد تا عملکرد بدترین حالت را بهبود بخشد: انتخاب درونگرا با انتخاب سریع شروع می‌شود تا یک عملکرد متوسط را نتیجه دهد، سپس در صورتی که روند اجرا بسیار کند باشد، از میانه میانه‌ها استفاده می‌کند.

این الگوریتم توسط Blum et al. (1973) منتشر شد و به همین دلیل برخی از مواقع با نام BFPRT (حروف اول اسم ناشران آن) شناخته می‌شود. در مقالهٔ اصلی از این الگوریتم به اسم PICK و از الگوریتم انتخاب سریع به عنواد FIND یاد شده است.

چکیده

زمان لازم برای انتحاب سریع به طور میانگین به صورت خطی رشد می‌کند، اما با انتخاب نامناسب عنصر محوری می‌تواند به صورت درجهٔ دو رشد کند. دلیل این امر این است که انتخاب سریع، یک الگوریتم تقسیم و حل است که هر مرحلهٔ آن زمانی از ${\displaystyle O(n)}$ روی باقیماندهٔ اعضا لازم دارد. اگر اندازهٔ مجموعه‌ای که الگوریتم انتخاب سریع روی آن جستجو انجام می‌دهد سریع و به صورت نمایی کاهش یابد (با نسبتی ثابت)، منجر به یک سری هندسی با زمانی از ${\displaystyle O(n)}$ خواهد شد و در نتیجه در طول زمان به صورت خطی رفتار خواهد کرد. حال اگر اندازهٔ این مجموعه با سرعتی آهسته کم شود، مثلاً به صورت خطی (در بدترین حالت در هر مرحله تنها یک عضو از مجموعه کاسته می‌شود)، جمع تمامی مراحل منجر به زمانی از ${\displaystyle O(n^{2})}$ خواهد شد. بدترین حالت، زمانی رخ می‌دهد که کوچکترین عضو مجموعه در هر مرحله به عنوان عنصر محوری انتخاب شود (برای مثال حالتی که برای انتخاب بزرگترین عضو یک مجموعه مرتب شده از انتخاب سریع استفاده شود و در هر مرحله اولین عضو مجموعه را به عنوان عنصر محوری در نظر بگیریم).

اگر به صورت پیاپی عناصر محوری خوبی را انتخاب نماییم همواره زمان اجرایی خطی را حتی در بدترین حالت ممکن خواهیم داشت. عنصر محوری خوب، عنصری است که همواره درصد ثابتی از اعضای مجموعه قبل و بعد از آن وجود داشته باشند تا در هر مرحله تعداد اعضای باقیمانده در مجموعه به صورت نمایی کاهش یابد. میانه همیشه یک عنصر محوری خوب محسوب می‌شود (بهترین گزینه برای مرتب‌سازی و یکی از بهترین گزینه‌ها برای انتخاب).

الگوریتم میانه میانه‌ها، میانه را نه به صورت دقیق، بلکه به صورت تقریبی محاسبه می‌کند. اما این تضمین را می‌دهد که مقدار محاسبه شده بین ۳۰امین و ۷۰امین صدک قرار گرفته باشد؛ بنابراین در هر مرحله تعداد داده‌ها حداقل ۳۰٪ کاهش می‌یابد.

الگوریتم

همان‌طور که ذکر شد، میانه میانه‌ها به عنوان یک راه‌حل برای انتخاب عنصر محوری در الگوریتم انتخاب سریع مورد استفاده قرار می‌گیرد و شبه کد آن به صورت زیر است:

function select(list, left, right, n)
    if left = right
        return left
    loop
        pivotIndex := pivot(list, left, right)
        pivotIndex := partition(list, left, right, pivotIndex)
        if n = pivotIndex
            return n
        else if n < pivotIndex
            right := pivotIndex - 1
        else
            left := pivotIndex + 1

همانند انتخاب سریع در الگوریتم میانه میانه‌ها نیز یک زیر رَویه به نام «تقسیم کننده» وجود دارد که می‌تواند یک لیست را به دو بخش (اعضای کوچکتر از یک عنصر خاص و اعضای بزرگتر از آن) تقسیم کند. شبه کد یک تقسیم‌کننده که یک تقسیم بر پایهٔ [list[pivotindex انجام می‌دهد را در زیر می‌توانید مشاهده کنید:

 function partition(list, left, right, pivotIndex)
     pivotValue := list[pivotIndex]
     swap list[pivotIndex] and list[right]  // Move pivot to end
     storeIndex := left
     for i from left to right-1
         if list[i] < pivotValue
             swap list[storeIndex] and list[i]
             increment storeIndex
     swap list[right] and list[storeIndex]  // Move pivot to its final place
     return storeIndex

تابع pivot بخش اصلی الگوریتم میانه میانه‌هاست. این تابع ورودی (یک لیست به طول n) را به گروه‌هایی با پنج عضو تقسیم کرده و میانهٔ هر گروه را محاسبه می‌کند. سپس به صورت بازگشتی میانهٔ اصلی n5 میانه‌های بدست آمده در قسمت قبل را بدست می‌آورد:[1]

  function pivot(list, left, right)
     // for 5 or less elements just get median
     if right - left < 5:
         return partition5(list, left, right)
     // otherwise move the medians of five-element subgroups to the first n/5 positions
     for i from left to right in steps of 5
         // get the median of the i'th five-element subgroup
         subRight := i + 4
         if subRight > right:
             subRight := right

         median5 := partition5(list, i, subRight)
         swap list[median5] and list[left + floor((i - left)/5)]

     // compute the median of the n/5 medians-of-five
     return select(list, left, left + ceil((right - left) / 5) - 1, left + (right - left)/10)

تابع partition5 میانهٔ یک گروه با حداکثر پنج عضو را انتخاب می‌کند. یک راه ساده برای پیاده‌سازی این تابع استفاده از مرتب‌سازی درجی است.[1]

در نهایت می‌توان عمکرد الگوریتم میانه میانه‌ها را به ۵ مرحله تقسیم کرد:

مرحله ۱: تمامی n عضو به گروه‌های ۵ تایی دسته بندی می‌شوند. (در صورتی که تعداد عضو‌ها به ۵ قابل قسمت نباشد گروه آخر کمتر از ۵ عضو را در خود جای می‌دهد.)

مرحله ۲: میانه هر یک از n5 گروه‌های ایجاد شده پیدا می‌شوند. (ابتدا هر یک از این گروه ها در ${\displaystyle o(1)}$ مرتب شده و سپس میانۀ آنها انتخاب می‌شود.)

مرحله ۳: به صورت بازگشتی میانه n5 داده ها انتخاب می‌شود.

مرحله ۴: با استفاده از تابع پارتیشن که میانۀ انتخابی را به عنوان عنصر محوری در ورودی دریافت می‌کند، با فرض اینکه میانۀ انتخابی k امین کوچکترین عضو باشد، داده ها به دو دستۀ k - 1 تایی و n - k تایی تقسیم می‌شوند که تمامی اعضای آنها به ترتیب کوچکتر و بزرگتر از میانۀ انتخابی است.

مرحله ۵: در این مرحله ۳ حالت وجود دارد:

اگر اندیس میانۀ انتخابی برابر i باشد: این عضو به عنوان جواب بازگردانده می‌شود.

اگر اندیس میانۀ انتخابی بزرگتر از i باشد: i امین کوچکترین عضو در بین داده‌های کوچکتر از میانه به عنوان جواب بازگردانده می‌شود.

اگر اندیس میانۀ انتخابی کوچکتر از i باشد: i - k امین کوچکترین عضو در بین داده‌های بزرگتر از میانه به عنوان جواب بازگردانده می‌شود.

ویژگی‌های عنصر محوری

از n۵ گروه‌ها، نیمی از آنها (n۱۰=n۵×½) میانه‌هایی کمتر از میانهٔ واقعی (میانه میانه‌ها) و نیمی دیگر از آنها میانه‌هایی بیشتر از آن دارند. در هر یک از n۱۰ گروه‌ها با میانهٔ کمتر از میانهٔ واقعی، ۲ عضو کوچکتر از میانهٔ گروه خود هستند؛ بنابراین در n۱۰ از گروه‌ها حداقل ۳ عضو کوچکتر از میانهٔ اصلی هستند. به صورت مشابه در n۱۰ دیگر از گروه‌ها با میانهٔ بزرگتر از میانهٔ اصلی حداقل ۲ عضو وجود دارند که از میانهٔ گروه خود بزرگتر هستند و در نتیجه n۱۰ از گروه‌ها دارای حداقل ۳ عضو بزرگتر از میانهٔ اصلی هستند؛ بنابراین میانهٔ اصلی حداقل از n۱۰×۳ داده‌ها بیشتر و از n۱۰×۳ آنها کمتر است؛ بنابراین میانهٔ انتخاب شده بین ۳۰٪ تا ۷۰٪ داده‌ها است:

یکی از مراحل روی ۱۰۰ دادهٔ تصادفی از ۰ تا ۹۹

	۱۲		۱۵		۱۱		۲		۹		۵		۰		۷		۳		۲۱		۴۴		۴۰		۱		۱۸		۲۰		۳۲		۱۹		۳۵		۳۷		۳۹
	۱۳		۱۶		۱۴		۸		۱۰		۲۶		۶		۳۳		۴		۲۷		۴۹		۴۶		۵۲		۲۵		۵۱		۳۴		۴۳		۵۶		۷۲		۷۹
میانه‌ها	۱۷		۲۳		۲۴		۲۸		۲۹		۳۰		۳۱		۳۶		۴۲		۴۷		۵۰		۵۵		۵۸		۶۰		۶۳		۶۵		۶۶		۶۷		۸۱		۸۳
	۲۲		۴۵		۳۸		۵۳		۶۱		۴۱		۶۲		۸۲		۵۴		۴۸		۵۹		۵۷		۷۱		۷۸		۶۴		۸۰		۷۰		۷۶		۸۵		۸۷
	۹۶		۹۵		۹۴		۸۶		۸۹		۶۹		۶۸		۹۷		۷۳		۹۲		۷۴		۸۸		۹۹		۸۴		۷۵		۹۰		۷۷		۹۳		۹۸		۹۱

عنصر قرمز رنگ: میانه میانه‌ها، عناصر خاکستری: اعداد کوچکتر از میانه میانه‌ها، عناصر سفید: عناصر بزرگتر از میانه میانه‌ها

۵ تایی‌های بالا برای وضوح بیشتر به صورت مرتب شده نمایش داده شده‌اند. اما در واقع، از آنجایی که ما تنها به دنبال میانهٔ این ۵ تایی‌ها هستیم مرتب بودن آنها اهمیتی ندارد.

توجه کنید که تمامی عناصر بالا-راست عنصر قرمز رنگ(۳۰٪ کل عناصر) کوچکتر از آن و تمامی عناصر پایین-چپ این عنصر(۳۰٪ کل عناصر)، بزرگتر از آن هستند.

زمان اجرا

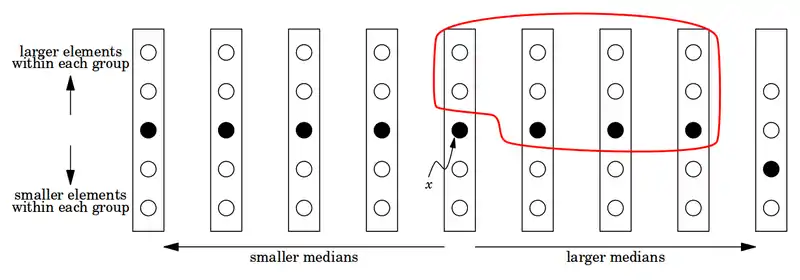
همانطور که در تصویر بالا مشاهده می‌کنید، به جز گروهی که شامل میانۀ انتخابی (x) است و گروه آخر، در نیمی دیگر از گروه‌ها حداقل ۳ عضو وجود دارد که از x کوچکتر هستند. (این ۳ عضو شامل میانه‌های کوچکتر از x و دو عضو کوچکتر از هر میانه، در هر یک از n5 گروه‌ها است) بنابراین:

${\displaystyle {\text{elts less than }}x\geqslant 3(\left\lceil {\frac {1}{2}}\left\lceil {\frac {n}{5}}\right\rceil \right\rceil -2)\geqslant {\frac {3n}{10}}-6}$

به صورت مشابه حداقل 6 - 3n10 عضو بزرگتر از x هستند. بنابراین مرحله‌ ۵ام حداکثر روی 6 + 3n10 از داده‌ها بازگشت می‌کند. از طرفی، مراحل ۱، ۲ و ۴ برای اجرا شدن احتیاج به زمانی از ${\displaystyle O(n)}$ دارند.‌ ( مرحله ۱: ایجاد گروه‌های با ۵ عضو احتیاج به زمانی از ${\displaystyle O(n)}$ دارد، مرحله ۲: مرتب سازی هر گروه ۵ تایی احتیاج به زمانی از ${\displaystyle O(1)}$ و مرحله ۴: تقسیم کردن داده ها حول میانه انتخابی احتیاح به زمانی از ${\displaystyle O(n)}$ دارد.) مرحله ۳ زمانی از ${\displaystyle T({\frac {n}{5}})}$ را احتیاج داشته و مرحله آخر زمانی کمتر از ${\displaystyle T({\frac {7n}{10}}+6)}$ را برای اجرا لازم دارد. با فرض اینکه با n های به قدر کافی کوچک زمان اجرا از ${\displaystyle O(1)}$ باشد، میتوان گفت: (n را به دلیلی که مشاهده خواهید کرد حداقل برابر 140 در نظر می‌گیریم)

${\displaystyle T(n)\leq {\begin{cases}O(1),&{\text{if }}n<140\\T(\left\lceil {\frac {n}{5}}\right\rceil )+T({\frac {7n}{10}}+6)+O(n),&{\text{if }}n\geq 140\end{cases}}}$

با در نظر گرفتن ${\displaystyle T(n)\leq c\cdot n}$ به عنوان فرض استقرا می‌توان نوشت:

${\displaystyle T(n)\leq c\cdot \left\lceil {\frac {n}{5}}\right\rceil +c\cdot ({\frac {7n}{10}}+6)+an}$

${\displaystyle \Rightarrow T(n)\leq {\frac {cn}{5}}+c+{\frac {7cn}{10}}+6c+an}$

${\displaystyle \Rightarrow T(n)\leq {\frac {9cn}{10}}+7c+an}$

${\displaystyle \Rightarrow T(n)\leq cn+(-{\frac {cn}{10}}+7c+an)}$

در صورتی که جملۀ ${\displaystyle (-{\frac {cn}{10}}+7c+an)}$ کوچکتر از صفر باشد فرض استقرا برقرار می‌شود و به سادگی میتوان متوجه شد که به ازای ${\displaystyle c\geq 10a\cdot {\frac {n}{n-70}}}$، این جمله کوچکتر از صفر شده و از آنجایی که n از ۱۴۰ بزرگتر است، ${\displaystyle {\frac {n}{n-70}}}$ همواره کمتر مساوی ۲ بوده و به همین دلیل به ازای ${\displaystyle c\geq 20a}$ خواهیم داشت:

${\displaystyle T(n)\leq {\begin{cases}O(1),&{\text{if }}n<140\\O(n),&{\text{if }}n\geq 140{\text{ and }}c\geq 20a\end{cases}}}$

منابع

1. مقدمه‌ای بر الگوریتم‌ها

• M. Blum, R.W. Floyd, V. Pratt, R. Rivest and R. Tarjan, "Time bounds for selection," J. Comput. System Sci. 7 (1973) 448-461.
• توماس اچ کورمن، Charles E. Leiserson, رونالد ریوست، and کلیفورد استین. مقدمه‌ای بر الگوریتم‌ها, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 9: Medians and Order Statistics, pp. 183–196. Section 14.1: Dynamic order statistics, pp. 302–308.

پیوند به بیرون

• "Lecture notes for January 30, 1996: Deterministic selection", ICS 161: Design and Analysis of Algorithms, David Eppstein