چندجمله‌ای چبیشف

چندجمله‌ای‌های چبیشف یک دنباله از چندجمله‌ای‌های متعامد هستند که به طرز بازگشتی محاسبه می‌شوند. نام این چندجمله‌ای‌ها از نام ریاضی‌دان روس پافنوتی چبیشف برگرفته شده که آن‌ها را اولین بار در سال ۱۸۵۴ معرفی کرد.

تاریخ

پافنوتی چبیشف ریاضی‌دان روس متولد ۱۶ مه سال ۱۸۲۱ بود. چندجمله‌ای‌های چبیشف که به نام او شناخته می‌شوند، است یک توالی از چندجمله‌ایهای@12@ متعامد هستند که می توان آنها را مثل فیبوناچی به صورت برگشت پذیر نوشت. این چندجمله‌ای‌ها دو نوع اول و دوم دارند که نوع اول آن‌ها با T و نوع دوم آن‌ها با U نشان داده می‌شوند. علت نام گذاری T این است که chebyshev به زبان فرانسوی Tchebyshev و به زبان آلمانی Tschebyschow می باشد.

کاربرد

چندجمله ایهای چبیشف بیشتر در تخمین کاربرد دارند و استفاده از آنها برای تخمین به مقدار زیادی خطا را کاهش می دهد. مثلاً در اندازه گیری طول یک نیم دایره و اشکال دارای قوس.

مقدمه

کسینوسها:

از رابطه ی زیر شروع می کنیم:

${\displaystyle cos((n+1)\theta )=2cos(\theta )cos(n\theta )-cos((n-1)\theta )(1)}$

که با ۲ بار استفاده از فرمول زیر محاسبه می شود.

${\displaystyle cos(\alpha +\beta )=cos\alpha cos\beta -sin\alpha sin\beta }$

سپس ادعا میکنیم که به ازای هر عدد صحیح مثبت n اعداد صحیح ci وجود دارند به طوری که:

${\displaystyle cosn\theta =\sum _{i=0}^{n}c_{i}cos^{i}(\theta )(2)}$

تعریف: رابطه ی 2 می گوید که (cos(nθ یک چندجمله ای برحسب (cos(θ است.برای n ثابت n امین چندجمله ای چبیشف به صورت زیر تعریف می شود:

${\displaystyle cos(n\theta )=Tn(cos\theta )(3)}$

که اگر (x = cos(θ باشد:

${\displaystyle T_{n}(x)=cos(narccos(x))(4)}$

برای x های بین 1 و 1-

در واقع چندجمله ای های چبیشف نمودارهای کسینوسی هستند که مقیاس افقی آنها تغییر کرده ولی مقیاس عمودی آنها نه.و ریشه های آن که به آنها گره هم می گویند زمانی است که(cos(θ صفر شود یعنی (برای n های طبیعی) :

${\displaystyle x=cos({\frac {(2i-1)\pi }{2n}})}$

با توجه به روابط بالا به این رابطه ی بازگشتی می رسیم:

${\displaystyle T_{0}(x)=1,T_{1}(x)=x(5)}$

${\displaystyle x=cos\theta }$

${\displaystyle T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x)(6)}$

جوابهای معادله ی 6 با مقدارهای اولیه داده شده در 5 چندجمله ایهای چبیشف نوع اول را نتیجه می دهد.

مثال‌ها

اولین چندجمله‌ای‌های نوع اول چبیشف به صورت زیر می‌باشند:

منحنی‌های مربوط به اولین چندجمله‌ای‌های نوع اول چبیشف بر روی دامنه −1¼ < x < 1¼, −1¼ < y < 1¼; the flat T₀, and T₁, T₂, T₃, T₄ and T₅.

${\displaystyle T_{0}(x)=1\,}$

${\displaystyle T_{1}(x)=x\,}$

${\displaystyle T_{2}(x)=2x^{2}-1\,}$

${\displaystyle T_{3}(x)=4x^{3}-3x\,}$

${\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1\,}$

${\displaystyle T_{5}(x)=16x^{5}-20x^{3}+5x\,}$

${\displaystyle T_{6}(x)=32x^{6}-48x^{4}+18x^{2}-1\,}$

${\displaystyle T_{7}(x)=64x^{7}-112x^{5}+56x^{3}-7x\,}$

${\displaystyle T_{8}(x)=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\!}$

${\displaystyle T_{9}(x)=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x.\,}$

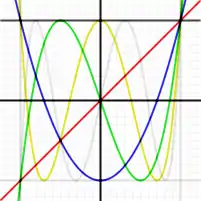
ملاحظات

شایان توجه است که این چندجمله‌ایها همان بسط کسینوس مضارب صحیح و غیر منفی زوایا هستند. یعنی:

${\displaystyle cos2\alpha =2cos^{2}\alpha -1\!}$

${\displaystyle cos3\alpha =4cos^{3}\alpha -3cos\alpha \!}$

${\displaystyle cos4\alpha =8cos^{4}\alpha -8cos^{2}\alpha +1\!}$

منحنی‌های مربوط به اولین چندجمله‌ای‌های نوع دوم چبیشف بر روی دامنه −1¼ < x < 1¼, −1¼ < y < 1¼; the flat U₀, and U₁, U₂, U₃, U₄ and U₅. Although not visible in the image, U_n(1) = n + 1 and U_n(−1) = (n + 1)(−1)ⁿ.

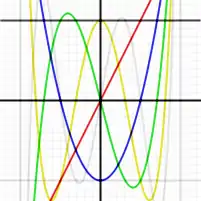
نوع دوم آن هم با همان معادله ی 6 ولی با مقادیر اولیه متفاوت 7 بدست می آیند.

${\displaystyle U_{0}(x)=1,U_{1}(x)=2x(7)}$

${\displaystyle U_{n+1}(x)=2xU_{n}(x)-U{n-1}(x)}$

اولین چندجمله‌ای‌های نوع دوم چبیشف به صورت زیر می‌باشند:

${\displaystyle U_{0}(x)=1\,}$

${\displaystyle U_{1}(x)=2x\,}$

${\displaystyle U_{2}(x)=4x^{2}-1\,}$

${\displaystyle U_{3}(x)=8x^{3}-4x\,}$

${\displaystyle U_{4}(x)=16x^{4}-12x^{2}+1\,}$

${\displaystyle U_{5}(x)=32x^{5}-32x^{3}+6x\,}$

${\displaystyle U_{6}(x)=64x^{6}-80x^{4}+24x^{2}-1\,}$

${\displaystyle U_{7}(x)=128x^{7}-192x^{5}+80x^{3}-8x\,}$

${\displaystyle U_{8}(x)=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1\,}$

${\displaystyle U_{9}(x)=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10x.\,}$

از دیدگاه معادلات دیفرانسیل

چندجمله ای های چبیشف از نگاهی دیگر جوابهای معادله دیفرانسیل زیر هستند

${\displaystyle (1-x^{2})y''-xy'+(\alpha )^{2}y=0}$

که جواب آن به صورت سری توانی زیر خواهد بود و به ازای α های مختلف این چندجمله ای ها به وجود می آیند. ابتدا مشتق های اول و دوم جواب را به دست می آوریم:

${\displaystyle y=\sum _{n=0}^{\infty }a_{n}x^{n}}$

${\displaystyle y'=\sum _{n=0}^{\infty }na_{n}x^{n-1}}$

${\displaystyle =\sum _{i=1}^{\infty }na_{n}x^{n-1}}$

${\displaystyle =\sum _{n=0}^{\infty }(n+1)a_{n+1}x^{n}}$

${\displaystyle y''=\sum _{n=0}^{\infty }(n+1)na_{n+1}x^{n-1}}$

${\displaystyle =\sum _{n=1}^{\infty }(n+1)na_{n+1}x^{n-1}}$

${\displaystyle =\sum _{n=0}^{\infty }(n+2)(n+1)a_{n+2}x^{n}}$

سپس آنها را در معادله اولیه جایگذاری می کنیم:

${\displaystyle (1-x^{2})\sum _{n=0}^{\infty }(n+2)(n+1)a_{n+2}x^{n}-x\sum _{n=0}^{\infty }(n+1)a_{n+1}x^{n}+\alpha ^{2}\sum _{n=0}^{\infty }a_{n}x^{n}=0n}$

${\displaystyle \sum _{n=0}^{\infty }(n+2)(n+1)a_{n+2}x^{n}-\sum _{n=0}^{\infty }(n+2)(n+1)a_{n+2}x^{n+2}-\sum _{n=0}^{\infty }(n+1)a_{n+1}x^{n+1}+\alpha ^{2}\sum _{n=0}^{\infty }a_{n}x^{n}=0}$

اکنون معادله را به گونه ای می نویسیم که توانهای x یکسان شوند و سپس معادله را حل می کنیم:

${\displaystyle \sum _{n=0}^{\infty }(n+2)(n+1)a_{n+2}x^{n}-\sum _{n=2}^{\infty }(n)(n-1)a_{n}x^{n}-\sum _{n=1}^{\infty }(n)a_{n}x^{n}+\alpha ^{2}\sum _{n=0}^{\infty }a_{n}x^{n}=0}$

${\displaystyle 2.1a_{2}+3.2a_{3}x-1.a_{1}x+\alpha ^{2}a_{0}+\alpha ^{2}a_{1}x}$

${\displaystyle +\sum _{n=2}^{\infty }[(n+2)(n+1)a_{n+2}-(n)(n-1)a_{n}-(n)a_{n}+\alpha ^{2}a_{n}]x^{n}=0}$

${\displaystyle (2a_{2}+\alpha ^{2}a_{0})+[6a_{3}+(\alpha ^{2}-1)a_{1}]x}$

${\displaystyle +\sum _{i=2}^{\infty }[(n+2)(n+1)a_{n+2}+(\alpha ^{2}-n^{2})a_{n}]x^{n}=0}$

برای صادق بودن معادله ی بالا باید تمام ضرایب توانهای x و مقدار ثابت صفر شوند:

${\displaystyle (2a_{2}+\alpha ^{2}a_{0})=0}$

${\displaystyle 6a_{3}+(\alpha ^{2}-1)a_{1}=0}$

${\displaystyle a_{n+2}={\frac {n^{2}-\alpha ^{2}}{(n+1)(n+2)}}a_{n}n=0,1,...}$

رابطه ی بازگشتی برای جملات زوج به صورت زیر:

${\displaystyle a_{2}={\frac {-\alpha ^{2}}{2}}a_{0}}$

${\displaystyle a_{4}={\frac {2^{2}-\alpha ^{2}}{3.4}}a_{2}={\frac {(2^{2}-\alpha ^{2})(-\alpha ^{2})}{1.2.3.4}}a_{0}}$

${\displaystyle a_{2n}={\frac {[(2n)^{2}-\alpha ^{2}][(2n-2)^{2}-\alpha ^{2}]...(-\alpha ^{2})}{(2n)!}}a_{0}}$

و برای جملات فرد به صورت زیر خواهد بود:

${\displaystyle a_{3}={\frac {1-\alpha ^{2}}{6}}a_{1}}$

${\displaystyle a_{5}={\frac {3^{2}-\alpha ^{2}}{4.5}}a_{3}={\frac {(3^{2}-\alpha ^{2})(1-\alpha ^{2})}{5!}}a_{1}}$

${\displaystyle a_{2n-1}={\frac {[(2n-1)^{2}-\alpha ^{2}][(2n-3)^{2}-\alpha ^{2}]...(1-\alpha ^{2})}{(2n+1)!}}a_{1}}$

در نهایت جواب عمومی به دست می آید:

${\displaystyle a_{keven}=\prod _{j=1}^{\frac {k}{2}}(k-2j)^{2}-\alpha ^{2}}$

${\displaystyle a_{kodd}=\prod _{j=1}^{\frac {k-1}{2}}(k-2j)^{2}-\alpha ^{2}}$

${\displaystyle y=a_{0}[1+\sum _{k=2,4,...}^{\infty }{\frac {a_{keven}}{k!}}x^{k}]+a_{1}[x+\sum _{k=3,5,...}^{\infty }{\frac {a_{kodd}}{k!}}x^{k}]}$

که می توان به صورت زیر نوشت:

${\displaystyle y=a_{0}cos(\alpha arcsinx)+{\frac {a_{1}}{\alpha }}sin(\alpha arcsinx)}$

و با یک تغییر متغیر به این نتیجه می رسیم:

${\displaystyle y=b_{1}cos(\alpha arccosx)+b_{2}sin(\alpha arccosx)=b_{1}T_{\alpha }(x)+b_{2}{\sqrt {1-x^{2}}}U_{\alpha -1}(x)}$

که (Tn(x چندجمله‌ای چبیشف از نوع اول و (Un(x چندجمله‌ای چبیشف از نوع دوم است.

جستارهای وابسته

• روش‌های طیفی چبیشف

منابع

• چندجمله‌ای‌های چبیشف

پیوند به بیرون

• چندجمله‌ای‌های نوع اول چبیشف
• kaas.no/work/Blog/Entries/2011/7/5_Talk__On_Multivariate_Chebyshev_Polynomials; _from_group_theory_to_PDE_solvers_files/munthekaas_focm11.pdf چندجمله‌ای‌های نوع اول چبیشف
• چندجمله‌ای‌های نوع اول چبیشف
• چندجمله‌ای‌های نوع اول چبیشف
• چندجمله‌ای‌های نوع اول چبیشف
• چندجمله‌ای‌های نوع اول چبیشف