کران چرنوف

کران‌های چرنوف نام خود را از نام هرمان چرنوف گرفته‌است که کرانی با کاهش نمایی برای محدود کردن توزیع دنباله ای (tail distribution) مجموع تعداد متغیر تصادفی می‌دهد. این نابربری کرانی بهتر نسبت به نامساوی‌های دیگر مانند نابرابری مارکف یا نابرابری چبیشف که بر اساس گشتاورهای مرتبه اول و دوم هستند به دست می‌دهند. اگرچه کران چرنوف لازم دارد که متغیرها مستقل باشند، شرایطی که کران‌های مارکف و چبیشف لازم نیست.

ارتباط بسیار نزدیکی بین این کران و کران هافدینگ (Hoeffding's inequality) و کران برنشتین وجود دارد.

تعریف

زمانی که تابع مولد گشتاور متغیر تصادفی X معلوم باشد، می‌توانیم کرانهای خوبی برای {P{X≤a بدست آوریم.

${\displaystyle P\{X\geq a\}\leq e^{-ta}M(t)\qquad t>0}$

${\displaystyle P\{X\leq a\}\leq e^{ta}M(-t)\qquad t>0}$

چون کران‌های چرنوف برای همه tهای مثبت و منفی برقرار است، می‌توان بهترین کران برای {P{X≥a را با استغاده از مقداری از t که (e^-taM(t را حداقل می‌کند به دست آورد. 'کران‌های چرنوف برای متغیر تصادفی نرمال استاندارد' اگر Z متغیر تصادفی نرمال استاندارد باشد، آنگاه تابع مولد گشتاور آن M(t)=e^t2/2است. پس کران چرنوف برای {P{Z≥a برای هر t>0 به صورت زیر است:

${\displaystyle P\{Z\geq a\}\leq e^{-ta}e^{\frac {t^{2}}{2}}}$

حال مقدار t مثبتی که e^(t2/2)-ta را حداقل می‌کند، مقداری است که (t²/2)-ta را حداقل می‌کند، یعنی t=a است؛ بنابراین برای a>0 داریم:

${\displaystyle P\{Z\geq a\}\leq e^{\frac {-a^{2}}{2}}}$

${\displaystyle P\{Z\leq a\}\leq e^{\frac {-a^{2}}{2}}}$

حال مثالی از کاربرد این کران را نشان می‌دهیم. فرض کنیم X₁, … , X_n متغیرهای تصادفی مستقل با توزیع برنولی باشند، که هر کدام دارای احتمال p > 1/2 باشند، احتمال رخداد همزمان بیش از n/2 متغیر تصادفی ${\displaystyle \{X_{k}=1\}}$ برابر است با

${\displaystyle S=\sum \limits _{i=\lfloor {\frac {n}{2}}\rfloor +1}^{n}{\binom {n}{i}}p^{i}(1-p)^{n-i}.}$

کران چرنوف نشان می‌دهد که رابطهٔ بالا دارای کران پایین زیر است:

${\displaystyle S\geq 1-\mathrm {e} ^{-{\frac {1}{2p}}n\left({p-{\frac {1}{2}}}\right)^{2}}.}$

توجه کنید که برای تعدادی نمونهٔ تصادفی با توزیع برنولی داریم ${\displaystyle \mu =np}$

با استفاده از نتایج کران چرنوف (در ادامه) می‌توان نشان داد که

${\displaystyle P\left[S\leq {\frac {n}{2}}\right]=P\left[S\leq \left(1-\left(1-{\frac {1}{2p}}\right)\right)\mu \right]\leq e^{-{\frac {\mu }{2}}\left(1-{\frac {1}{2p}}\right)^{2}}=e^{-{\frac {1}{2p}}n\left(p-{\frac {1}{2}}\right)^{2}}}$

باید توجه کرد که با توجه به خواسته‌های مسئله می‌توان از فرم‌های مختلفی از کران چرنوف استفاده کرد.

یک مثال جالب

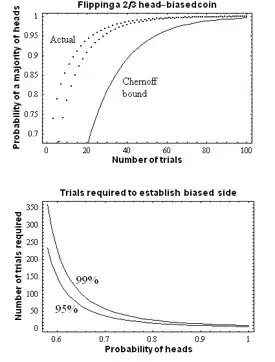
تصور کنید سکه ای اریب داریم (یعنی احتمال رو و پشت با هم یکسان نباشند). اکنون سؤال این است که چطور می‌توان سمتی که دارای احتمال بیشتری است را پیدا؟ جواب ساده این است که سکه را بی نهایب بار پرتاب می‌کنیم و با حساب کردن احتمال هر سمت، آنی که احتمال بیشتری دارد را انتخاب می‌کنیم؛ ولی در عمل چنین کاری انکانپذیر نیست. چگونه می‌توان با تعداد پرتاپ‌های محدود، با احتمالی خوب، حدسی در مورد احتمال سمتی که دارای احتمال رو/پشت بیشتر زد؟

فرض کنیم که ${\displaystyle X_{i}}$ متغیری تصادفی باشد که تعیین می‌کند که آیا پرتاب i-ام رو آمده‌است یا خیر. فرض کنیم بخواهیم مطمئن باشیم که احتمال اینکه سمتی اشتباه را انتخاب کنیم ε باشد. با بازی با رابطهٔ بالا داریم:

${\displaystyle n\geq {\frac {1}{(p-1/2)^{2}}}\ln {\frac {1}{\sqrt {\varepsilon }}}.}$

که حداقل تعداد آزمایش را نشان می‌دهد. به عنوان مثال اگر احتمال موفقیت p = .۶ باشد، اگر بخواهیم با اطمینان ۹۵ درصد، یعنی ${\displaystyle \epsilon =.05}$ قضاوت کنیم، باید حداقل ${\displaystyle (n=150)}$ بار پرتاب انجام دهیم.

یکی از کاربردهای کران چرنوف در بررسی الگوریتم‌های تصادفی (یا در طراحی و بررسی مدل‌های محاسباتی مانند رایانه کوانتومی) برای بررسی حداقل تعداد آزمایش‌های برای رسیدن به درجهٔ مشخصی از اطمینان است.

اثبات نابرابری چرنوف

با استفاده از نابرابری مارکف داریم به ازای هر t > 0:

${\displaystyle \Pr \left[X\geq a\right]=\Pr \left[e^{tX}\geq e^{ta}\right]\leq {\frac {E[e^{tX}]}{e^{ta}}}={\prod _{i}E[e^{tX_{i}}] \over e^{ta}}.}$

با داشتن فرض استقلال بین متغیرها داریم:

${\displaystyle \Pr \left[X\geq a\right]\leq \min _{t>0}{\prod _{i}E[e^{tX_{i}}] \over e^{ta}}.}$

به صورتی مشابه:

${\displaystyle \Pr \left[X\leq a\right]=\Pr \left[e^{-tX}\geq e^{-ta}\right]}$

و

${\displaystyle \Pr \left[X\leq a\right]\leq \min _{t>0}e^{ta}\prod _{i}E[e^{-tX_{i}}].}$

تئوری برای مجموع متغیرهای تصادفی

تئوری ذیل تئوری چرنوف-هافدینگ نام دارد. فرش کنید ${\displaystyle X_{1},X_{2},\ldots ,X_{m}}$ متغیرهای تصادفی مستقل با توزیع یکسان باشند. فرض کنیم ${\displaystyle p=E\left[X_{i}\right]}$, ${\displaystyle X_{i}\in \{0,1\}}$ و ${\displaystyle \varepsilon >0}$. در اینصورت

${\displaystyle {\begin{aligned}&\Pr \left[{\frac {1}{m}}\sum X_{i}\geq p+\varepsilon \right]\\&\qquad \leq \left({\left({\frac {p}{p+\varepsilon }}\right)}^{p+\varepsilon }{\left({\frac {1-p}{1-p-\varepsilon }}\right)}^{1-p-\varepsilon }\right)^{m}=e^{-D(p+\varepsilon \|p)m}\end{aligned}}}$

و

${\displaystyle {\begin{aligned}&\Pr \left[{\frac {1}{m}}\sum X_{i}\leq p-\varepsilon \right]\\&\qquad \leq \left({\left({\frac {p}{p-\varepsilon }}\right)}^{p-\varepsilon }{\left({\frac {1-p}{1-p+\varepsilon }}\right)}^{1-p+\varepsilon }\right)^{m}=e^{-D(p-\varepsilon \|p)m},\end{aligned}}}$

که در آن

${\displaystyle D(x||y)=x\log {\frac {x}{y}}+(1-x)\log {\frac {1-x}{1-y}}}$

دیورژانس کالبک-لیبلر بین متغیرهای تصادفی ${\displaystyle x}$ و ${\displaystyle y}$ است. در صورتی که ${\displaystyle p\geq 1/2}$ در اینصورت

${\displaystyle \Pr \left[X>mp+x\right]\leq \exp(-x^{2}/2mp(1-p)).}$

تئوری برای حالت‌های خاص

در حالت‌های خاص می‌توان از تقارن متغیرها در مسئله استفاده کرد و کران بهتری بدست آورد.

جستارهای وابسته

• نابرابری مارکف
• نابرابری چبیشف

منابع

• مبانی احتمال، نویسنده: شلدون راس، مترجم دکتر احمد پارسیان و علی همدانی، ویرایش هشتم، فصل ۸، بخش ۵.

• Chernoff، H. (۱۹۵۲). «A Measure of Asymptotic Efficiency for Tests of a Hypothesis Based on the sum of Observations». Annals of Mathematical Statistics. ۲۳ (۴): ۴۹۳&ndash, ۵۰۷. doi:10.1214/aoms/1177729330. MR 0057518. Zbl 0048.11804. جی‌استور ۲۲۳۶۵۷۶.
• Hoeffding، W. (۱۹۶۳). «Probability Inequalities for Sums of Bounded Random Variables». Journal of the American Statistical Association. ۵۸ (۳۰۱): ۱۳–۳۰. doi:10.2307/2282952. جی‌استور ۲۲۸۲۹۵۲.
• Chernoff، H. (۱۹۸۱). «A Note on an Inequality Involving the Normal Distribution». Annals of Probability. ۹ (۳): ۵۳۳. doi:10.1214/aop/1176994428. MR 0614640. Zbl 0457.60014. جی‌استور ۲۲۴۳۵۴۱.
• Hagerup، T. (۱۹۹۰). «A guided tour of Chernoff bounds». Information Processing Letters. ۳۳ (۶): ۳۰۵. doi:10.1016/0020-0190(90)90214-I.
• Ahlswede، R.؛ Winter، A. (۲۰۰۳). «Strong Converse for Identification via Quantum Channels». IEEE Transactions on Information Theory. ۴۸ (۳): ۵۶۹–۵۷۹. arXiv:quant-ph/0012127.
• Mitzenmacher، M.؛ Upfal، E. (۲۰۰۵). Probability and Computing: Randomized Algorithms and Probabilistic Analysis. شابک ۹۷۸-۰-۵۲۱-۸۳۵۴۰-۴.
• Nielsen, F. (2011). "Chernoff information of exponential families". arXiv:1102.2684 [cs.IT].
• Sinclair، Alistair. «Class notes for the course "Randomness and Computation" given Fall 2011» (PDF). بایگانی‌شده از اصلی (PDF) در ۳۱ اکتبر ۲۰۱۴. دریافت‌شده در ۲۶ دسامبر ۲۰۱۲.