گراف دوگان

در رشتهٔ ریاضی، گراف دوگان گراف G گرافی است که در هر ناحیه از گراف G یک راس دارد. بین دو راس در گراف دوگان یال وجود دارد، هرگاه دوناحیه از گراف G با یک یال از یکدیگر جدا شده باشند؛ بنابراین، متناظر با هر یال e ازگراف G یالی درگراف دوگان وجود دارد که نواحی طرفین یال e را به هم وصل می‌کند.

نمودار قرمز رنگ گراف دوگان نمودار ابی رنگ است

گراف دوگان یک تعمیم توپولوژیک مفاهیم هندسی چندوجهی‌ها و موزائیک کاری‌های دوبعدی است.

در گراف دوگان واژهٔ "دوگان" از آن جهت مورد استفاده قرار می‌گیرد که گراف دوگان بودن یک رابطهٔ متقارن و دوطرفه است یعنی اگر گراف G گراف دوگان H باشد گراف H نیز گراف دوگان G خواهد بود. هنگامی که در مورد گراف دوگان گراف G بحث می‌شود گراف G ممکن است یک گراف اولیه " primal graph" باشد.

بسته به نوع و خواص گراف G گراف دوگان آن متفاوت است. گراف‌های چند وجهی و دوبعدی گراف دوگان یکتایی دارند درحالی که بعضی گراف‌ها گراف دوگان یکتایی ندارند.

نمونه
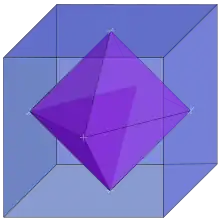
مکعب و هشت وجهی منتظم گراف دوگان دارند.

چند وجهی دوگان

دوگانگی گراف‌های مسطح با مفهوم یک جسم چندوجهی دوگان بسیار مرتبط است. برای یک جسم چندوجهی سه بعدی، گراف این چندوجهی (مجموعه رئوس و یال‌ها) دوگان گراف آن چندوجهی دوگان است. به این علت گراف‌های اجسام افلاطونی به صورت جفت‌های دوگان می‌آیند. گراف K2,2،2 از یک ۸ وجهی منتظم، دوگان گراف مکعب است و غیره. ۴ وجهی منتظم خوددوگان است، بنابراین گراف آن یک K4 نیز هست.

گراف‌های خود دوگان
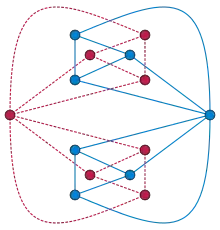
یک گراف خود دوگان. این گراف یک همبند سه یاله است اما یک همبند سه گره‌ای نیست.

یک گراف مسطح را خود دوگان گویند، اگر با گراف دوگان خود یک ریخت باشد. گراف‌های چرخ مجموعه‌ای نامحدود از گراف‌های خود دوگان پدیدمی‌آورند که از چندوجهی‌های خود دوگان (هرم‌ها) پدید می‌آیند. با این حال، گراف‌های خود دوگانی وجود دارند که چندوجهی نیستند، همانند گرافی که نمایش داده شده. Servatius و Christopher دو عملگر توصیف کردند، اتصال و افتراق، که می‌توانند برای ساخت یک گراف دوگان که یک گراف مسطح داده شده‌ای در بردارد به کار رود؛ به‌طور مثال، گراف خود دوگان نشان داده شده می‌توانند به عنوان adhesion از یک چهاروجهی با دوگانش ساخته شود.

با توجه با توجه به فرمول اویلر، هر گراف خود دوگان با n گره، دقیقاً 2n – ۲ یال دارد. هر گراف خود دوگان محاط شده حداقل ۴ وجه مثلثی دارد.

تغییرات

گراف‌های دوگان جهت دار

در یک گراف جهت دار گراف دوگان ممکن است به خوبی جهت دار شود به طوری که با چرخش هر یک از یال‌های گراف دوگان به اندازهٔ ۹۰ درجه در جهت ساعتگرد باعث شود که آن یال بر یال گراف اولیه منطبق شود. صرف سخن باید گفت که این حرکت (ساختن گراف جهت دار با استفاده از چرخش۹۰ درجه) یک رابطهٔ متقارن نیست یعنی اگر گراف G را دو بار به اندازهٔ ۹۰ درجه در راستای ساعت گرد بچرخانیم خودش تشکیل نمی‌شود، بلکه اگر این عمل را ۴ بار روی گراف G تکرار کنیم باعث می‌شود خودش تشکیل شود.

دوگان ضعیف

دوگان ضعیف یک گراف مسطح، زیرگراف گراف دوگانی است که گره‌های آن با وجه‌های محدود گراف اولیه مطابقت می‌کند. یک گراف مسطح، مسطح بیرونی است، اگر و تنها اگر دوگان ضعیف آن جنگل باشد و یک گراف مسطح یک Halin graphاست اگر و تنها اگر دوگان ضعیف آن گراف دوهمبند و مسطح بیرونی باشد. برا ی هر گراف مسطح G، G+را گراف چندگانه مسطحی در نظر بگیرید که با اضافه کردن یک گره تنهای جدید v در بیکران، و مرتبط کردن v به هر گره از وجه بیرونی (چند بار، اگر یک گره چند بار در مرز وجه بیرونی ظاهر شود) آنگاه G یک دوگان ضعیف دوگان (مسطح) G+ است.[1][2]

گراف‌ها بی‌نهایت و موزائیک کاری

همچنین به این نکته باید توجه داشت که فضای خارج گراف G نیز یک ناحیه محسوب می‌شود پس باید یک راس را هم درفضای خارج گراف G در نظر گرفت و اگر بین ناحیهٔ داخلی G و ناحیهٔ خارجی یالی وجود داشته باشد بین راسی که مربوط به ناحیهٔ داخلی است و راسی که درناحیهٔ خارجی قرار دارد یالی ایجاد می‌شود.

پانویس
  1. Fleischner, Herbert J.; Geller, D. P.; Harary, Frank (1974), "Outerplanar graphs and weak duals", Journal of the Indian Mathematical Society, 38: 215–219, MR 0389672.
  2. Sysło, Maciej M.; Proskurowski, Andrzej (1983), "On Halin graphs", Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics, 1018, Springer-Verlag, pp. 248–256, doi:10.1007/BFb0071635.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.