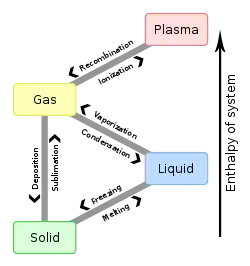
ابرشارگی
ابرشارگی (به انگلیسی: Superfluidity) یک فاز است که غالباً در دماهای پایین دیده میشود، بهطور مثال هلیوم-۳ و هلیوم-۴ دارای یک اصطکاک سطحی میباشند که بعد از گذر از نقطه لاندا، گرانروی این مایع به صفر تبدیل میشود و مایع بدون اصطکاک میتواند جریان یابد.[1] این پدیده ابتدا برای هلیوم مایع کشف شد، اما در اخترفیزیک، انرژیهای بالا و نظریههای گرانش کوانتومی هم دیده میشود. ابرشارگی، نخستین بار برای هلیوم-۴ توسط پیوتر کاپیتسا،[2] جان اف آلن و دن میسنر[3] در سال ۱۹۳۷ کشف شد.

ابر شاره نوعی از ماده است که در آن حالت مانند سیالی که دارای ویسکوزیته و آنتروپی صفر است رفتار میکند. معمولاً هیدروژن، هلیم -۳ و هلیم -۴ در یک حالت که به عنوان نقطه لاندا میگویند، دارای ویسکوزیته صفر میشوند. همانطور که ابر رساناها در برابر جریان هیچ مقاومتی از خود نشان نمیدهند، ابر سیالات نیز بدون هیچ گونه اصطکاکی و بهطور آزادانه میتوانند جریان پیدا کنند. ابر سیالات دارای ویسکوزیته و آنتروپی صفر و رسانایی گرمایی بینهایت میباشند (در نتیجه غیرممکن است که در ابر سیالات گرادیان دما ایجاد کرد همانطور که نمیتوان در ابر رساناها اختلاف ولتاژ ایجاد نمود). یکی از نتایج دیدنی ین خواص که اثر چشمه نامیده میشود، این است که اگر یک لوله مویین را در یک حمام ابر شاره هلیم قرار دهیم و گرما دهیم (حتی با تاباندن نور بر آن) هلیم شروع به بالا آمدن از لوله مویین خواهد کرد (طبق معادله کلازیوس - کلاپیرون). دومین اثر غیرعادی این است که ابر شاره هلیم میتواند فیلمی از شاره به ضخامت یک اتم تشکیل دهد و از اطراف ظرف محتوی آن بالا آید.
این پدیده به چگالش بوز-انیشتین مربوط است ولی با هم یکسان نیستند؛ نه همه ابرشارهها چگالش بوز-انیشتین و نه همهٔ چگالشهای بوز-انیشتین ابرشاره در نظر گرفته میشوند. ابرشارگی در هلیم - ۴ در دماهای بسیار بالاتر از هلیم - ۳ رخ میدهد هر اتم از He-4 یک ذره بوزون، با اسپین صفر است. یک اتم هلیوم-۳ یک ذره فرمیونیک(fermion) است که میتواند بوزون را تنها با جفت شدن با خود را در دماهای بسیار پایینتر تشکیل دهد. این فرایند شبیه به جفت شدن الکترون در ابررسانایی است.
ابرشارگی یک گاز فرمیونی فوق سرد به صورت تجربی توسط Wolfgang Ketterle به اثبات رسید و تیم او گردابهای کوانتومی را در دمای ۵۰ نانوکلوین در MIT در ماه آوریل سال ۲۰۰۵ مشاهده کردند. این چنین گردابهایی قبلاً در یک گاز بوزونی فوق سرد در سال ۲۰۰۰ مشاهده شده بود ولی برای نخستین بار در گازهای دو بعدی دیده میشد.
این ایده که ابرشارگی در داخل ستاره نوترونی وجود دارد اولین بار توسط Arkady Migdal ارائه شدهاست. با بررسی الکترونهای درون زوج قیدهایی که ابر رسانا را به خاطر عکسالعمل بین الکترون و شبکه به وجود میآورند، انتظار میرود که نوکلیونهای درون یک ستاره نوترونی وقتی چگالی به اندازه کافی بالا و دما کم باشد نیز زوج قیدها را به خاطر نیروی اتمی بلند برد به وجود میآورد و موجب ابرسیالی و ابر رسانایی میشود.
ابر شاره هلیوم- ۴

در سال ۱۹۵۰ Hall و Vinen آزمایشهایی انجام دادند که خطوط گردابی تدریجی در ابر شاره هلیم -۴ به وجود آورد،[4] در سال ۱۹۶۰ Rayfield و Reif موفق به ایجاد حلقههای گردابی تدریجی شدند پاکارد تا تقاطع خطوط گرداب با سطح آزاد شاره مشاهده میشود Avenel و Varoquaux اثر جوزفسون در ابرشاره هلیوم -۴ را مورد مطالعه قرار دادند. در سال ۲۰۰۶ یک گروه در دانشگاه مریلند گرداب تدریجی با استفاده از ذرات ردیاب کوچک هیدروژن جامد را تجسم کردند.
ویژگیها
شکل ۱ نمودار فازی هلیم- ۴ است.[5] این نمودار نمودار p بر حسب T که رژیم مایع و جامد با کمک منحنی ذوب از هم جدا شدهاند (بین حالت جامد و مایع) و ناحیه گاز و مایع به کمک خط فشار بخار از هم جدا شدهاند. دومی در نقطه بحرانی به پایان میرسد که در آن نقطه تفاوت بین گاز و مایع از بین میرود. این نمودار نشان میدهد که این ویژگی که هلیم - ۴ حتی در صفر مطلق به حالت مایع است قابل توجهاست، هلیم-۴ جامد فقط در فشار بالاتر از ۲۵ بار جامد است. شکل همچنین خط λ را نشان میدهد. این خطی است که دو رژیم شاره هلیم ۱ و هلیم ۲ را در نمودار فازی از هم جدا میکند. در ناحیهٔ یک هلیم رفتار یک شاره معمولی را دارا میباشد در حالی که در ناحیه دو هلیم یک ابر شاره میباشد.
در زیر خط λ مایع به دو نوع میتواند تشریح شود این رفتارها از دو جزء تشکیل میشود:
۱- یک جز عادی رفتار میکند
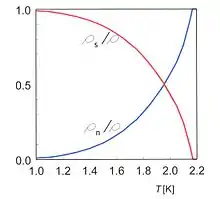
۲- یک جز مثل ابر شاره رفتار میکند با ویسکوزیته و آنتروپی صفر نسبت چگالی مربوط ρn/ρ وρs/ρ, با (ρn (ρs چگالی شاره نرمال (ابر سیال) و ρ (چگالی کلی) به دما وابستهاست و این وابستگی در شکل ۳ نمایش داده شدهاست.[6] با کاهش دما، درصد چگالی ابر شاره از صفر در Tλ به یک در صفر کلوین میرسد. زیر ۱ کلوین هلیم کاملاً به صورت ابرشاره است.
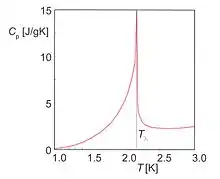
نمودار ۲- تغییرات ظرفیت گرمایی هلیم ۴ با دما را نشان میدهد این شکل ظرفیت گرمایی He-4 مایع در فشار بخار اشباع به عنوان تابعی از دما است. نقطهٔ اوج در T = 2.17 K نشان دهنده انتقال فاز است.
همچنین نام خط λ از رسم دما بر حسب گرما که شکل حرف یونانی λ را درست میکند حاصل شدهاست.[7][8]
جریان فیلمی
بسیاری از مایعات معمولی مثل الکل یا بنزین به خاطر تنش سطحی شان، از دیوارههای جامد به بالا میخزند. هلیوم مایع نیز این ویژگی را دارد، اما در این مورد He-II که به صورت لایهای از مایع اصلی خارج میشود محدود نبودنش در این امر به خاطر ویسکوزیته جریانش نیست بلکه به خاطر سرعت بحرانی اش که حدود cm/s ۲۰ است، میباشد. این سرعت زیاد است در نتیجه ابرشاره هلیوم میتواند به آسانی به بالای دیواره ظرف برود و به پایین و به سطح مایع برگردد. در یک ظرف قطراتی که قابل دیدن هستند به وجود میآیند.
ابر شاره هیدرودینامیک
معادله حرکت ماده ابرشاره به همراه یکسری فرضیات سادهکننده[9] توسط قانون نیوتن تفسیر میشود.
M۴ حجم مولار هلیوم و سرعت ماده ابر شاره است. به مشتق بر حسب زمان مشتق هیدرودینامیک نیز گفته میشود، یعنی نرخ زیاد شدن سرعت هنگام حرکت سیال. در مورد ابر سیالها هلیوم در میدان نیروی جاذبه نیرو با معادله زیر بیان میشود:[10][11]
در این معادله μ پتانسیل شیمیایی مولی، g شتاب جاذبه و z مختصات عمودی است؛ بنابراین حاصل میشود:
این معادله فقط وقتی بر قرار است که vs زیر یک مقدار بحرانی که معمولاً توسط شعاع شاره جریان یافته تعیین میشود، باشد.[12][13] در مکانیک کلاسیک، نیرو معمولاً گرادیان انرژی پتانسیل میباشد. معادله ۱ نشان میدهد که در مورد مواد ابرشاره معادله نیرو عبارتی شامل گرادیان پتانسیل شیمیایی دارد. دلیل ویژگیهای خاص He-II این مورد است.
فشار چشمه
فرمولی که معمولاً ما استفاده میکنیم اینگونهاست:
که در اینجا Smآنتروپی مولی
و Vmحجم مولی است. با معادله بالا (μ(p,Tتوسط یک انتگرال خطی در صفحه P-T محاسبه میشود. اول از مبدأ انتگرال میگیریم تا (p,0) در نتیجه در T =۰. سپس از (p,0) تا (P,T) که فشار ثابت است انتگرال میگیریم. در انتگرال اول dT=۰ و در دومی dp=۰ میباشد. حاصل اینگونه میشود:
در مورد کار ما فشار بسیار کوچک است در نتیجهVm به صورت جرئی ثابت است. در نتیجه:
که در اینجا Vm0 حجم مولار مایع در دما و فشار صفر است. قسمت دیگر معادله ۳ به عنوان محصول Vmنیز نوشته میشود و مقدارpfکه مقدار فشار را دارد.
فشارpf به عنوان فشار چشمه شناخته میشود و توسط آنتروپی هلیوم که توسط ظرفیت گرمایی محاسبه میشود میتوان آن را حساب کرد. اگر T =Tf فشار چشمه برابر bar 0.692 خواهد بود. با توجه به مقدار دانسیته هلیوم مایع (kg/m3 125) و g = 9.8 m/s2 ستونی از هلیوم مایع با ارتفاع ۵۶ متر خواهیم داشت. در نتیجه در آزمایشهای زیادی، فشار چشمه بیشترین اثر را بر حرکت ابر شاره در مقابل جاذبه خواهد داشت.
از معادله ۳ و ۴ و ۵ خواهیم داشت:
معادله ۷ نشان میدهد که ماده ابر شاره با داشتن گرادیان فشار و میدان جاذبه شتاب میگیرد و علاوه بر آن با فشار چشمه نیز این اتفاق میافتد. معادله ۵ فقط از نظر ریاضی معنادار است اما در شرایط آزمایشگاهی خاص pf میتواند مانند فشار واقعی عمل کند. شکل زیر دو لوله را که هردو He-II دارند را نشان میدهد. لوله سمت چپ در دمای صفر کلوین و فشار صفر قرار دارد. لولهها توسط یک superleak متصل شدهاست. اما ماده ابر شاره میتواند درون این superleak بدون هیچ مشکلی (زیر سرعت بحرانی) جریان داشته باشد. در حالت پایدارvs=۰ نتیجه معادله ۷ به صورت زیر میشود:
در اینجا رابطهای که وجود دارد به این گونهاست:
این یعنی که فشار در لوله راستی برابر با فشار چشمهاست در Tr.
در یک آزمایش که مانند شکل ۵ تنظیم شدهاست، یک چشمه را میتوان تولید کرد. اثر چشمه جهت به محاسبه چرخه هلیوم در یک یخچال رقیق ساز استفاده میشود.
انتقال حرارت
شکل ذیل یک آزمایش رسانش را بین دو دمای TH و TL نشان میدهد که توسط یک لولهای که با He-II پر شدهاست، وصل شدهاست. وقتی که به انتهای گرم گرما داده میشود در آنجا یک فشاری مطابق معادله ۷ درست میشود. این فشار جزء عادی را از انتهای گرم به انتهای سرد میبرد مطابق معادله زیر:
در اینجا ηn ویسکوزیته ماده عادی و Z فاکتوری هندسی و حجم جریان است. جریان عادی توسط یک ابر شاره که از انتهای سرد به گرم میرود، متعادل میشود. در قسمت انتهایی یک تبدیل عادی به ابر شاره اتفاق میافتد و برعکس؛ بنابراین گرما توسط نه رسانش بلکه با همرفت منتقل میشود. این نوع انتقال دما بسیار مؤثر است بنابراین رسانش گرمایی این ماده خیلی بهتر از بهترین مواد است. شرایط قابل مقایسه با لولههای حرارتی که حرارت توسط تبدیل گاز به مایع انتقال مییابد. هدایت حرارتی بالایHe-IIبرای تثبیت آهنرباهای ابررسانا استفاده میشود. مانند همانهایی که در CERN استفاده میشود.
ویژگیهای ابرشارهها
- ابرشارهها کیفیت منحصر به فردی دارند از آنجا که تمام اتم هایشان در شرایط کوانتومی یکسانی هستند. این به این معنا است که همگی گشتاور یکسانی دارند و اگر یکی تکان بخورد همگی تکان میخورند. این ویژگی اجازه میدهد به ابر شاره که بدون اصطکاک در کوچکترین ترکها حرکت کند و ابر شاره هلیوم حتی میتواند از اطراف یک ظرف به سمت بالا حرکت کند. این رفتار کاملاً مخالف جاذبه از سطح موج ویژهای که در ابر شاره هلیوم وجود دارد میآید که خروجی اش حرکت فیلمی بسیار نازک از دیواره ظرف است.
- ابرسیالها هدایت حرارتی بهطور شگفتآور زیادی دارند. وقتی به یک سیستم معمولی گرما داده میشود به آرامی در سیستم نفوذ میکند. در یک ابر شاره گرما بسیار سریع انتقال مییابد بهطوریکه وجود موجهای حرارتی ممکن میگردد. این نوع چهارم موجها که در ابر سیالها پیدا میشود به غلط صدای دوم نامیده میشود چون هیچ تغییر فشاری را شامل نمیشود.
با وجود این ویژگیهای عجیب موجی، این موجهای ابر سیالها میتوانند در فشار معمولی نیز انتشار یابند. دانشمندان با این اتفاق عجیب در مقابل موارد عادی بهت زده شدند در نتیجه از یک سیستم دو سیاله استفاده کردند تا ابر سیالها را بررسی کنند. لاندا و تیسزا تئوری ای ارائه دادند با این فرض که ابر شاره از یک درصدی از اتمهای با شرایط و رفتار کوانتومی یکسان دارد که قسمتی از ابر شاره را تشکیل میدهند و درصدی از اتمهای در حالت عادی که متغیر حالت کوانتومی هستند. وقتی به صفر مطلق میرسد مقدار اتمهای عادی کم میشود. این تئوری به زیبایی بیشتر ابر سیالها را توضیح داد اما فیزیکدانان همواره در تلاش برای اضافه کردن به این تئوری هستند از آنجایی که هر روز ویژگیهای جدید کشف میشود.
- پدیده غیرعادی دیگر در مورد ابر سیالها توانایی آنها در فرمولی کردن گردابها است. اگر یک سطل پر از آب را بچرخانید شکلی شبیه گرداب به وجود میآید که آب در مرکز آن با سرعت کمی حرکت میکند و هرچه از مرکز خارج شویم سرعت بیشتر میشود. در یک ابر شاره گردابهای لحظهای به وجود میآید. تعداد گردابها با عدد h/m متناسب است. گردابهای فرموله شده موضوع جالبی برای مطالعه در زمینه سیالهای کوانتومی است و به نظر میرسند از نظر تئوری شبیه خطهای فلاکس در ابر رساناها است.
کاربردها
ابرشارهها میتوانند یک کلاس جدید از حسگرهای فوقالعاده حساس به چرخش برای استفاده در سیستم هدایت دقت و برنامههای کاربردی دیگر ایجاد کنند.
جستارهای وابسته
- ابردیامغناطیس
- چگالش بوز-انیشتین
- ابررسانایی
- Quantum vortex
- ابرجامد
- فیلم ابرشاره
- داگلاس دین اشرفت
- گاهشمار فیزیک دمای پایین
- صدای دوم
یادداشت
- مجله دانشمند شماره آذر ۱۳۸۷ مقاله نظریه ریسمان
- Kapitza, P. (1938). "Viscosity of Liquid Helium Below the λ-Point". Nature. 141 (3558): 74. Bibcode:1938Natur.141...74K. doi:10.1038/141074a0.
- Allen, J. F.; Misener, A. D. (1938). "Flow of Liquid Helium II". Nature. 142 (3597): 643. Bibcode:1938Natur.142..643A. doi:10.1038/142643a0.
- Hall, H. E.; Vinen, W. F. (1956). "The Rotation of Liquid Helium II. II. The Theory of Mutual Friction in Uniformly Rotating Helium II". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. ۲۳۸ (۱۲۱۳): ۲۱۵. Bibcode:1956RSPSA.238..215H. doi:10.1098/rspa.1956.0215.
- Swenson, C. (1950). "The Liquid-Solid Transformation in Helium near Absolute Zero". Physical Review. ۷۹ (۴): ۶۲۶. Bibcode:1950PhRv...79..626S. doi:10.1103/PhysRev.79.626.
- E.L. Andronikashvili Zh. Éksp. Teor. Fiz, Vol.16 p.780 (1946), Vol.18 p. 424 (1948)
- Keesom, W.H.; Keesom, A.P. (1935). "New measurements on the specific heat of liquid helium". Physica. ۲: ۵۵۷. Bibcode:1935Phy.....2..557K. doi:10.1016/S0031-8914(35)90128-8.
- Buckingham, M.J.; Fairbank, W.M. (1961). "The nature of the λ-transition in liquid helium". Progress in Low Temperature Physics. ۳: ۸۰. doi:10.1016/S0079-6417(08)60134-1. ISBN 9780444533098.
|chapter=ignored (help) - S.J. Putterman, Superfluid Hydrodynamics (North-Holland Publishing Company, Amsterdam, 1974) ISBN 0-444-10681-2
- L.D. Landau, J. Phys. USSR, Vol.5 (1941) p.71.
- I.M. Khalatnikov, An introduction to the theory of superfluidity (W.A. Benjamin, Inc. , New York, 1965) ISBN 0-7382-0300-9.
- Van Alphen, W.M.; Van Haasteren, G.J.; De Bruyn Ouboter, R.; Taconis, K.W. (1966). "The dependence of the critical velocity of the superfluid on channel diameter and film thickness". Physics Letters. ۲۰ (۵): ۴۷۴. Bibcode:1966PhL....20..474V. doi:10.1016/0031-9163(66)90958-9.
- De Waele, A.Th.A.M.; Kuerten, J.G.M. (1992). "Thermodynamics and hydrodynamics of ۳He-۴He mixtures". Progress in Low Temperature Physics. ۱۳: ۱۶۷. doi:10.1016/S0079-6417(08)60052-9. ISBN 9780444891099.
|chapter=ignored (help)
منابع
- London, F. Superfluids (Wiley, New York, 1950)
- D.R. Tilley and J. Tilley, ``Superfluidity and Superconductivity, (IOP Publishing Ltd. , Bristol, 1990)
- هاگن کلاینرت، Gauge Fields in Condensed Matter, Vol. I, "SUPERFLOW AND VORTEX LINES", pp. 1–742, World Scientific (Singapore, 1989); Paperback ISBN 9971-5-0210-0 (also available online here)
پیوند به بیرون
- Video including superfluid helium's strange behavior در یوتیوب
- Superfluid phases of helium
- Lancaster University, Ultra Low Temperature Physics - Superfluid helium-3 research group.
- https://web.archive.org/web/20060313075351/http://www.aip.org/png/html/helium3.htm
- https://web.archive.org/web/20060408121158/http://www.aip.org/pt/vol-54/iss-2/p31.html
- http://web.mit.edu/newsoffice/2005/matter.html
- http://physicsweb.org/articles/world/11/6/3/1