الگوریتم ایجاد هزارتو
الگوریتمهای ایجاد هزارتو روشهایی خودکار برای تولید هزارتو (ماز) هستند.
روشهای مبتنی بر نظریه گرافها
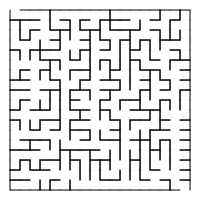
یک هزارتو میتواند توسط یک چیدمان از پیش تعیین شده از خانهها با دیوارهایی در بین آنها تولید شود. خانهها بهطور معمول شبکههای مستطیلی هستند اما چیدمانهای دیگر هم ممکن است. این چیدمانهای از پیش تعیین شده را میتوان در قالب گراف همبند تصور کرد که در آن یالها نشانگر مکانهای ممکن برای دیوار و گرهها نشانگر خانهها باشند. در این صورت هدف این الگوریتم را میتوان ساختن یک زیر گراف در نظر گرفت. زیرگرافی که در آن یافتن یک مسیر بین دو راس مشخص مورد بررسی باشد. اگر زیرگراف همبند نباشد، آنگاه قسمتهایی در گراف وجود خواهد داشت که بیاستفاده میمانند. چرا که آنها نقشی در فضای جستجو بازی نمیکنند. اگر گراف شامل حلقه باشد، آنگاه امکان وجود چندین مسیر بین دو راس مشخص وجود دارد. به همین علت، تولید هزارتو بهطور معمول از طریق تولید درخت پوشای تصادفی انجام میشود. حلقهها میتوانند موجب سردرگمی بازیکنان کمتجربه شوند. حلقهها را میتوان با اضافه کردن یالهای تصادفی به نتیجه در مسیر تولید گراف ایجاد کرد.
جستجوی عمق-اول
این الگوریتم یک نسخه تصادفی از الگوریتم جستجوی عمق-اول است. این الگوریتم که غالباً توسط پشته پیادهسازی میشود یکی از سادهترین راهها برای تولید یک هزارتو توسط رایانه است. فضای هزارتو را یک شبکه بزرگ از خانهها (مانند یک صفحه شطرنج) تصور کنید بهطوریکه هر خانه در آن با ۴ دیوار در اطراف آن وجود دارند. با آغاز از یک خانه تصادفی، برنامه یکی از همسایههای آن خانه را که تاکنون انتخاب نشدهاست بهطور تصادفی انتخاب میکند. حال دیوار بین آن دو خانه برداشته میشود و خانه جدید به پشته اضافه میشود (این کار مشابه کشیدن یک خط روی زمین است). سپس برنامه با همین روند ادامه پیدا میکند، با رسیدن به خانهای که هیچ همسایهٔ قابل عزیمتی ندارد (همه همسایههای آن دیده شدهاند) برنامه به بنبست میرسد. در این مرحله مسیر طی شده در جهت عکس طی میشود تا اولین رأس با حداقل یک همسایه رویت نشده یافت شود. سپس مسیر با رویت این خانه جدید ادامه پیدا میکند (این کار معادل ساخت یک نقطه اتصال در هزارتو است). کار تا جایی ادامه پیدا میکند که تمامی خانهها یکبار رویت شوند. در این حالت برنامه تمام مسیر را به سمت خانه اولیه بازمیگردد. این رویکرد، مشاهده تمام خانههای فضای هزارتو را تضمین میکند. همانطور که پیشتر بیان شد الگوریتم بسیار ساده عمل کرده و به تبع آن هزارتوهای بسیار پیچیدهای را هم تولید نمیکند. برخی اصلاحات مانند اصلاحات زیر میتواند به پیچیدهتر کردن هزارتوهای ساخته شده کمک کند.
- از یک راس مشخص شروع کن و نام آن را خروج بگذار.
- راس کنونی را به عنوان رویت شده علامتگذاری کن و فهرستی از همسایههایش را بگیر. برای هر همسایه و با شروع از یک همسایه تصادفی، اگر آن همسایه هنوز رویت نشده بود، دیوار بین آن و خانه اولیه را حذف کن و سپس برای آن همسایه همین عمل را بهطور بازگشتی انجام بده.
همانطور که در بالا اشاره شد این الگوریتم دربردارنده یک روند بازگشتی عمیق است که در برخی معماریهای رایانه میتواند موجب سرریز از پشته شود. میتوان با ذخیره کردن اطلاعات حاصل از بازگشت از هر خانه بر روی هزارتو الگوریتم را به یک حلقه تغییر داد. این کار در عین حال یک راه سریع برای نشاندادن جواب را نیز ارائه میدهد:
با شروع از هر خانه و بازگشت مسیر به سمت خانه خروج میتوان مسیر موردنظر را تولید کرد.
هزارتوهایی که با روش جستجوی عمق-اول ایجاد میشوند ضریب شاخه کمتری دارند (شکستهای کمتری در هر شاخه به وجود میآورند) و راهروهای زیادی را دربردارند. این امر باعث میشود که الگوریتم جستجوی عمق-اول برای تولید هزارتو در بازیهای ویدئویی مناسب باشد. با حذف کردن تصادفی تعدادی از دیوارها در هزارتوی تولید شده با این روش، میتوان راهروهای طولانی و باریک را شاخهدارتر کرد. این روش برای تولید هزارتوهایی با درجه دشواری کمتر مناسب است. همچنین این حالت نیز برای تولید بازیهای ویدئویی مطلوب است.
پسگردان بازگشتی
الگوریتم جستجوی عمق-اول در تولید هزارتو بهطور معمول با استفاده از روش پسگرد Backtrack پیادهسازی میشود.
- خانه اول را خانه جاری قرار بده و آن را به عنوان دیدهشده علامت بزن.
- تا زمانی که خانهای وجود دارد که دیده نشده باشد:
- اگر خانه جاری همسایهای دارد که دیده نشدهاست:
- یکی از همسایهها را بهطور تصادفی انتخاب کن.
- خانه جاری را در داخل پشته قرار بده.
- دیوار بین خانه جاری و خانه انتخاب شده را حذف کن.
- خانه انتخاب شده را خانه جاری قرار بده و آن را به عنوان دیده شده علامت بزن.
- در غیر این صورت اگر پشته خالی نبود:
- یک خانه را از سر پشته بردار.
- آن را خانه جاری قرار بده.
- در غیر این صورت:
- یک خانه تصادفی را انتخاب کن و آن را خانه جاری قرار بده و آن را به عنوان دیدهشده علامت بزن.
- اگر خانه جاری همسایهای دارد که دیده نشدهاست:
الگوریتم تصادفی کروسکال
این الگوریتم نسخه تصادفی الگوریتم کروسکال است.
- فهرستی از تمامی دیوارها تهیه کن و یک مجموعه برای هر خانه ایجاد کن که تنها عضو آن همان خانه باشد.
- برای هر دیوار با یک ترتیب تصادفی کارهای زیر را انجام بده:
- اگر خانههایی که با این دیوار از یکدیگر جدا میشوند به مجموعههای متفاوتی تعلق داشتند:
- دیوار جاری را حذف کن.
- این مجموعهها را با یکدیگر ادغام کن.
- اگر خانههایی که با این دیوار از یکدیگر جدا میشوند به مجموعههای متفاوتی تعلق داشتند:
داده ساختارهای متفاوتی وجود دارند که میتوانند مجموعههایی از خانهها را شبیهسازی کنند. یک راه پیادهسازی کارا که توسط داده ساختار مجموعههای مجزا صورت میگیرد، میتواند هر عمل اجتماع و یافتن روی دو مجموعه را بهطور سرشکن در زمان خطی انجام دهد (بهطور دقیق تر زمان ; به ازای هر ).
بنابراین زمان اجرای این الگوریتم در اصل با تعداد دیوارهای موجود در هزارتو متناسب است.
این مسئله که فهرست دیوارها ابتدا بهطور تصادفی مقداردهی اولیه شود یا هر دیوار بهطور تصادفی از بین فهرست غیرتصادفی از دیوارها انتخاب شود، اهمیت چندانی ندارد. هر کدام از این دو روش نیز در پیادهسازی در یک سطح از سادگی قرار دارند.
از آنجا که نتیجه این الگوریتم، تولید درخت پوشای کمینه یک گراف با یالهای هموزن است، الگوریتم به سمت تولید الگوهای منظمی که به نسبت سادهتر حل میشوند، متمایل است.
الگوریتم تصادفی پریم
این الگوریتم نسخه تصادفی الگوریتم پریم است.
- با یک شبکه پر از دیوارها شروع کن.
- یک خانه را انتخاب کن، آن را به عنوان یک بخش از هزارتو علامت بزن. دیوارهای اطراف آن خانه را به فهرست دیوارها اضافه کن.
- تا زمانی که فهرست دیوارها عضو دارد:
- یک دیوار را بهطور تصادفی انتخاب کن، اگر خانه در سمت دیگر دیوار هنوز به هزارتو اضافه نشدهاست:
- دیوار را یک گذرگاه قرار بده و خانهای که در سمت دیگر دیوار قرار داشت را بخشی از هزارتو قرار بده.
- دیوارهای همسایه این خانه را در فهرست دیوارها قرار بده.
- اگر خانه در سمت دیگر دیوار قبلاً به هزارتو اضافه شده بود، دیوار مورد بررسی را از فهرست دیوارها حذف کن.
- یک دیوار را بهطور تصادفی انتخاب کن، اگر خانه در سمت دیگر دیوار هنوز به هزارتو اضافه نشدهاست:
مانند الگوریتم جستجوی عمق-اول، یافتن راه به سمت خانه اول معمولاً به نسبت ساده است اما به سمت دیگر خانههای هزارتو دشوار.
توجه کنید که اجرای الگوریتم کلاسیک پریم بر روی یک گراف با وزن تصادفی هزارتوهایی با الگویی مشابه با هزارتوهای تولید شده در الگوریتم کروسکال ایجاد میکند. چرا که هر دو الگوریتم به یافتن درخت پوشای کمینه اختصاص دارند. در عوض، الگوریتم حاضر الگوی متفاوتی از هزارتوها را ایجاد میکند. چرا که یالهای نزدیکتر به نقطه آغازین وزن مؤثر کمتری دارند.
نسخه اصلاح شده
با وجود اینکه الگوریتم کلاسیک پریم فهرستی از یالها را ذخیره میکند، برای تولید هزارتو میتوان لیستی از خانههای مجاور به هر خانه را ذخیره کرد. اگر یک خانه تصادفی توسط چندین یال به هزارتو موجود متصل شود یکی از این یالها بهطور تصادفی انتخاب میشود. این روش تمایل بیشتری به ایجاد شاخه نسبت به روش بالا که مبتنی بر ذخیره یال بود دارد.
روش تقسیم بازگشتی
هزارتوها میتوانند از طریق تقسیمات بازگشتی ساخته شوند. یک الگوریتم برای این کار در زیر شرح داده شدهاست:
از یک فضای بدون دیوار شروع کن و آن را یک اتاق بنام. اتاق را با دیوارهایی که بهطور تصادفی قرار میگیرند تقسیم کن (برای هر دیوار یک دهانه برای شروع یک راهرو، در نقطهای تصادفی روی آن دیوار قرار دارد). حال بهطور بازگشتی همین عملیات را روی اتاقهای درونی انجام بده تا زمانی که همه اتاقها به اندازه کمینه برسند. این روش منجر به تولید هزارتوهایی میشود که در آنها دیوارهای راست و طولانی عبور میکنند. این الگو هزارتوهایی تولید میکند که در آنها نواحیای که بهتر است از ورود به آنها خودداری شود، سادهتر دیده میشوند.
برای مثال، در یک هزارتو مستطیلی، در یک نقطه تصادفی از فضا دو دیوار که به یکدیگر عمود هستند را بسازید. این دو دیوار اتاق اولیه را به چهار اتاق کوچکتر تقسیم میکنند که توسط چهار دیوار از یکدیگر جدا شدهاند. سه دیوار از این چهار دیوار را بهطور تصادفی انتخاب کنید و یک روی هر کدام از آنها و در نقطهای تصادفی بر روی آنها یک دهانه ورودی به عرض یک واحد ایجاد کنید.
این روند را بهطور بازگشتی ادامه دهید تا زمانی که تمامی اتاقها عرضی برابر یک واحد در یکی از بعدهای خود داشته باشند.
الگوریتمهای ساده
الگوریتمهای دیگری نیز وجود دارند که تنها به میزان کافی حافظه برای ذخیره یک ردیف از یک هزارتو دوبعدی یا یک صفحه از یک هزارتو سهبعدی نیازمند هستند. این الگوریتمها با ذخیره کردن خانههایی در ردیف کنونی که به خانههایی از ردیف قبل مسیر دارند، از ایجاد حلقه جلوگیری میکنند.
اکثر الگوریتمهای تولید هزارتو برای اطمینان از قابل حل بودن هزارتو نهایی، نیازمند نگهداری ارتباط میان خانههای درونی هستند. هرچند هزارتوهای معتبر و همبند تنها با تمرکز بر روی هر خانه قابل تولید هستند.
هزارتو درخت دودویی، یک هزارتو استاندارد با خطوط عمود بر هم است که در آن هر خانه یک راهرو به سمت بالا یا چپ دارد اما هر دو آنها را نمیتواند داشته باشد.
برای ساخت یک هزارتو درخت دودویی، برای هر خانه با انداختن سکه تصمیم گرفته میشود که حرکت به سمت بالا یا چپ انجام شود. برای خانههای روی مرز همواره یک جهت اتخاذ میشود و نتیجه نهایی یک هزارتو معتبر همبند ساده خواهد بود که ظاهری مانند درخت دودوییای دارد که ریشه آن، خانه بالا سمت چپ است.
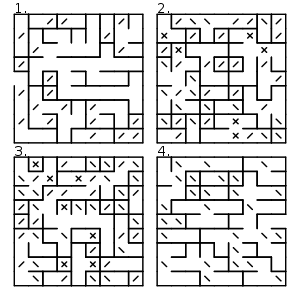
جایگزین انداختن سکه برای هر خانه، ساخت یک عکس با استفاده از ترکیبی تصادفی از کاراکترهای ممیز و ممیز رو به عقب ("\") است. این روش یک هزارتو همبند ساده و معتبر را ایجاد نمیکند اما گروهی از حلقههای بسته را ایجاد میکند (راهنمای استفاده از کمودور ۶۴ یک برنامه پایه را با استفاده از این الگوریتم ارائه میدهد، با این تفاوت که از کاراکترهای مورب گرافیکی PETSCII برای یک نمایش گرافیکی روانتر استفاده میکند).
الگوریتمهای خودکاره مشبک
انواع مشخصی از خودکارههای شبکه میتوانند در تولید هزارتو مورد استفاده قرار گیرند[1]. دو نوع مشهور از این خودکارههای شبکه، ماز و مازکتریک، دارای قوانین رشتهایB۳/S۱۲۳۴۵ و B۳/S۱۲۳۴ هستند[1].
در حالت اول، این بدان معنی است که هر خانه به این شرط از یک مرحله به مرحله بعدی باقی میماند که حداقل یک و حداکثر پنج همسایه داشته باشد. در حالت دوم، هر خانه با داشتن یک تا چهار همسایه باقی میماند. اگر خانهای دقیقاً سه همسایه داشته باشد متولد میشود.
برای یک الگوی شروع تصادفی، این خودکارههای تولیدکننده هزارتو مشبک به تولید هزارتوهایی پیچیده منجر میشوند که دیوارهای راهروهای آن بهطور غیرمبهمی ترسیم شدهاند.
مازکتریک که دارای قانون B۳/S۱۲۳۴ است، در مقایسه با ماز با قانون B۳/S۱۲۳۴۵ گرایشی به تولید راهروهای طولانی و باریک دارد[1]. این یک عیب قابل توجه محسوب میشود چرا که این هزارتوها به نسبت قابل پیشبینی میشوند.
مانند برخی از روشهای مبتنی بر نظریه گراف که در بالا به تفصیل بیان شد، این خودکارههای مشبک عموماً هزارتوهایی از یک الگوی آغازین یکتا تولید میکنند؛ بنابراین معمولاً منجر به تولید هزارتوهایی میشوند که یافتن راه به خانه ابتدایی در آنها به نسبت ساده است، حال آنکه راهیابی به دیگر خانهها به نسبت دشوارتر است.
شبه کد جاوا
class MazeBuilder implements Runnable {
public static final int CW_TOP = 1;
public static final int CW_BOT = 2;
public static final int CW_LEFT = 4;
public static final int CW_RIGHT = 8;
static final int CW_VIRGIN = 16;
public static final int CW_ALL = CW_TOP|CW_BOT|CW_LEFT|CW_RIGHT;
static final int CW_BOUND_SHIFT = 5;
static final int CW_TOP_BOUND = 32;
static final int CW_BOT_BOUND = 64;
static final int CW_LEFT_BOUND = 128;
static final int CW_RIGHT_BOUND = 256;
static final int CW_ALL_BOUNDS =
CW_TOP_BOUND|CW_BOT_BOUND|CW_LEFT_BOUND|CW_RIGHT_BOUND;
static final int CW_IN_ROOM = 512;
public static int dirsx[] = { 1, 0, -1, 0 };
public static int dirsy[] = { 0, 1, 0, -1 };
int width, height, startx, starty;
int cells[][], origdirs[][], dists[][];
boolean can_go(int x, int y, int dx, int dy) {
int bit = get_bit(dx, dy) << CW_BOUND_SHIFT;
if ((cells[x][y] & bit) != 0)
return false;
return (cells[x+dx][y+dy] & CW_VIRGIN) != 0;
}
int get_bit(int dx, int dy) {
int bit = 0;
switch (dx + dy * 2) {
case 1: bit = CW_RIGHT; break;
case -1: bit = CW_LEFT; break;
case 2: bit = CW_BOT; break;
case -2: bit = CW_TOP; break;
default: dbg("get_bit problem "+dx+" "+dy); break;
}
return bit;
}
Random random;
Maze maze;
int randno(int lo, int hi) {
return (Math.abs(random.nextInt()) % (hi-lo+1)) + lo;
}
void delwall(int x, int y, int dx, int dy) {
int bit;
bit = get_bit(dx, dy);
cells[x][y] &= ~bit;
bit = get_bit(-dx, -dy);
cells[x+dx][y+dy] &= ~bit;
}
void delbound(int x, int y, int dx, int dy) {
int bit;
bit = get_bit(dx, dy);
cells[x][y] &= ~(bit << CW_BOUND_SHIFT);
bit = get_bit(-dx, -dy);
cells[x+dx][y+dy] &= ~(bit << CW_BOUND_SHIFT);
}
void addboundwall(int x, int y, int dx, int dy) {
int bit = get_bit(dx, dy);
cells[x][y] |= bit | (bit<<CW_BOUND_SHIFT);
int bit2 = get_bit(-dx, -dy);
cells[x+dx][y+dy] |= bit2 | (bit2<<CW_BOUND_SHIFT);
}
int partiters = 0;
int grade_partition(Vector sl, Seg pe) {
int x = pe.x;
int y = pe.y;
int dx = pe.dx;
int dy = pe.dy;
int lcount = 0, rcount = 0, splits = 0;
int inc = 1;
if (sl.size() >= 100)
inc = sl.size() / 50;
for (int i = 0; i < sl.size(); i += inc) {
Seg se = (Seg) sl.elementAt(i);
int df1x = se.x-x;
int df1y = se.y-y;
int sendx = se.x + se.dx;
int sendy = se.y + se.dy;
int df2x = sendx - x;
int df2y = sendy - y;
int nx = dy;
int ny = -dx;
int dot1 = df1x * nx + df1y * ny;
int dot2 = df2x * nx + df2y * ny;
if (getSign(dot1) != getSign(dot2)) {
if (dot1 == 0)
dot1 = dot2;
else if (dot2 != 0) {
splits++;
continue;
}
}
if (dot1 > 0 ||
(dot1 == 0 && se.GetDir() == pe.GetDir())) {
rcount++;
} else if (dot1 < 0 ||
(dot1 == 0 && se.GetDir() == -pe.GetDir())) {
lcount++;
} else {
dbg("grade_partition problem: dot1 = "+dot1+", dot2 = "+dot2);
}
}
return Math.abs(lcount-rcount) + splits * 3;
}
Vector seglist;
static int getSign(int num) {
return (num < 0) ? -1 : (num > 0) ? 1 : 0;
}
void Initialize() {
int x, y;
for (x = 0; x != width; x++) {
for (y = 0; y != height; y++) {
cells[x][y] = CW_VIRGIN | CW_ALL;
}
cells[x][0] |= CW_TOP_BOUND;
cells[x][height-1] |= CW_BOT_BOUND;
}
for (y = 0; y != height; y++) {
cells[0][y] |= CW_LEFT_BOUND;
cells[width-1][y] |= CW_RIGHT_BOUND;
}
}
void Generate() {
int x, y;
y = 0;
int firstx = x = randno(0, width-1);
int dir = 0;
int origdir = dir;
cells[x][y] &= ~CW_VIRGIN;
while (true) {
int dx = dirsx[dir], dy = dirsy[dir];
if (!can_go(x, y, dx, dy)) {
dir = (dir+1) & 3;
if (origdir == dir) {
if (x == firstx && y == 0)
break;
int odr = origdirs[x][y];
dx = dirsx[odr];
dy = dirsy[odr];
x -= dx;
y -= dy;
origdir = dir = randno(0, 3);
}
} else {
delwall(x, y, dx, dy);
x += dx;
y += dy;
cells[x][y] &= ~CW_VIRGIN;
origdirs[x][y] = dir;
origdir = dir = randno(0, 3);
}
}
جستارهای وابسته
منابع
- Nathaniel Johnston; et al. (21 August 2010). "Maze - LifeWiki". LifeWiki. Retrieved 1 March 2011.
پیوند به بیرون
- Jamis Buck: HTML 5 Presentation with Demos of Maze generation Algorithms
- Think Labyrinth: Maze algorithms (details on these and other maze generation algorithms)
- Maze Generation - Master's Thesis (Java Applet enabling users to have a maze created using various algorithms and human solving of mazes)
- http://rosettacode.org/wiki/Maze Collection of maze generation code] in different languages in Rosetta Code]
- Maze generation and navigation in 3D