الگوریتم تارژان مؤلفههای قویا همبند
الگوریتم تارژان (نامگذاری: مبدع، رابرت تارژان)، از الگوریتمهای تئوری گراف است که برای پیدا کردن مؤلفههای قویاً همبند در یک گراف استفاده میشود. با وجود اینکه، این الگوریتم از نظر زمانی مقدم بودهاست، میتوان دید که نسخهٔ بهبود یافته الگوریتم کساراجو و از نظر کارایی (بازده) با الگوریتم مؤلفه قوی مبتنی بر مسیر قابل مقایسه است.
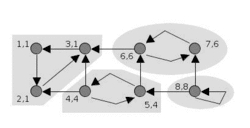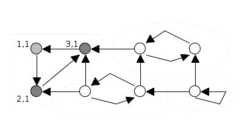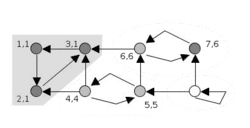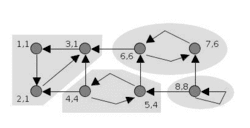 تجسم الگوریتم تارژان مؤلفههای قویا همبند | |
| ساختمان داده | گراف |
|---|---|
| کارایی بدترین حالت | |
نمای کلی
الگوریتم به عنوان ورودی گراف جهت داری را میگیرد، و افرازی از رئوس گراف به مؤلفههای قویاً همبند تولید میکند. هر راسی (گره) از گراف، دقیقاً یک بار در مؤلفههای همبند ظاهر میشود. هر راس که در یک دور جهت دار نیست، خودش به عنوان یک مؤلفههای قویاً همبند انتخاب میشود: برای مثال، راسی که درجه ورودی و درجه خروجی آن صفر باشد، یا هر راس از گراف بدون دور به تنهایی یک مؤلفهٔ قویاً همبند حساب میشوند. ایدهی ابتدایی این الگوریتم: الگوریتم جستجو عمق اول با راس دلخواه شروع میکند (و جستجوی بعدی عمق اول، بر روی راسهایی اعمال میشود که دیده نشدهاند). با الگوریتم جستجوی عمق اول، جستجو، هر راسی گراف را دقیقاً یک بار میبیند؛ بنابراین، مجموعه ی درخت جستجو، یک جنگل پوشا از گراف است. مؤلفههای قویاً همبند، به عنوان زیردرختهای معین این درخت پوشا، به دست خواهد آمد. ریشهی این زیردرختها را، ریشهی مؤلفههای قویاً همبند میگویند. هر راسی از مؤلفههای قویاً همبند ممکن است به عنوان ریشه به کار گرفته شود، اگر اولین راسی باشد که از آن مؤلفه دیده میشود.
پشته ثابت
راسها به ترتیبی که دیده میشوند در داخل پشته جای میگیرند. زمانی که جستجوی عمق اول به صورت بازگشتی، راسی V و فرزاندانش را ملاقات کند، آن راسها، نباید تا قبل از بازگشت این فراخوانی بازگشتی از پشته، POP شوند. خاصیت یکسانی (ثابت)، این است که، یک راس بعد از پیمایش، بر روی پشته باقی میماند، اگر و تنها اگر مسیری به برخی از راسهای پایینتر در پشه وجود داشته باشد. بعد از اتمام فراخوانی ای که V و فرزاندان آن را پیدا میکند، ما میدانیم که آیا V به هر راسی قبل از خودش در پشته مسیر دارد یا خیر. اگر چنین بود فراخوانی بازمیگردد. V را در پشته به عنوان ثابت، نگاه میدارد. اگر نه، V باید ریشهی مؤلفههای قویاً همبند باشد که شامل V و راسهای بعدی در پشته است. (راسهایی که به V مسیر دارند ولی به ماقبل V مسیری ندارند). تمام مؤلفهها، POP میشود و ثابت را نگه میدارد.
پیادهسازی
هر راسی v به یک عدد صحیح، v.index اختصاص داده میشود که اعداد راسها بصوت متوالی، بترتیبی که پیدا شدهاند، قرار داده میشود. همچنین یک مقدار، v.lowlink که کوچکترین اندیس هر راسی شناخته شدهی قابل دسترس از v، شامل خود v را نمایش میدهد، نگه داشته میشود؛ بنابراین، v باید سمت چپ پشته باشد اگر v.lowlinke <v.index در حالی که، v باید به عنوان ریشه مؤلفه قویاً همبند حذف شود اگر v.lowlink==v.index. مقدار v.lowlink، در حین جستجوی عمق اول از v محاسبه میشود، همانطور که راسهای قابل دسترس از v را پیدا میکند.
شبه کد
algorithm tarjan is input: graph G = (V, E) output: set of strongly connected components (sets of vertices)
index := ۰ S := empty for each v in V do
if (v.index is undefined) then
strongconnect(v) end if end for
function strongconnect(v) // Set the depth index for v to the smallest unused index v.index := index v.lowlink := index index := index + 1 S.push(v)
// Consider successors of v
for each (v, w) in E do
if (w.index is undefined) then
// Successor w has not yet been visited; recurse on it
strongconnect(w)
v.lowlink := min(v.lowlink, w.lowlink)
else if (w is in S) then
// Successor w is in stack S and hence in the current SCC
v.lowlink := min(v.lowlink, w.index)
end if
end for
// If v is a root node, pop the stack and generate an SCC
if (v.lowlink = v.index) then
start a new strongly connected component
repeat
w := S.pop()
add w to current strongly connected component
until (w = v)
output the current strongly connected component
end if
end function
index variable همان شماره راس (گره) در الگوریتم جستجوی اول عمق میباشد. S پشتهٔ راسها میباشد که در ابتدا خالی میباشد و برای ذخیرهسازی راسهایی که دیده شدهاند ولی هنوز به مؤلفههای قویاً همبند ملحق نشدهاند میباشد. ذکر این نکته مهم است که این پشته همان پشتهٔ جستجوی اول عمق نمیباشد در واقع با خروج آن راس در الگوریتم جستجوی اول عمق از پشته حذف نمیشود و تنها در صورتی راسها حذف میشوند که یک مؤلفهٔ قویاً همبند پیدا شود تا تمامی رأسهای آن حذف شود. بیرونیترین حلقه در کد بالا در بین راسهایی که هنوز دیده نشدهاند جستجو میکند تا تضمین کند که راسهایی که از راس اول قابل دسترسی نیستند نیز دیده خواهند شد. تابع strongconnect یک جستجوی اول عمق را انجام میدهد که تمامی فرزندان راس v را میبیند و تمامی مؤلفههای قویاً همبند آن زیر گراف را پیدا میکند. هنگامی که هر راسی تابع بازگشتی جستجوی اول عمقش تمام میشود اگر مقدار lowlink آن برابر اندیس آن باشد یعنی آن راس ریشهٔ یک مؤلفهٔ قویاً همبند شامل تمام راسهای بالاتر از آن درون پشته خواهد بود. الگوریتم تمامی راسهای بالاتر از انرا از پشته خارج میکند و همهٔ آنهارا به عنوان یک مؤلفه در نظر میگیرد.
منابع
- Tarjan, R. E. (1972), "Depth-first search and linear graph algorithms", SIAM Journal on Computing 1 (2): 146–160, doi:10.1137/0201010
- Harrison, Paul. "Robust topological sorting and Tarjan's algorithm in Python". Retrieved 9 February 2011.