الگوریتم مؤلفه قوی مبتنی بر مسیر

الگوریتم مؤلفه قوی مبتنی بر مسیر (به انگلیسی: Path-based strong component algorithm) در نظریه گراف برای پیدا کردن مولفه‌های قویا همبند یک گراف جهت‌دار استفاده می‌شود. قبل از این الگوریتم، الگوریتم کساراجو و الگوریتم تارژان نیز به همین منظور ارائه شده‌است.

مفاهیم
  • گراف قویا همبند

به گراف جهت‌داری گویند که هر جفت راس آن از یکدیگر قابل دسترس باشد. مانند شکل زیر:

گراف قویا همبند
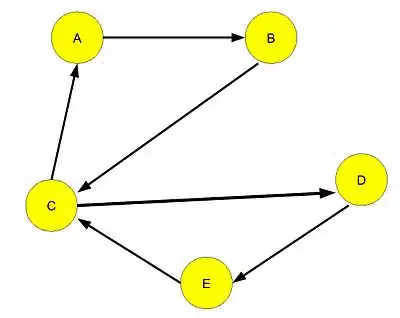
  • مؤلفه قویا همبند:

مولفه قویا همبند یک گراف به بیشینه زیرمجموعه‌ای از رأس‌ها گویند که قویا همبند هستند. یعنی از هر جفت راس در آن مجموعه به یکدیگر مسیر مستقیم وجود دارد. مانند شکل زیر:

مولفه‌های قویا همبند

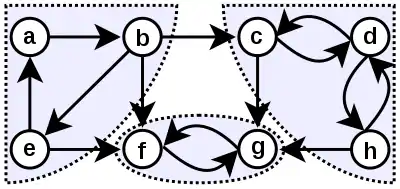
الگوریتم

فرض کنید گراف G داده شده‌است. در این الگوریتم رأس‌های گراف را از ۱ تا n و مؤلفه‌های قویا همبند را با شروع از n+۱ شماره‌گذاری می‌کنیم. همچنین در این الگوریتم گراف H را که در ابتدا همان گراف G می‌باشد در نظر می‌گیریم و در این گراف مسیر P را به صورت زیر می‌سازیم: ابتدا یک رأس دلخواه از گراف را در نظر می‌گیریم و از این رأس در جهت کاملاً دلخواه حرکت می‌کنیم تا یکی از دو حالت زیر رخ دهد:

  • اگر به رأسی رسیدیم که قبلاً در مسیر P وجود داشت، تمام گره‌های بین این رأس که تاکنون پیموده شده‌است را هم در گراف H و هم در مسیر p منقبض می‌کنیم. یعنی همه آن‌ها را به عنوان یک رأس در نظر می‌گیریم.
  • اگر به رأسی رسیدیم که دیگر نتوانستیم مسیر P را ادامه دهیم، گره آخر مسیر P را هم در گراف H وهم در مسیر P حذف کرده و آن را به عنوان یک مؤلفه قویا همبند معرفی می‌کنیم.

این الگوریتم از الگوریتم جستجوی عمق اول و همچنین دو پشته برای نمایش مسیر P استفاده می‌کند. پشته S که شامل دنباله رأس‌های مسیر P است و پشته B که شامل کران‌های رأس‌های منقبض شده‌است. در این الگوریتم آرایه I نیز وجود دارد که هم اندیس پشته S را و هم شماره مؤلفه قویا همبند را ذخیره می‌کند. به عبارت دقیق تر این ارائه به صورت زیر تعریف می‌شود:

  • I[v]=۰ هرگاه گره v در مسیر P نباشد.
  • I[v]=j هرگاه گره v اکنون در مسیر P باشد و S[j]=v.
  • I[v]=c هرگاه مؤلفه قویا همبند شامل v حذف شده و با عدد c شماره گذاری شده باشد.

این الگوریتم شامل قسمت اصلی STRONG و قسمت بازگشتی DFS است:

AlgorithmSTRONG(G)
۱ empty stacks S and B
۲ for v ∈ V do I[v]=۰
۳ c=n
۴ for v ∈ V do if I[v]=۰ then DFS(v)
AlgorithmDFS(G)
۱ PUSH(v,S);I[v]=TOP(S);PUSH(I[v],B);/*add v to the end of P*/
۲ for edges (v,w) ∈ E do
۳   if I[w]=۰ then DFS(w)
۴   else /*contract if necessary*/
۵      while I[w]<B[TOP(B)] do POP(B)
۶ if  I[v]=B[TOP(B) then{/*number vertices of the next strong component*/
۷    POP(B);increase c by 1
۸    while I[v]≤TOP(S) do I[POP(S)]=c}

در قضیه زیر برهان درستی و همچنین پیچیدگی این الگوریتم آمده‌است:

قضیه

هنگامی که (STRONG(G متوقف شود هر رأس v ∈ V به مؤلفه قویا همبندی که توسط [I[v شماره گذاری شده‌است تعلق دارد. همچنین زمان و حافظه مصرفی (O(m+n می‌باشند.

برای اثبات قضیه فوق می‌توانید به [۱] مراجعه کنید.

الگوریتم‌های مرتبط

برای دیدن الگوریتم‌های مرتبط با این الگوریتم می‌توانید به الگوریتم کساراجو و الگوریتم مؤلفه‌های همبند قوی تارجان مراجعه کنید.

الگوریتم گابو

الگوریتم چریَن- ملورن/ گابو در نظریه گراف، یک روش با پیچیدگی زمانی خطی برای یافتن مؤلفه‌های همبندی قوی در یک گراف جهتدار است[1] . این الگوریتم در سال ۱۹۹۶ توسط جوزف چِریَن و
کورت ملورن[2] ارائه شد و در سال ۱۹۹۹ توسط هارولد گابو[3] بهبود یافت.
الگوریتم گابو همانند الگوریتم مؤلفه‌های همبند قوی تارجان، تنها یک جستجوی عمق اول در گراف داده شده انجام می‌دهد، و از یک پشته برای نگهداری گره‌هایی که
به مؤلفه‌ای اختصاص داده نشده‌اند استفاده می‌کند، و بعد از اختصاص دادن آخرین گره به مولفه همبندی، این گره‌ها را به یک مؤلفهٔ جدید منتقل می‌کند.
الگوریتم تارجان از یک آرایه با اندیس گره‌ها شامل اعداد پیش‌ترتیب استفاده می‌کند، که به ترتیب دیده شدن در جستجوی عمق اول مقداردهی شده‌اند.
از آرایهٔ پیش‌ترتیبی برای دانستن اینکه چه زمانی مولفهٔ همبندی جدید ایجا شود استفاده می‌گردد. الگوریتم گابو به جای استفاده از آرایه، از پشتهٔ دیگری به این منظور استفاده می‌کند.

الگوریتم گابو با پشتیبانی دو پشتهٔ S و P یک جستجوی عمق اول بر روی گراف داده شدهٔ G انجام می‌دهد. پشتهٔ S تمامی گره‌هایی را تاکنون به یک مؤلفهٔ همبندی قوی
اختصاص داده نشده‌اند، شامل می‌شود. گره‌ها در این پشته به ترتیبی که جستجوی عمق اول به آن می‌رسد قرار دارند. پشتهٔ P شامل گره‌هایی است که هنوز اختصاص آن‌ها به مولفه‌های همبندی
قوی متفاوت از هم، تعیین نشده‌است. همچنین در الگوریتم از یک شمارندهٔ C که تعداد گره‌های مشاهده شده تاکنون است، برای محاسبهٔ اعداد پیش‌ترتیب گره‌ها استفاده می‌شود.

هنگامی که جستجوی عمق اول به یک گره v می‌رسد، الگوریتم مراحل زیر را به ترتیب انجام می‌دهد:

  1. عدد پیش‌ترتیب v را برابر C قرار می‌دهد، و مقدار C را یکی افزایش می‌دهد.
  2. گره v را در پشتهٔ S و همینطور P قرار می‌دهد.
  3. برای هر یال از گره v به گره مجاور w:
    • اگر عدد پیش‌ترتیب w هنوز مقداردهی نشده، به‌طور بازگشتی جستجو را روی w انجام می‌دهد؛
    • در غیر اینصورت، اگر w هنوز به یک مؤلفهٔ همبندی قوی اختصاص داده نشده:
      • تا زمانی که عدد پیش‌ترتیب عنصر بالای پشته P، بزرگتر اکید عدد پیش‌ترتیب w است، عنصر بالای P را خارج می‌کند.
  4. اگر v عنصر بالای P بود:
    • عناصر بالای S را تا زمانی که v خارج شود، خارج کرده و این عناصر را به یک مؤلفهٔ همبندی اختصاص می‌دهد.
    • گره v را از P خارج می‌کند.

الگوریتم کلی شامل یک حلقه روی گره‌های گراف G است، که این جستجوی بازگشتی را برای گره‌هایی که هنوز عدد پیش‌ترتیب آن‌ها مقدار دهی نشده‌است، صدا می‌زند.

منابع
  1. Sedgewick, R., "19٫8 Strong Components in Digraphs", Algorithms in Java, Part 5 – Graph Algorithms year = 2004 (3rd ed.), Cambridge MA: Addison-Wesley, pp. 205–216 line feed character in |title= at position 46 (help)
  2. Cheriyan, J.; Mehlhorn, K. (1996), "Algorithms for dense graphs and networks on the random access computer", Algorithmica, 15: 521–549, doi:10.1007/BF01940880
  3. Gabow, H.N. (2003), "Searching (Ch 10.1)", in Gross, J. L.; Yellen, J., Discrete Math. and its Applications: Handbook of Graph Theory, 25, CRC Press, pp. 953–984

مشارکت‌کنندگان ویکی‌پدیا. «Path-based strong component algorithm». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۹ ژوئن ۲۰۱۳.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.