الگوریتم حذف معکوس

در نظریهٔ گراف الگوریتم حذف معکوس(به انگلیسی: Reverse-delete algorithm) الگوریتمی است که در یک گراف همبند، با یال وزن دار درخت پوشای کمینه را بدست می‌آورد. اگر گراف ناهمبند باشد این الگوریتم درخت پوشای کمینه را برای هر مولفهٔ همبندی می‌یابد که در این صورت مجموعهٔ این درخت‌های پوشای کمینه را یک جنگل پوشای کمینه گویند.

این الگوریتم الگوریتمی حریصانه است که در هر لحظه بهترین انتخاب را انجام می‌دهد و برعکس الگوریتم کروسکال که الگوریتم دیگری برای پیدا کردن درخت پوشای کمینه‌است، عمل می‌کند. الگوریتم کراسکال با یک گراف خالی شروع می‌کند و یال‌ها را به آن اضافه می‌کند در حالیکه الگوریتم حذف معکوس با گراف اصلی شروع می‌کند و یال‌ها را از آن حذف می‌کند. الگوریتم به صورت زیر عمل می‌کند:

  • با گراف G که لیستی از یال‌های E دارد شروع کن.
  • E را به ترتیب نزولی وزن یال‌ها مرتب کن.
  • برای هر یال چک کن که آیا حذف این یال گراف را ناهمبند می‌کند یا نه.
  • اگر حذف کردن منجر به ناهمبندی گراف نمی‌شود یال را حذف کن

اثبات درستی

الگوریتم حذف معکوس این تضمین را می‌دهد که گراف همبند باقی بماند، چون تنها در صورتی یالی را حذف می‌کند که باعث ناهمبند شدن گراف نشود. هر یالی که حذف می‌شود قبل از حذف در دوری شرکت داشته‌است. از آنجایی که الگوریتم از یال با بیشترین وزن شروع به حذف کردن می‌کند، آن یال بزرگ‌ترین یال در دور مربوط به خود است. پس بنابر تعریف درخت پوشای کمینه، یال حذف شده جزء درخت پوشای کمینه نخواهد بود.

شبه برنامه

 
 1  function ReverseDelete(edges[] E)
 2    sort E in decreasing order
 3    Define an index i ← 0
 4    while i <size(E)
 5       Define edge temp ← E[i]
 6	   delete E[i]
 7	   if temp.v1 is not connected to temp.v2
 8             E[i] ← temp
 9   	   i ← i + 1
 10   return edges[] E

در بالا گراف، مجوعه یال‌های وزن دار E است که هر یال آن وزنی دارد و دو راس v1 و v2 را به هم متصل می‌کند.

مثال

در مثال زیر یال‌های سبز توسط الگوریتم انتخاب شده‌اند و یال‌های قرمز حذف شده‌اند.

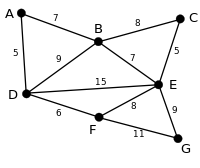این گراف اصلی است. اعداد کنار هر یال وزن هر یال را نشان می‌دهد.
الگوریتم با یال با بیشترین وزن که در اینجا یال DE با وزن ۱۵ است شروع به کار می‌کند. چون حذف یال DE گراف را ناهمبند نمی‌کند الگوریتم این یال را حذف می‌کند.
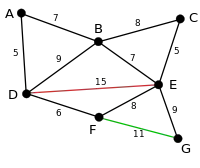بزرگ‌ترین یال بعدی یال FG می‌باشد. الگوریتم چک می‌کند که آیا حذف این یال گراف را ناهمبند خواهد کرد. چون با حذف این یال گراف ناهمبند نمی‌شود این یال هم حذف خواهد شد.
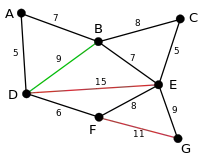بزرگ‌ترین یال بعدی یال BD می‌باشد. الگوریتم یال را چک می‌کند و سپس حذف می‌کند.
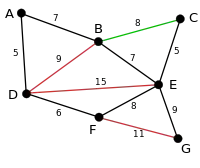یال بعدی که چک می‌شود یال EG است که حذف نخواهد شد چون حذف شدن این یال گراف را ناهمبند خواهد کرد. بنابراین یال بعدی که باید حذف شود یال BC می‌باشد.
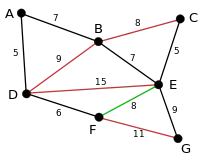بزرگ‌ترین یال بعدی یال EF است که الگوریتم آن را چک می‌کند و حذف می‌کند.
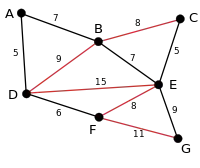الگوریتم باقی گراف را برای یافتن یالی برای حذف کردن می‌گردد اما یالی پیدا نمی‌کند بنابراین این گراف پایانی است که توسط الگوریتم بازگردانده می‌شود.

زمان اجرا

می‌توان نشان داد که الگوریتم در زمان (O(E log E (log log E)3 انجام می‌شود که E تعداد یال‌ها و V تعداد گره‌های گراف است. این حد به صورت زیر محاسبه شده‌است:

مرتب سازی یال‌ها با استفاده از الگوریتم مرتب سازی مقایسه‌ای در زمان (O(E log E انجام می‌گیرد حلقه E بار تکرار می‌شود.

حذف کردن یال در(O(1 زمان انجام می‌گیرد.

همبندی در زمان (O(log V (log log V)3 انجام می‌گیرد.

زمان اجرا را می‌توان (O(E log V (log log V)3 در نظر گرفت زیرا E حداکثر V2 است. یادآوری log V2 = 2 * log V که ثابت ۲ در نوشتار big-O نادیده گرفته می‌شود.[1]

منابع
  1. مشارکت‌کنندگان ویکی‌پدیا. «Reverse-delete algorithm». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۱۱ نوامبر ۲۰۱۰.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.