بازی‌های منصفانه

در نظریه بازی‌های ترکیبیاتی، بازی منصفانه (به انگلیسی: Impartial game) به بازی گفته می‌شود که حرکت‌های قابل قبول تنها به وضعیت بستگی دارد نه به اینکه آخرین بار چه کسی حرکت کرده‌است و درحالی که حاصل متقارن می‌باشد.

در یک بازی منصفانه مستقل از این‌که نوبت کدام بازیکن است، امکانات یکسانی وجود دارد.

بازی‌های منصفانه می‌توانند توسط نظریه سپرگو-گراندی تحلیل شوند.

از جمله این بازی‌ها می‌توان نیم [1]، نیمبل [2]، نیم پکر [3] و دلار نقره‌ای ان.جی.دی براین [4] را نام برد.

بازی که منصفانه نباشند را بازی پارتیزانی می‌نامیم. مانند بازی‌های گو [5]، بازی درافت [6]، شطرنج، تیک-تاک-تو [7]، تخته نرد یا نقطه بازی [8].

نیم

تاریخچه

گفته می‌شود که این بازی در چین ابداع شده‌است و در زمان‌های دور بازی می‌شده‌است. ( نیم شباهت زیادی یه بازی چینی جی‌ان‌شی‌زی Jianshizi دارد) اما چگونگی پیدایش آن نامشخص است؛ اروپاییان نیز در آغاز قرن شانزدهم با نیم آشنا شدند. نام رایج این بازی توسط سی. ال. بوتون (Charles L. Bouton) که تئوری کامل این بازی را در سال 1901 میلادی ایجاد کرد.؛ ابداع شد.

نیم احتمالاً از آلمانی بگیر! (nimm) یا فعل مهجور انگلیسی nim با همین معنا گرفته شده‌است.

قوانین بازی

نیم یک بازی راهبردی (استراتژیک) ریاضی است که با کپه‌هایی از سنگ‌ریزه (یا لوبیا، چوب‌کبریت، چیپس) انجام می‌شود. در هر نوبت هر بازیکن از یک کپه حداقل یک سنگ‌ریزه بر می‌دارد (بازیکن حتی می‌تواند تمام کپه را نیز بردارد). نیم اغلب به این صورت بازی می‌شود که بازیکنی که آخرین سنگ‌ریزه را برمی‌دارد بازنده است. (misere). اما می‌توان به‌طور معمولی نیز بازی کرد به این معنا که بازیکنی که نتواند چیزی را بردارد بازنده است (کسی که آخرین سنگ‌ریزه را برمی‌دارد). این را به این دلیل معمولی گفتیم چون اکثر بازی‌ها چنین رویه‌ای را دنبال می‌کنند.

ما در ادامه نیم معمولی را در نظر می‌گیریم.

مثالی از یک بازی نیم

یک بازی نیم را با کپه‌های {۳، ۴ و ۵} تایی در نظر بگیرید

C	B	A
۵	۴	۳	بازیکن یک ۲ سنگ ریز از A بر می‌دارد.
۵	۴	۱	بازیکن دو ۳ سنگ ریز از C بر می‌دارد.
۲	۴	۱	بازیکن یک ۱ سنگ ریز از B بر می‌دارد.
۲	۳	۱	بازیکن دو ۱ سنگ ریز از B بر می‌دارد.
۲	۲	۱	بازیکن یک ۱ سنگ ریز از A بر می‌دارد.
۲	۲	۰	بازیکن دو ۱ سنگ ریز از B بر می‌دارد.
۲	۱	۰	بازیکن یک ۱ سنگ ریز از C بر می‌دارد. (در misere تمام C را بر می‌داشت وپیروز می‌شد)
۱	۱	۰	بازیکن دو ۱ سنگ ریز از A بر می‌دارد و پیروز می‌شود.
۱	۰	۰	بازیکن یک آخرین سنگ ریز از A بر می‌دارد.

بنابراین وضعیت {۳، ۴، ۵} را یک N-وضعیت می‌گوییم. به‌طورکلی در یک N-وضعیت بازیکن اول می‌تواند با حرکات مناسب حتماً به پیروزی برسد و در یک P-وضعیت بازیکن دوم می‌تواند با حرکات مناسب حتماً به پیروزی برسد.

در بازی با تعداد کپه کم می‌توان به راحتی N-وضعیت‌ها و P-وضعیت‌ها را یافت. برای مثال:

در نیم یک کپه‌ای

n} , n> ۰} یک N-وضعیت است

{۰} یک P-وضعیت است.

در نیم دو کپه‌ای

m, n} , n ≠ m} یک N-وضعیت است

{n, n} یک P-وضعیت است.

برای یک کپه‌ای که علت آن پر واضح است اما برای دو کپه‌ای اگر اندازه دو کپه برابر باشد نفر دوم با تقلید حرکات نفر اول می‌تواند مطمئن باشد که برنده خواهد شد و اگر اندازه دو کپه برابر نباشد نفر اول با برداشتن مقدار اضافی از کپه اول می‌تواند اندازه دو کپه را برابر کند و این بار او با ترفند تقلید به پیروزی برسد.

با افزایش تعداد کپه‌ها بررسی این موضوع پیچیده‌تر می‌شود که به صورت یک مسئله ریاضی آن را حل می‌کنیم

الگوریتم ریاضی

نیم به صورت ریاضی برای تعداد متناهی از کپه‌ها و سنگ‌ریزه‌ها حل شده‌است و می‌توان مشخص نمود که کدام بازیکن برنده خواهد شد.

با جمع دودویی (باینری) اندازه کپه‌ها می‌توان این مسئله را حل نمود. به این ترتیب که معادل دودویی اندازه کپه‌ها را بدون درنظرگرفتن رقم نقلی با هم جمع کرد. این عمل همان یاءانحصاری (XOR) در مدارهای منطقی است که در تئوری بازی‌های ترکیبیاتی (Combinatorial Games) آن را جمع نیمی (nim-sum) می‌نامند. ما برای نشان دادن جمع نیمی از همان نمایش آن در مدارهای منطقی که ${\displaystyle \oplus }$ است؛ استفاده می‌کنیم. جمع نیمی را می‌توان به صورت ذهنی انگشان دست هم حساب نمود. به این ترتیب که انگشتان دست را به ترتیب توان‌های 2 در نظر می‌گیرند و اگر عددی دارای آن توان 2 بود آن را بالا می‌برند و اگر دارای آن توان نبود آن را پایین می‌آورند و در جمع با سایر اعداد اگر آن عدد دارای توانی از 2 بود وضعیت مربوط به آن انگشت را برعکس می‌کنند؛ یعنی اگر بالا بود آن را پایین می‌آورند و اگر پایین بود آن را بالا می‌برند.

در بازی معمولی استراتژی برد صفر کردن جمع نیمی اندازه کپه‌هاست که این امر تا زمانی‌که جمع نیمی آن‌ها 0 نشده‌است ممکن است. اگر جمع نیمی صفر شود بازیکنی که نوبت آن است خواهد باخت. (در صورتی که بازیکن دیگر اشتباه نکند). ما فرض می‌کنیم که در هر نوبت هر بازیکن بهترین حرکت ممکن را انجام می‌دهد. برای آن‌که بدانیم در هر مرحله چه حرکتی باید انجام دهیم؛ جمع نیمی کپه‌ها را X در نظر می‌گیریم. با جمع نیمی اندازه هر کپه با X، کپه‌ای را که اندازه آن کم شده‌است را پیدا می‌کنیم. استراتژی برد در بازی با چنین کپه‌ای است. برای مثال بالا داریم:

${\displaystyle X=3\oplus 4\oplus 5=2}$

${\displaystyle A\oplus X=3\oplus 2=1}$

${\displaystyle B\oplus X=4\oplus 2=6}$

${\displaystyle C\oplus X=5\oplus 2=7}$

تنها کپه‌ای که اندازه آن کاهش یافته A است؛ بنابراین برای برنده شدن در حرکت خود اندازه A را به 1 کاهش می‌دهیم.

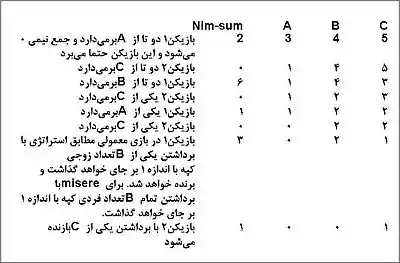
وقتی که به صورت misere بازی می‌کنیم؛ استراتژی بازی فقط در مقایسه با بازی معمولی این تغییر را می‌کند تلاش می‌کنیم که در هر حرکت هیچ کپه‌ای با اندازه بیشتر از 1 بر جای نگذاریم. در این مورد حرکتی درست است که تعداد فردی از کپه‌ها با اندازه 1 بر جای گذارد. در بازی معمولی استراتژی برد در باقی گذاشتن تعداد زوجی از کپه‌ها با انداره 1 است.

در بازی نیم به صورت misere با کپه‌های 3، 4 و 5 استراتژی به صورت زیر است:

اثبات الگوریتم

درستی الگوریتم بالا توسط بوتون اثبات شد..

قضیه : در بازی نیم معمولی نفر اول برنده می‌شود (یک N-وضعیت است) اگر و تنها اگر جمع نیمی اندازه کپه‌ها غیر صفر باشد. در غیر این صورت نفر دوم برنده می‌شود (یک P-وضعیت است).

اثبات : می‌دانیم که جمع نیمی (XOR) از قوانین جابه‌جایی و شرکت‌پذیری پیروی می‌کند. هم‌چنین داریم:

${\displaystyle x\oplus x=0\,\!}$

${\displaystyle x_{1},x_{2},...,x_{n}\,\!}$ را برابر با اندازه کپه‌ها قبل از حرکت و ${\displaystyle y_{1},y_{2},...,y_{n}\,\!}$ را برابر با اندازه کپه‌ها بعد از حرکت قرار می‌دهیم:

${\displaystyle s=x_{1}\oplus x_{2}\oplus ...\oplus x_{n}\,\!}$

${\displaystyle t=y_{1}\oplus y_{2}\oplus ...\oplus y_{n}\,\!}$

اگر سنگ‌ریزه از کپه k-ام برداشته شود خواهیم داشت:

${\displaystyle \forall \;i\neq \;k\Rightarrow \;x_{i}>y_{i}\,\!}$

پس داریم:

${\displaystyle t=0\oplus t\,\!}$

${\displaystyle =s\oplus s\oplus t\,\!}$

${\displaystyle =s\oplus (x_{1}\oplus x_{2}\oplus ...\oplus x_{n})\oplus (y_{1}\oplus y_{2}\oplus ...\oplus y_{n})\,\!}$

${\displaystyle =s\oplus (x_{1}\oplus y_{1})\oplus (x_{2}\oplus y_{2})\oplus ...\oplus (x_{n}\oplus y_{n})\,\!}$

${\displaystyle =s\oplus 0\oplus 0\oplus ...\oplus (x_{k}\oplus y_{k})\oplus ...\oplus 0\,\!}$

${\displaystyle \Rightarrow \;\,\!}$ ${\displaystyle t=s\oplus x_{k}\oplus y_{k}\,\!}$

لم1: اگر ${\displaystyle s=0\,\!}$ باشد آن‌گاه ${\displaystyle t\neq \;0\,\!}$ است و مهم نیست که چه حرکتی انجام شود.

اثبات: اگر انجام هیچ حرکتی ممکن نباشد یعنی کپه‌ها تهی هستند و بازیکن اول بازنده است. در غیراین‌صورت با حرکت در کپه ${\displaystyle k\,\!}$ خواهیم داشت ${\displaystyle t=x_{k}\oplus y_{k}\,\!}$ و این حاصل حتماً غیر صفر است زیرا ${\displaystyle x_{k}\neq \;y_{k}\,\!}$ است.

لم2: اگر ${\displaystyle s\neq \;0\,\!}$ باشد آن‌گاه می‌توان حرکتی انجام داد که ${\displaystyle t=0\,\!}$ شود.

اثبات: ${\displaystyle d\,\!}$ را برابر با سمت چپ‌ترین بیت غیر صفر ${\displaystyle s\,\!}$ در نمایش دودویی قرار می‌دهیم و ${\displaystyle k\,\!}$ را نیز ${\displaystyle d\,\!}$-امین بیت ${\displaystyle x_{k}\,\!}$ که آن‌هم غیر صفر است؛ انتخاب می‌کنیم (${\displaystyle k\,\!}$ حتماً وجود دارد زیرا در غیراین‌صورت ${\displaystyle d\,\!}$-امین بیت ${\displaystyle s\,\!}$ صفر می‌شد). پس ${\displaystyle y_{k}=s\oplus x_{k}\,\!}$ و ما ادعا می‌کنیم که${\displaystyle y_{k}<\;x_{k}\,\!}$ . زیرا همه بیت‌های سمت چپ ${\displaystyle d\,\!}$ مشابه هستند و در ${\displaystyle x_{k}\,\!}$ و ${\displaystyle y_{k}\,\!}$ بیت ${\displaystyle d\,\!}$ از 1 به 0 کاهش می‌یابد.(ارزش آن ${\displaystyle 2^{k}\,\!}$ تا کاهش می‌یابد)، و هر تغییری در بیت‌های باقی‌مانده حداکثر ${\displaystyle 2^{k-1}\,\!}$ تاست. بنابراین بازیکن اول می‌تواند ${\displaystyle x_{k}-y_{k}\,\!}$ تا سنگ‌ریزه از کپه ${\displaystyle k\,\!}$-ام بردارد. در این صورت خواهیم داشت:

${\displaystyle t=s\oplus x_{k}\oplus y_{k}\,\!}$

${\displaystyle \ =s\oplus x_{k}\oplus (s\oplus x_{k})\,\!}$

${\displaystyle \ =0\,\!}$

نیم پکر

قوانین بازی

نیم پکر نیز مانند نیم با کپه‌هایی از سنگ‌ریزه (یا لوبیا، چوب‌کبریت، چیپس) انجام می‌شود. و همانند بازی نیم هر بازیکن می‌توانند اندازه کپه‌ها را با برداشتن تعدادی از سنگ‌ریزه‌ها کاهش دهد؛ اما بازیکنان در این بازی می‌توانند اندازه کپه‌ها را با افزودن سنگ‌ریزه‌هایی که در نوبت‌های قبل بدست آورده‌اند افزایش دهند. این دو حرکت، تنها حرکت‌های مجاز این بازی‌اند.

مثالی از یک بازی نیم پکر

در یک بازی نیم پکر سه کپه با اندازه‌های {3, 4, 5} وجود دارد و بازی مدتی است که شروع شده‌است و هر بازیکن مقدار قابل توحه‌ای سنگ‌ریزه ذخیره کرده‌است؛ اکنون نوبت بازیکن1 است و او بازی را به {1, 4, 5} که وضعیت خوبی در بازی نیم است می‌برد. اما بازیکن2، 50 تا سنگ‌ریزه به کپه با اندازه 4 اضافه می‌کند و وضعیت {1, 54, 5} را ایجاد می‌کند. به نظر می‌رسد که بازی پیچیده شده‌است.

بازیکن1 باید چه بکند؟ بعد از مدتی فکر کردن او فقط 50 تا سنگ‌ریزه‌ای را که ابازیکن2 اضافه کرده بود؛ برمی‌دارد و بازی را به وضعیت قبل در می‌آورد. مهم نیست که بازیکن2 در این بین چقدر سنگ‌ریزه ذخیره کرده‌است یا چند تا سنگ ریزه اضافه می‌کند؛ زیرا هم تعداد سنگ‌ریزه‌هایی که ذخیره کرده‌است متناهی است وهم ما همواره می‌توانیم آن مقداری را که بازیکن2 اضافه کرده‌است برداریم و بازی را مثل بازی نیم معمولی دنبال کنیم.

استراتژی برد

با توجه به مطالب قسمت قبل هر بازیکنی که بتواند در یک وضعیت نیم معمولی برنده شود در نیم پکر با همان وضعیت نیز می‌تواند برنده شود. زیرا اگر بازیکن مقابل اندازه کپه‌ای را کاهش دهد او مطابق با استراتژی بازی نیم پیش می‌رود. و اگر بازیکن مقابل اندازه کپه‌ای را افزایش دهد؛ او حرکت بازیکن مقابل را با برداشتن مقداری که ابه کپه اضافه کرده‌است خنثی می‌کند و بازی را به وضعیت قبل برمی‌گرداند. در این حالت فقط پایان بازی به تأخیر می‌افتد.

Hexapawn

Hexapawn یک بازی دونفره است که توسط مارتین گاردنر (Martin Gardner) ابداع شد. این بازی روی یک مستطیل n×m انجام می‌شود و هر بازیکن m مهره در اختیار دارد که در ردیف اول و آخر در مقابل هم قرار می‌گیرند. برای مثال روی یک صفحه 3×3 .

این بازی برای 3×3 آن حل شده است و اگر هر دو بازیکن خوب بازی کنند حتماً نفر دوم خواهد برد. در این بازی به نظر می‌رسد که هیچ بازیکنی نمی‌تواند تمام مهره‌های حریفش را بزند.

در این بازی مانند شطرنج هر مهره مانند مهره سرباز شطرنج می‌تواند دو نوع حرکت انجام دهد. یک خانه رو به جلو در صورت خالی بودن آن خانه یا زدن مهره حریف به صورت حرکت قطری با اندازه یک. اما در این بازی برخلاف شطرنج در حرکت ابتدایی مهره‌ها نمی‌توانند دو خانه به جلو حرکت کنند.

شطرنج داوسون

توماس رینر داوسون (Thomas Rayner Dawson) سلطان شطرنج منصفانه، یک بازی با دو ردیف سرباز روی یک صفحه شطرنجی n×3 اختراع کرد. قوانین این بازی مانند بازی Hexapawn است با این قانون اضافی که زدن مهره حریف در صورت فراهم شدن موقعیت، اجباری است. فارغ از محتوای شطرنجی آن، این بازی معادل با بازی است که با یک ردیف مهره انجام می‌شود و در آن یک حرکت عبارت است از برداشتن یک مهره همراه با (یک یا دو) مهره مجاورش، در صورت وجود. اگر این بازی را با کپه‌های سنگ‌ریزه به جای ردیف‌هایی از مهره انجام از مهره‌ها انجام دهید؛ قاعده بیان شده را می‌توان به این صورت بیان کرد:

0 کپه، اگر دقیقاً یک سنگ‌ریزه برداشته شود (هیچ مهره مجاوری برداشته نشود)

0 یا 1 کپه، اگر دقیقاً دو سنگ‌ریزه برداشته شود (یک مهره مجاور برداشته شود)

0 یا 1 یا 2 کپه، اگر دقیقاً سه لوبیا برداشته شود (دو مهره مجاورش برداشته شود)

به عنوان مثال، از یک ردیف‌هشتایی، می‌توانید به یک ردیف شش‌تایی، یا به یک ردیف پنج‌تایی، یا به دو ردیف 1 و 4تایی یا 2 و 3تایی برسید. یک مهره یا سنگ‌ریزه خود به تنهایی یک ردیف یا کپه باشد؛ می‌توان برداشت. ریچارد کنت گای (Richard Kenneth Guy) و سدریک اوستون باردل اسمیت این شرایط را به وسیله کد رقمی، برای هر تعداد سنگ‌ریزه 0، 1، 2، ... که ممکن است برداشته شود؛ به صورت رمزی در آوردند. برای شطرنج داوسون رقم‌های رمزی به صورت زیر هستند.

برای برداشتن یک سنگ‌ریزه ${\displaystyle 1=2^{0}\,\!}$

برای برداشتن دو سنگ‌ریزه${\displaystyle 3=2^{1}+2^{0}\,\!}$

برای برداشتن سه سنگ‌ریزه${\displaystyle 7=2^{2}+2^{1}+2^{0}\,\!}$

و بازی شطرنج داوسون برچسب 137• را می‌گیرد؛ که اولین رقم رمز بعد از نقطه، شرایطی است که تحت آن می‌توانید یک سنگ‌ریزه را بردارید؛ رقم دوم شرایطی است برای برداشتن دو سنگ‌ریزه و سومین رقم سرایط برای برداشتن رقم سوم را نشان می‌دهد.

به‌طور کلی، اگر در یک بازی بتوانیم k سنگ‌ریزه از یک کوپه برداریم؛ با این فرض که باقی‌مانده کپه دقیقاً به a کپه ناتهی، یا b کپه، یا c کپه، یا ... (a، b، c و ... متمایزاند) تقسیم شود، به این بازی رمز ${\displaystyle d_{k}=2^{a}+2^{b}+2^{c}+...\,\!}$ را برای برداشتن k سنگ‌ریزه می‌دهیم.

پانویس

1. Nim
2. Nimble
3. Poker Nim
4. N. G. de Bruijn’s Silver Dollar Game
5. Go
6. Checkers
7. دوز
8. Dot game

پیوند به بیرون

• Nim as a web page (javascript) Play against your PC
• Play Nim online
• Poker nim
• Pearls Before Swine
• UVa Problem on Nim
• Nim-Game in Flash
• Ultimate Nim: The Use of Nimbers, Binary Numbers and Subpiles in the Optimal Strategy for Nim
• Mathematical Games
• Hexapawn - an article by Robert Price.
• Hexapawn - on chessvariants.com
• Hexapawn java applet - source code included
• .

منابع

• ریچارد ک. گای (۱۳۸۰)، بازی منصفانه، ترجمهٔ عبادالله محمودیان، آناهیتا آریاچهر، دانشگاه صنعتی شریف، موسسه انتشارات علمی از پارامتر ناشناخته |کشور= صرف‌نظر شد (کمک)
• ژوزف ماکویچ. «Combinatorial Games (Part I): The World of Piles of Stones». انجمن ریاضیات آمریکا. دریافت‌شده در ۳ ژوئیه ۲۰۰۸.
• مشارکت‌کنندگان ویکی‌پدیا. «Nim». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳ ژوئیه ۲۰۰۸.
• مشارکت‌کنندگان ویکی‌پدیا. «Dawson's chess». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳ ژوئیه ۲۰۰۸.
• مشارکت‌کنندگان ویکی‌پدیا. «Impartial game». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳ ژوئیه ۲۰۰۸.

• Elwyn R. Berlekamp, John H. Conway, K. Guy (1982), Winning Ways for your Mathematical Plays, Academic Press, ISBN 0-12-091101-9