برج هانوی

برج هانویْ (در بعضی منابع «برج‌های هانویْ») (به انگلیسی: Tower of Hanoi) از سه میله و تعدادی دیسک در اندازه‌های متفاوت تشکیل شده‌است که می‌توان آن‌ها را بر میله‌ها جای داد.[1][2]

تاریخچه و صورت مسئله

در محوطه معبدی در آسیای دور سه میله الماسی قرار داشت که یکی از آن‌ها حاوی تعدادی قرص طلایی بود. کاهنان معبد در تلاش بودند تا قرص‌های طلایی را از آن میله به یکی دیگر از میله‌ها تحت شرایطی انتقال دهند، و باور داشتند که با تمام شدن انتقال قرص‌ها عمر جهان نیز به پایان خواهد رسید! میله اولیه ۶۴ قرص داشت، که بر روی هم به‌طور نزولی بر اساس اندازه‌شان چیده شده‌بودند.[3]

نمونه‌ای از برج هانوی

همانند شکل سه میله داریم. یکی از میله‌ها میله مبدأ (A)، دیگری میله کمکی (B) و دیگری میله مقصد (C) است. هدف انتقال تمام دیسک‌ها از میله مبدأ به میله مقصد با رعایت شرایط زیر است:

در هر زمان فقط یک دیسک را می‌توان جابجا نمود. نباید در هیچ زمانی دیسکی بر روی دیسک با اندازه کوچکتر قرار بگیرد.

حل معادله

هدف ما ارائه الگوریتمی است که کمترین توالی حرکت‌ها را برای انتقال دیسک‌ها به ما بدهد؛ مثلاً اگر n=۲ باشد، توالی حرکت به صورت زیر است:

حل مسئله برج هانوی با ۴ دیسک

دیسک ۱ را به میله B منتقل می‌کنیم.
دیسک ۲ را به میله C منتقل می‌کنیم.
دیسک ۱ را به میله C منتقل می‌کنیم.[4]

حل مسئله برج هانوی با ۳ دیسک

توجه داشته باشید که بر اساس قانون اول نمی‌توان به غیر از بالاترین دیسک هر میله، به دیسک دیگری از آن دسترسی پیدا کرد.

حال سؤال این است که آیا این مسئله به کمک تکنیک بازگشت قابل حل است؟ اصولاً چه مسائلی را می‌توان بازگشتی حل نمود؟

برای اینکه مسئله‌ای بتواند با روش بازگشتی حل شود باید یک ویژگی اساسی داشته باشد. مسئله اصلی (مسئله‌ای که به ما داده می‌شود) قابل خرد شدن به زیر مسئله‌هایی از همان نوع مسئله اصلی باشد، به شرطی که اندازه زیر مسئله‌های ایجاد شده کمتر باشد. آنگاه می‌توان امیدوار بود که آن را به‌طور بازگشتی حل کرد! این ویژگی در مورد مسئله برج هانوی صدق می‌کند. ایده اصلی این است که توجهمان را به جای حرکت بالاترین دیسک، روی پایین‌ترین دیسک میله متمرکز کرده، و مراحل زیر را طی می‌کنیم:

n - ۱ دیسک بالایی را با شرایط ذکر شده و به کمک میله C به میله B منتقل می‌کنیم. بزرگترین دیسک را از میله مبدأ به میله مقصد حرکت می‌دهیم.n - ۱ دیسک را که هم‌اکنون در میله B هستند با شرایط داده شده به میله مقصد انتقال می‌دهیم. می‌بینیم که توانستیم عملیات جابجا کردن n دیسک را به دو عملیات مشابه ولی با اندازه کمتر و یک عملیات ساده تقسیم کنیم. واضح است که جابجا کردن n - ۱ قرص راحتتر از جابجا نمودن n قرص است.[5]

حل مسئله با زبان‌های برنامه‌نویسی کامپیوتری

برج‌های هانوی به زبان پیتون

برنامهٔ زیر تابع راه حل بازگشتی را به زبان برنامه‌نویسی پیتون نشان می‌دهد:

A = [3, 2, 1]
B = []
C = []

def move(n, source, target, auxiliary):
    if n > 0:
        # Move n - 1 disks from source to auxiliary, so they are out of the way
        move(n - 1, source, auxiliary, target)

        # Move the nth disk from source to target
        target.append(source.pop())

        # Display our progress
        print(A, B, C, '##############', sep='\n')

        # Move the n - 1 disks that we left on auxiliary onto target
        move(n - 1, auxiliary, target, source)
# Initiate call from source A to target C with auxiliary B
move(3, A, C, B)

برج هانوی به زبان ++C

تابع بازگشتی زیر به زبان ++C ترتیب حرکت‌ها را چاپ می‌کند:

void hanoi (int nDisk, char start, char temp, char finish)

{

  if (nDisk == 1)

  cout <<start <<" --> " <<finish <<endl;

  else

  {

  hanoi (nDisk - 1, start, finish, temp);

  cout <<start <<" --> " <<finish <<endl;

  hanoi (nDisk - 1, temp, start, finish);

  }

}

برای مثال فراخوانی تابع به شکل ('hanoi(3, ‘A’, ‘B’, ‘C مسئله برج هانوی را با سه دیسک که در میله A قرار دارند و با کمک میله B به میله C منتقل خواهد شد، حل می‌کند.

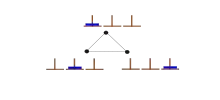
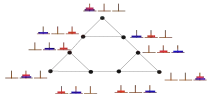
ترتیب فراخوانی‌ها برای اجرا شدن دستور

درختی که ترتیب اجرای دستورها را نشان می‌دهد

برای این که به کاهنان کمک کنیم، باید دستور ('hanoi(64, ‘A’, ‘B’, ‘C را اجرا کنیم؛ ولی چه زمانی طول می‌کشد تا این دستور اجرا شود؟ در حالت کلی می‌خواهیم بدانیم اگر تعداد دیسک‌ها n باشد، کمترین تعداد حرکت برای جابجا نمودن دیسک‌ها چقدر است؟

در ابتدا باید بررسی کنیم که آیا تابع بازگشتی فوق کمترین تعداد حرکت را چاپ می‌کند؟ جواب مثبت است؛ زیرا واضح است که برای جابجا کردن بزرگترین دیسک از پایین میله A، بقیه دیسک‌ها باید در میله B باشند. فقط در این صورت این دیسک جابجا می‌شود. در فراخوانی‌های بعدی دیسک دوم از نظر بزرگی جابجا می‌شود و الی آخر. پس در این فراخوانی‌ها جابجایی بیهوده‌ای صورت نمی‌گیرد. همچنین توالی حرکت‌ها برای هر n منحصربه‌فرد است؛ یعنی برای یک n دو توالی متمایز از جابجایی‌ها وجود ندارد که تعداد جابجایی آن‌ها کمتر یا مساوی این حالت باشد.

حال به مسئله مرتبه اجرایی مسئله می‌پردازیم: فرض کنیم (T(n تعداد حرکت‌های لازم جهت انتقال n دیسک به مقصد باشد. بر اساس توضیحات فوق (T(n - ۱ حرکت برای انتقال n - ۱ دیسک به میله کمکی، یک حرکت برای انتقال بزرگترین دیسک به میله مقصد، و باز (T(n - ۱ حرکت برای انتقال n - ۱ دیسک موجود در میله کمکی به میله مقصد نیاز است. پس می‌توان نوشت:

T(n) =2 T(n - ۱) + ۱

با حل این رابطه بازگشتی داریم:

T(n) = 2ⁿ-۱

همان‌طور که مشاهده می‌کنیم مرتبه اجرایی این الگوریتم (O(2ⁿ است که هرچند مرتبه مناسبی نیست، این روش حداقل تعداد حرکتهای ممکن را می‌دهد.

اگر فرض کنیم کاهنان با سرعت عمل زیاد توانسته باشند به صورت شبانه‌روزی و نسل به نسل در هر دو ثانیه یک قرص را جابجا کنند، برای انتقال تمامی ۶۴ قرص به میله مقصد، در حدود ۱٫۱۶۹ ترلیون (میلیون میلیون) سال زمان لازم دارند!

در واقع ما از روش Divide and Conquer یا حل و تقسیم برای ارائه راه حل استفاده نموده‌ایم. اما چون در تقسیم مسئله اصلی به دو زیر مسئله، اندازه ورودی‌های زیر مسئله‌ها نزدیک به اندازه ورودی اصلی هستند، کارایی الگوریتم مطلوب نیست.

حل مسئله برج هانوی به روش غیربازگشتی

این مسئله علاوه بر روش تابع بازگشتی راه حلهای غیربازگشتی نیز دارد. در بالا به این نتیجه رسیدیم که بهترین راه حل برای جابجا کردن n دیسک ۲n - ۱ حرکت نیاز دارد. در نتیجه مرتبه راه حلهای آن در بهینه‌ترین حالت، چه بازگشتی و چه غیربازگشتی، از مرتبه (O(2n خواهد بود. اما آنچه که راه حل بازگشتی و غیربازگشتی را از هم متمایز می‌کند مرتبه فضای مصرفی آن است. حل بازگشتی مسئله، فراخوانی‌های تو در تو و فضای پشته از مرتبه (O(n نیاز دارد. در حالی که می‌توان با استفاده از روش غیربازگشتی این مرتبه را به (O(1 کاهش داد. البته این مسئله تنها دلیل بررسی روش غیربازگشتی نیست. تبدیل مرتبه مصرف فضا از (O(n به (O(1 زمانی که مرتبه اجرایی الگوریتم (O(2n است چندان قابل توجه نیست. دلیل دیگر می‌تواند این باشد که برخی زبانهای برنامه‌نویسی از فراخوانی بازگشتی توابع پشتیبانی نمی‌کنند و مجبور به استفاده ار روش‌های غیربازگشتی هستند. اما دلیل اصلی این است که با بررسی این روش‌ها تمرین کوچکی برای تبدیل الگوریتمهای بازگشتی به غیربازگشتی انجام می‌دهیم.

تا کنون چندین روش مختلف جهت پیاده‌سازی غیربازگشتی حل مسئله برج هانوی ارائه شده‌است، که ما در اینجا دو روش را معرفی کرده، و تنها یکی از آن‌ها را به‌طور کامل بررسی می‌کنیم. توجه داشته باشید که همه جزئیات حل مسئله به صورت دقیق و مشروح مطرح نمی‌شود، و استدلال قسمتی از نتیجه‌گیری‌ها به عنوان تمرین به شما واگذار می‌شود.

روش اول:

حل مسئله برج هانوی را می‌توان معادل پاسخ دادن به این سؤال دانست که: در هر مرحله کدام دیسک به کدام میله منتقل می‌شود؟

کدام دیسک؟

فرض کنیم دیسکهایی به شعاع y ,x و z که رابطه x <y <z را با هم دارند، کوچکترین دیسک هر میله باشند. به عبارت دیگر این سه دیسک، بالاترین دیسکهای میله‌ها هستند که قابلیت جابجایی دارند. اگر میله‌ای شامل هیچ دیسکی نباشد، دیسکی با شعاع بی‌نهایت را برای آن در نظر می‌گیریم. حال به استدلالهای منطقی زیر توجه کنید:

استدلال ۱: x برابر ۱ است. چرا که بر اساس قوانین حاکم بر مسئله، هیچ دیسکی نمی‌تواند روی دیسک ۱ قرار بگیرد. در نتیجه این دیسک همیشه بالاترین دیسک موجود در یکی از میله‌ها است.

استدلال ۲: در اولین مرحله دیسک ۱ جابجا می‌شود. در آغاز همه دیسکها روی یک میله قرار دارند که دیسک ۱ بالاترین دیسک آن است.

استدلال ۳: دیسکهایی که طی دو مرحله متوالی جابجا می‌شوند حتماً متمایز هستند. این مسئله از بهینه بودن راه حل ما ناشی می‌شود. اگر قرار باشد طی دو مرحله متوالی یک دیسک خاص را جابجا کنیم، می‌توانیم دو مرحله را با هم ادغام کرده و کل جابجایی را یکجا انجام دهیم.

استدلال ۴: با توجه به قوانین حاکم بر مسئله، دیسک z نمی‌تواند حرکت کند. چرا که دیسکهای x و y هر دو از آن کوچکتر هستند.

استدلال ۲ می‌گوید که اولین حرکت همیشه با دیسک ۱ است. استدلال ۳ می‌گوید حرکت بعدی با دیسکی غیر از دیسک ۱ است. استدلال ۴ می‌گوید این دیسک نمی‌تواند بزرگترین دیسک موجود در بالای میله‌ها باشد. پس در مرحله بعدی دیسک y جابجا خواهد شد؛ و بالاخره حرکت بعدی باز هم با دیسک ۱ است (چرا؟).

پس با بررسی منطقی خود به این نتیجه رسیدیم که دیسک ۱ و دیسکی که بزرگترین دیسک در آن مرحله نیست، به صورت متناوب جابجا می‌شوند. مراحل با شماره فرد برای دیسک ۱، و مراحل با شماره زوج برای دیسک y.

کدام میله؟

حال که می‌دانیم در هر مرحله کدام دیسک جابجا می‌شود، به سراغ میله مقصد می‌رویم. در مراحل زوج که دیسک y منتقل خواهد شد، تشخیص میله مقصد بسیار آسان است. چرا که روی یکی از میله‌ها دیسک ۱ قرار دارد که دیسک y نمی‌تواند روی آن قرار بگیرد. در نتیجه به تنها میله باقی‌مانده (میله دیسک z) منتقل می‌شود. در مورد مراحلی هم که دیسک ۱ قرار است جابجا شود، می‌توان اینطور استدلال کرد:

فرض کنیم دیسک ۱ روی میله A قرار داشته باشد و آن را به میله C منتقل کنیم. در مرحله بعدی دیسک y جابجا می‌شود؛ و در مرحله بعد باز هم دیسک ۱ باید جابجا شود. حال اگر این دیسک را به میله A بازگردانیم، به نوعی کار اضافی و بازگشت به عقب انجام داده‌ایم. برای آشکار شدن این موضوع کافی است مسئله برج هانوی را با دو دیسک حل کنید، و در حرکت دوم دیسک ۱، آن را به میله‌ای بازگردانید که از آن آمده بود. پس می‌توان گفت در حرکتهای متوالی، دیسک شماره ۱ به میله‌ای حرکت می‌کند که از آن به میله فعلی خود نیامده است. این مسئله نه تنها در مورد دیسک ۱، که در مورد همه دیسکها صادق است؛ یعنی همه دیسکها در حرکتهای خود به سمت میله‌ای می‌روند که در حرکت قبلی خود از آن نیامده‌اند. اما لحاظ کردن این شرط برای این دیسکها لازم نیست. چرا که در هر مرحله، تنها یک انتخاب برای حرکت خود دارند.

تنها مسئله باقی‌مانده، میله مقصد دیسک ۱ در اولین حرکت خود است. زمانی که این دیسک اولین حرکت خود را انجام می‌دهد، نمی‌توان از استدلال فوق برای تشخیص میله مقصد استفاده کرد (چرا!؟). استدلال این قسمت را هم که چندان دشوار نیست به شما وا می‌گذاریم و تنها به بیان نتیجه می‌پردازیم: اگر n (تعداد دیسکها) زوج باشد، دیسک ۱ در اولین حرکت به میله کمکی (یعنی میله B)، و در غیراینصورت به میله مقصد (یعنی میله C) منتقل می‌کنیم.

به این ترتیب حل مسئله برج هانوی به صورت غیربازگشتی به صورت کامل پیاده‌سازی می‌شود. حال می‌دانیم که در هر مرحله کدام دیسک به کدام میله منتقل می‌شود. تعداد مراحل هم همواره برابر ۲n - ۱ است. پیاده‌سازی کد این الگوریتم را نیز به شما وا می‌گذاریم تا با کار روی آن به خوبی بر الگوریتم تشریح شده مسلط شوید.

روش دوم:

یکی دیگر از روش‌های پیاده‌سازی غیربازگشتی حل مسئله برج هانوی از الگوریتم زیر تبعیت می‌کند:

void hanoi (int nDisk, char start, char temp, char finish)
{
  int max = nDisk;
  char dest = finish;
  int disk = max;
  while(true)
  {
  while(disk> 0)
  {
  if(moving disk succeeds)
  {
  if(disk == max)
  {
  max--;
  if(max == 0)
  {
  return;
  }
  }
  dest = the final place of max;
  }
  else
  {
  dest = the alternative place between dest and the current place of disk;
  }
  disk--;
  }
  p and q = the places different of dest;
  disk = the smaller of the disks on top of p and q;
  dest = the place between p and q with greater disk on top;
  }
}

در پایان توجه داشته باشید که دو روش ذکر شده، تنها روش‌های پیاده‌سازی غیربازگشتی حل مسئله نیستند.

برنامه برج هانوی به زبان c:

# include <stdlib.h>
# include <conio.h>
# define COUNT 8

enum Bar{L,C,R};
struct disk{int Size,Color;};
struct stack{int i; disk *Disks;};
void transfer(int,Bar,Bar,Bar);
void init(); // Init bars
void MoveDisk(Bar from,Bar to);
void DrawBars();
stack Bars[3]={ {0,{0}} ,{0,{0}}, {0,{0}} };
int main(void)
{
 textmode(C4350);
 clrscr();
 init();
 DrawBars();
 transfer(COUNT,L,R,C);
 getch();
 return 0;
}
char ConvertBarEnum2Char(Bar E){
 char r=0;
 switch (E) {
 case L: r='L'; break;
 case C: r='C'; break;
 case R: r='R'; break;
 }
 return r;
}

void msg(Bar from,Bar to){
 gotoxy(25,4);
 textattr(15|16*0);
 cprintf("Press anykey to move from %c to %c",ConvertBarEnum2Char(from),ConvertBarEnum2Char(to));
 gotoxy(37,5);
 cprintf("Esc = Exit");
}

void transfer(int n,Bar from,Bar to,Bar temp){
if(n>0){
 transfer(n-1,from,temp,to);
 msg(from, to);
 MoveDisk(from,to);
 transfer(n-1,temp,to,from);
 }
}
void init(){
Bars[L].Disks=new disk[COUNT];
for(int i=0;i<COUNT;i++){
Bars[L].Disks[i].Size=COUNT-i+1;
Bars[L].Disks[COUNT-i-1].Color=i+1;
}
Bars[L].i=COUNT-1;

Bars[R].Disks=new disk[COUNT];
for(i=0;i<COUNT;i++){
Bars[R].Disks[i].Size=0;
Bars[R].Disks[i].Color=0;
}
Bars[R].i=-1;

Bars[C].Disks=new disk[COUNT];
for(i=0;i<COUNT;i++){
Bars[C].Disks[i].Size=0;
Bars[C].Disks[i].Color=0;
}
Bars[C].i=-1;
}

void MoveDisk(Bar from,Bar to){
char kb=getch();
if(kb==27) exit(1);
Bars[to].Disks[++(Bars[to].i)]= Bars[from].Disks[(Bars[from].i)--];
clrscr();
DrawBars();
}
void me(){
char c;
for(int i=0;str[i];i++){
c=i%14+1;
if(c==1)c=2;
textattr(c|16);
cprintf("%c",str[i]);
}
}

void DrawBars(){
int n=0;
for(int j=0;j<3;j++){
for(int i=0;i<=Bars[j].i;i++){
gotoxy(1+j*27,24-i);
textattr(Bars[j].Disks[i].Color|16*0);
for(n=0;n<28 && n-13<Bars[j].Disks[i].Size ;n++){
if(n<14-Bars[j].Disks[i].Size)
cprintf("%s"," ");
else
cprintf("%s","ـ");
}
}
textattr(15|16*0);
for(n=0;n<15;n++){
gotoxy(1+j*27+13,n+10);
cprintf("%s",";");
}
}
gotoxy(5,28);
me();
}

منابع

شهریاری، پرویز (۱۳۵۲). در پی فیثاغورث. تهران: انتشارات امیرکبیر. صص. ۲۵۸.
Hofstadter، Douglas R. (۱۹۸۵). Metamagical Themas: Questing for the Essence of Mind and Pattern. Basic Books. شابک ۹۷۸-۰-۴۶۵-۰۴۵۴۰-۲.
Spitznagel، Edward L. (۱۹۷۱). Selected topics in mathematics. Holt, Rinehart and Winston. صص. ۱۳۷. شابک ۹۷۸-۰-۰۳-۰۸۴۶۹۳-۹.
Troshkin, M. "Doomsday Comes: A Nonrecursive Analysis of the Recursive Towers-of-Hanoi Problem". Focus (به Russian): 10–14.
Mayer، Herbert (۱۹۸۴). «Towers of Hanoi Revisited». SIGPLAN Notices: ۸۰–۸۴.

مشارکت کنندگان ویکی‌پدیا(Tower of Hanoi)، در دانشنامه ویکی‌پدیای انگلیسی. بازبینی در ۳۰ می ۲۰۱۹.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] شهریاری، پرویز (۱۳۵۲). در پی فیثاغورث. تهران: انتشارات امیرکبیر. صص. ۲۵۸.

[2] Hofstadter، Douglas R. (۱۹۸۵). Metamagical Themas: Questing for the Essence of Mind and Pattern. Basic Books. شابک ۹۷۸-۰-۴۶۵-۰۴۵۴۰-۲.

[3] Spitznagel، Edward L. (۱۹۷۱). Selected topics in mathematics. Holt, Rinehart and Winston. صص. ۱۳۷. شابک ۹۷۸-۰-۰۳-۰۸۴۶۹۳-۹.

[4] Troshkin, M. "Doomsday Comes: A Nonrecursive Analysis of the Recursive Towers-of-Hanoi Problem". Focus (به Russian): 10–14.

[5] Mayer، Herbert (۱۹۸۴). «Towers of Hanoi Revisited». SIGPLAN Notices: ۸۰–۸۴.