برش بیشینه

برش بیشینه در یک گراف، برشی است که اندازه آن از تمام برش‌های ممکن در گراف بزرگتر است.

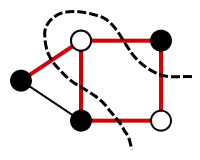
یک برش بیشینه.

تعریف

در نظریه گراف، برش، تقسیم رئوس گراف به دو زیرمجموعه جدا از هم می‌باشد.

"مجموعه-برش" در یک برش، مجموعه یال‌هایی است که دو سر آن‌ها، هر یک، در یک بخش است.

یال‌های "عبور" از یک برش به یال‌هایی گویند که در مجموعه-برش آن باشند.

در گراف بی وزن، اندازه یا وزن یک برش، تعداد یال‌های عبور برش است. و در گراف‌های وزن دار، جمع وزن یال‌های عبور است.

برش بیشینه در یک گراف، برشی است که اندازه آن از تمام برش‌های ممکن در گراف بزرگتر است.

بیان ساده برش بیشینه: برشی که تعداد یال‌های عبور آن بیشینه باشد.

نمونه پیشرفته این مسئله، برش بیشینه وزن دار نامیده می‌شود. در این مورد، به هر یال یک عدد نسبت داده می‌شود (وزن یال) و هدف، یافتن برشی است که وزن یال‌های عبوری آن بیشینه باشد. توجه شود که وزن یال‌ها در این مسئله باید مثبت باشد، چون مقادیر منفی حاصل جمع را تضعیف می‌کنند.

پیچیدگی الگوریتم

به دلیل اینکه مسئله برش بیشینه ان‌پی کامل است، هیچ الگوریتمی از مرتبه چند جمله‌ای برای برش بیشینه شناخته نشده است. این در حالی است که این مرتبه برای یافتن برش بیشینه در گراف‌های سطحی موجود است.

الگوریتم‌های تخمین

"الگوریتم تخمین (۰٫۵)" تصادفی و ساده‌ای بری این مسئله وجود دارد: برای هر راس یک سکه در نظر می‌گیریم تا تصمیم بگیریم که به کدام قسمت آن را اختصاص دهیم. انتظار داریم، نیمی از یال‌ها، یال‌های برش باشند. این الگوریتم می‌تواند مجدداً به صورت تصادفی با تابع احتمال شرطی بیان شود؛ بدین منظور، "الگوریتم تخمین (۰٫۵)" ساده و معینی وجود دارد:

گراف ${\displaystyle G=(V,E)\!}$ داده شده است. با تقسیم دلخواه از ${\displaystyle V\!}$ شروع کنید ودر صورت پیشرفت روند حل مسئله، َ یک راس را از یک طرف به طرف دیگر جابجا کنید. تا وقتی که چنین راسی موجود نباشد، این کار را ادامه دهید. این الگوریتم، برش را با حداقل یک عمل در هر گام، جلو می‌برد، پس تعداد تکرار این عمل، از مرتبه یا پیچیدگی زمانی ${\displaystyle O(|E|)\!}$ است. وقتی که الگوریتم متوقف می‌شود، حداقل نیمی از یال‌های هر راس ${\displaystyle v\!}$، در برش قرار دارد. (در غیر این صورت، برای پیشرفت در حل مسئله باید راس ${\displaystyle v\!}$ را به زیر مجموعه دیگر، منتقل کنیم.) بنابراین، اندازه برش حداقل ${\displaystyle 0.5|E|\!}$ است.

بهترین الگوریتم برش بیشینه شناخته شده، "الگوریتم تخمین(۰٫۸۷۸)" می‌باشد که توسط ژئومنز و ویلیامسون ارائه شده است. گفتنی است که این بهترین تخمین ممکن برای برش بیشینه است.

بزرگترین زیر گراف دوبخشی

برش، گراف را به گراف دوبخشی تبدیل می‌کند. در نتیجه مسئله یافتن برش بیشینه، معادل مسئله یافتن زیر گراف دو بخشی با بیشترین یال می‌باشد.

فرض کنید ${\displaystyle G=(V,E)\!}$ گراف اصلی و ${\displaystyle H=(V,X)\!}$ زیر گرافی دوبخشی از ${\displaystyle G\!}$ است. پس بخش ${\displaystyle (S,T)\!}$ از ${\displaystyle V\!}$ وجود دارد که هر یال در ${\displaystyle X\!}$ یک انتها در ${\displaystyle S\!}$ و یک انتها در ${\displaystyle T\!}$ داشته باشد. وگرنه، برشی در ${\displaystyle H\!}$ وجود دارد که "مجموعه-برش" شامل یال‌های ${\displaystyle X\!}$ می‌باشد. بنابراین، برشی در ${\displaystyle G\!}$ وجود دارد که ${\displaystyle X\!}$، زیر مجموعه "مجموعه-برش" ${\displaystyle G\!}$ می‌باشد.

به طور خلاصه، اگر زیر گراف دو بخشی با ${\displaystyle k\!}$ یال وجود داشته باشد، برشی با حداقل ${\displaystyle k\!}$ "یال عبوری" وجود دارد؛ و اگر برشی با ${\displaystyle k\!}$ یال عبوری وجود داشته باشد، یک زیر گراف دو بخشی با ${\displaystyle k\!}$ یال موجود می‌باشد. پس مسئله پیدا کردن زیر گراف دو بخشی بیشینه، معادل مسئله پیدا کردن برش بیشینه است.

صفحات مربوط

• برش کمینه

منابع

• Trevisan, Luca; Sorkin, Gregory; Sudan, Madhu; Williamson, David (2000), "Gadgets, Approximation, and Linear Programming", Proceedings of the 37th IEEE Symposium on Foundations of Computer Science: 617–626.
• Motwani, Rajeev; Raghavan, Prabhakar (1995), Randomized Algorithms, Cambridge.
• Arora, Sanjeev; Rao, Satish; Vazirani, Umesh (2009), "Expander flows, geometric embeddings and graph partitioning", J. ACM, ACM, 56 (2): 1–37, ISSN 0004-5411
• سایت http://en.wikipedia.org/wiki/Cut_(graph_theory):
• سایت http://en.wikipedia.org/wiki/Max_cut