گراف دوبخشی
در نظریهٔ گراف (یکی از شاخههای ریاضیات)، گراف دوبخشی گرافی است که راسهایش را میتوان به دو مجموعهٔ مجزا مثل و تقسیم کرد، طوری که هر یال از آن گراف، یک راس از را به یک راس از متصل میکند. معادلا، گراف دوبخشی گرافی است که دور به طول فرد ندارد.

میتوان به و به چشم یک رنگآمیزی مجاز گراف نگاه کرد: اگر همهٔ راسهای مجموعهٔ را آبی و همهٔ راسهای مجموعهٔ را سبز کنیم، دو راس انتهایی هر یال رنگهای متفاوتی خواهند داشت که نشاندهندهٔ یک رنگآمیزی مجاز برای گراف است. از طرف دیگر، این نوع رنگآمیزی برای گرافهای غیر دوبخشی (مثل مثلث) غیرممکن است. مثلاً در مثلث، اگر یک راس را به رنگ آبی و دیگری را به رنگ سبز درآوریم، راس سوم را نمیتوانیم با هیچکدام از این رنگها رنگ کنیم، چون این راس به هر دو راس دیگر متصل است.
گراف دو بخشی را معمولاً به صورت نشان میدهیم که و دو بخش گراف و مجموعهٔ یالهای گراف است. اگر یک گراف دوبخشی همبند نباشد، ممکن است بتوان راسهای آن را به شیوههای مختلف به دو بخش تقسیم نمود (یعنی ممکن است و یکتا نباشند). در این صورت نمایش سودمند واقع میشود؛ چون به کمک آن میتوان یک حالت خاص تقسیم رئوس گراف به دو بخش را از بقیهٔ حالات متمایز کرد. اگر ، گراف را گراف دوبخشی متوازن مینامیم. اگر درجهٔ تمام راسهای با هم و نیز درجهٔ تمام راسهای با هم برابر باشد، گراف را گراف دوبخشی شبه منتظم مینامیم.
مثالها
وقتی رابطهٔ بین دو گروه مختلف از اشیا را مدلسازی میکنیم، معمولاً گرافهای دوبخشی به طور طبیعی ظاهر میشوند. به عنوان مثال، فرض کنید یک گراف داشته باشیم که راسهای آن نمایانگر بازیکنان فوتبال و باشگاهها باشند. یک بازیکن را به یک باشگاه وصل میکنیم، اگر آن بازیکن برای آن باشگاه بازی کرده باشد. این گراف نمونهای از شبکههای وابستگی (affiliation network) است. این شبکهها نوعی گراف دوبخشی هستند و از آنها در آنالیز شبکهٔ اجتماعی (social network analysis) استفاده میشود.
مثال دیگری که در آن، گراف دوبخشی به طور طبیعی ظاهر میشود، مسألهٔ بهینهسازی راهآهن است (NP-complete) که در آن، ورودی برنامهٔ حرکت زمانی قطارها و توقف آنها است و هدف یافتن کوچکترین مجموعهٔ ممکن از ایستگاههای قطار است، طوری که هر قطار در حداقل یکی از این ایستگاهها توقف کند. این مسئله را میتوان به صورت یافتن یک مجموعهٔ غالب در یک گراف دوبخشی مدلسازی کرد که در این گراف برای هر قطار و هر ایستگاه یک راس وجود دارد و یک قطار به یک ایستگاه وصل میشود، اگر آن قطار در آن ایستگاه توقف کند.
مثالهای انتزاعیتر به شرح زیر میباشند:
- هر درخت دوبخشی است.
- دور به طول زوج دوبخشی است.
- هر گراف مسطح که طول تمام وجههایش زوج است، دوبخشی میباشد. حالتهای خاص این مورد، گرافهای شبکهای (grid graph) و گرافهای مربعی (squaregraph) هستند که در آنها هر وجه داخلی ۴ یال دارد و هر راس داخلی ۴ یا تعداد بیشتری همسایه دارد.
- گراف کامل دوبخشی که از دو بخش با تعداد راسهای و تشکیل شده است و با Km,n نمایش داده میشود، گراف دوبخشی است که و مجموعههای متمایز از راسهای گراف، به ترتیب با اندازههای و هستند و هر راس از را به تمام راسهای وصل میکند. پس نتیجه میشود که Km,n، یال دارد. گرافهای تاجی شکل (crown graph) ارتباط نزدیکی با گرافهای کامل دوبخشی دارند و در واقع با حذف یالهای یک تطابق کامل از گراف کامل دوبخشی به دست میآیند.
- گرافهای k-مکعب، partial cube و گرافهای میانه (median graphs) دوبخشی هستند. در این گرافها، راسها را میتوان با رشتههایی از ۰ و ۱ به طول برابر برچسبگختلاف داشته باشند. یک روش تقسیم رئوس اینگونه گرافها به دوبخش، به این صورت است که رئوسی را که تعداد یکهای موجود در رشتهٔ متناظر با آنها فرد است، در یک دسته و رئوسی را که تعداد یکهای موجود در رشتهٔ متناظر با آنها زوج است، در دستهای دیگر قرار میدهیم. درختها و گرافهای مربعی (squaregraphs) نوعی از گرافهای میانهای (median graphs) هستند و هر گراف میانهای (median graph) یک partial cube است.
خواص
توصیف
گرافهای دوبخشی را به چند روش میتوان توصیف کرد:
- یک گراف دوبخشی است، اگر و تنها اگر شامل دور فرد نباشد.
- یک گراف دوبخشی است، اگر و تنها اگر ۲-رنگپذیر باشد (یعنی عدد رنگی آن کمتر یا مساوی ۲ باشد).
- Spectrum یک گراف متقارن است، اگر و تنها اگر آن گراف دوبخشی باشد.
قضیهٔ König و گرافهای آرمانی
در گرافهای دوبخشی، اندازهٔ کوچکترین پوشش راسی برابر با اندازهٔ بزرگترین تطابق است:این قضیهٔ König است. صورت دیگر و معادل این قضیه، این است که مجموع اندازهٔ بزرگترین مجموعهٔ مستقل و اندازهٔ بزرگترین تطابق برابر با تعداد رئوس است. در هر گرافی که راس منزوی نداشته باشد، مجموع اندازهٔ کوچکترین پوشش یالی و اندازهٔ بزرگترین تطابق برابر با تعداد رئوس است. اگر این تساوی را با قضیهٔ König ترکیب کنیم، به این نتیجه میرسیم که در گرافهای دوبخشی، اندازهٔ کوچکترین پوشش یالی برابر با اندازهٔ بزرگترین مجموعهٔ مستقل است، و مجموع اندازهٔ کوچکترین پوشش یالی و اندازهٔ کوچکترین پوشش راسی برابر با تعداد راسها است.
نتایج دیگری که از قضیهٔ König به دست میآیند، به گرافهای آرمانی مربوط میشوند: هر گراف دوبخشی، مکمل هر گراف دوبخشی، line graph هر گراف دوبخشی و مکمل line graph هر گراف دوبخشی همگی آرمانی هستند. آرمانی بودن گرافهای دوبخشی را به راحتی میتوان بررسی کرد (عدد رنگی آنها دو است و اندازهٔ بزرگترین خوشهٔ آنها هم دو است) اما آرمانی بودن مکمل یک گراف دوبخشی چندان بدیهی نیست، و در واقع صورت دیگری از قضیهٔ König است. این یکی از نتایجی بود که انگیزهٔ تعریف گرافهای آرمانی را به وجود آورد. آرمانی بودن مکمل line graph گرافهای آرمانی هم نتیجهٔ دیگری است که از قضیهٔ König به دست میآید، و آرمانی بودن خود line graphها بیان دیگری از قضیهای قدیمیتر، از König میباشد که هر گراف دوبخشی یک رنگآمیزی یالی با استفاده از تعدادی رنگ که تعداد آنها برابر با بیشترین درجهٔ گراف است، دارد.
بنابر نظریهٔ قوی گرافهای آرمانی (strong perfect graph theorem)، گرافهای آرمانی خاصیتی شبیه به گرافهای دوبخشی دارند: یک گراف دوبخشی است، اگر و تنها اگر شامل هیچ زیرگرافی به شکل دور فرد نباشد، و یک گراف آرمانی است، اگر و تنها اگر هیچ زیرگراف القایی از آن به شکل دور فرد یا مکمل آن نباشد. گرافهای دوبخشی، line graph گرافهای دوبخشی، و مکمل آنها، ۴ رده از ۵ ردهٔ اصلی گرافهای آرمانی را که در اثبات قضیهٔ قوی گرافهای آرمانی (strong perfect graph theorem)از آنها استفاده میشود، تشکیل میدهند.
ارتباط با ابرگرافها (hyphergraphs) و گرافهای جهتدار
ماتریس مجاورت گراف دوبخشی یک ماتریس شامل ۰ و ۱ با اندازهٔ است که در هر خانهٔ آن، اگر دو راس مربوط به آن خانه مجاور باشند، ۱ و در غیر این صورت صفر قرار داده میشود. از ماتریس مجاورت گرافهای دوبخشی میتوان برای نشان دادن همارزی بین گرافهای دوبخشی، ابرگرافها، و گرافهای جهتدار استفاده کرد.
یک ابرگراف (hypergraph) یک ساختار ترکیبیاتی است که همانند گرافهای غیر جهتدار، تعدادی راس و یال دارد، ولی هر یال میتواند مجموعهٔ دلخواهی از رئوس باشد (به جای این که دقیقاً از دو راس تشکیل شده باشد). از گراف دوبخشی میتوان برای مدلسازی ابرگرافها استفاده نمود که در آن مجموعهٔ راسهای ابرگراف و مجموعهٔ ابریالها (hyperedges) است و شامل یک یال از یک راس ابرگراف مثل به یک ابریال مثل است، اگر یکی از نقاط انتهایی باشد. با این تناظر، ماتریس مجاورت یک گراف دوبخشی دقیقاً همان ماتریس وقوع ابرگراف متناظر با آن است. به عنوان یک حالت خاص از این تناظر بین گرافهای دوبخشی و ابرگرافها، هر گراف چندگانه (گرافی که ممکن است بین دو راس از آن دو یا چند یال وجود داشته باشد) را میتوان به صورت یک ابرگراف در نظر گرفت که در آن برخی ابریالها مجموعهٔ یکسانی از راسها را دارند و این ابرگراف را میتوان با یک گراف دوبخشی نشان داد که یال چندگانه ندارد و همهٔ راسهای یک طرف آن از درجهٔ ۲ هستند.
تفسیر مشابهی از ماتریسهای مجاورت برای برقراری تناظر یک به یک بین گرافهای جهتدار (که در آنها راسها برچسبگذاری شدهاند و طوقه مجاز است) و گرافهای دوبخشی متوازن (balanced bipartite graphs) که در آنها تعداد رئوس موجود در دو بخش با هم برابر است، به کار میرود. ماتریس مجاورت یک گراف جهتدار با راس میتواند هر ماتریس شامل ۰ و ۱ باشد که آن را میتوان به عنوان ماتریس مجاورت یک گراف دوبخشی با راس در هر بخش در نظر گرفت. در این فرایند، گراف دوبخشی به دست آمده را bipartite double cover گراف جهتدار مینامیم.
الگوریتمها
بررسی دو بخشی بودن یک گراف
میتوانیم در زمان خطی (با استفاده از الگوریتم جستجوی عمق-اول (depth-first search)) تشخیص دهیم که یک گراف دوبخشی است یا نه و یک ۲-رنگآمیزی از آن گراف را برگردانیم (اگر دوبخشی است) یا یک دور فرد از آن گراف را برگردانیم (اگر دوبخشی نیست). ایدهٔ اصلی این است که در جهت پیمایش درخت جستجوی عمق-اول حرکت کنیم و به هر راس رنگی را نسبت دهیم که با رنگ پدرش متفاوت است. این کار قطعاً یک ۲-رنگآمیزی از یک زیر درخت فراگیر گراف، که شامل یالهایی است که راسها را به پدرانشان وصل میکنند، به دست میدهد ولی این رنگآمیزی ممکن است باعث شود دو راس انتهایی یکی از یالهای گراف که در این زیر درخت فراگیر نیامده، همرنگ شوند. در درخت جستجوی عمق-اول، یکی از دو راس انتهایی هر یالی که در درخت نیامده، جد راس دیگر میباشد و وقتی الگوریتم جستجوی عمق-اول یالی از این دست را پیدا میکند، باید چک کند که دو راس انتهایی آن همرنگ نباشند. اگر همرنگ باشند، مسیر درون درخت از راس جد به راس نوه به همراه یالی که راسهایش اشتباه رنگ شدهاند، تشکیل یک دور به طول فرد میدهند که به همراه این نتیجه که گراف دوبخشی نیست، توسط الگوریتم بازگردانده میشود. اما اگر الگوریتم بدون پیدا کردن چنین دور فردی متوقف شود، در این صورت تمام رئوس باید به طور مجاز رنگآمیزی شده باشند و الگوریتم، رنگآمیزی انجام شده را به همراه این نتیجه که گراف دوبخشی است، بازمیگرداند.
میتوان به جای استفاده از الگوریتم جستجوی عمق-اول، از الگوریتم جستجوی سطح-اول (breadth-first search) هم استفاده کرد. باز هم مثل قبل، به هر راس در درخت جستجوی سطح-اول، رنگی را نسبت میدهیم که با رنگ پدرش در این درخت متفاوت باشد. اگر وقتی که یک راس رنگ میشود، یالی در گراف موجود باشد که این راس را به یک راس قبلاً رنگ شده با رنگ مشابه وصل کند، این یال به همراه مسیرهایی در درخت جستجوی سطح-اول که این دو راس را به کوچکترین جد مشترکشان (lowest common ancestor) وصل میکنند، تشکیل یک دور به طول فرد میدهند. اگر الگوریتم بدون پیدا کردن دور فردی با این روش متوقف شود، رنگآمیزی انجام شده مجاز است و میتوان نتیجه گرفت که گراف دوبخشی است.
برای گراف برخورد پارهخط یا دیگر شکلهای ساده در صفحهٔ اقلیدسی، میتوان در زمان بررسی کرد که گراف دوبخشی است یا نه و یک ۲-رنگآمیزی گراف یا یک دور فرد از آن را برگرداند، با این که ممکن است خود گراف حتی یال داشته باشد.
Odd cycle transversal
Odd cycle transversal یک مسألهٔ الگوریتمیک NP-Complete است که به عنوان ورودی یک گراف و یک عدد دریافت میکند و بررسی میکند که آیا مجموعهای از راس از وجود دارند که حذف آنها از باعث دوبخشی شدن گراف حاصل شود یا نه. این مسئله fixed-parameter tractable است، یعنی الگوریتمی وجود دارد که زمان اجرای آن میتواند به حاصلضرب یک تابع چندجملهای از اندازهٔ گراف و یک تابع بزرگتر با متغیر محدود شود. به طور دقیقتر، زمان اجرای این الگوریتم است.
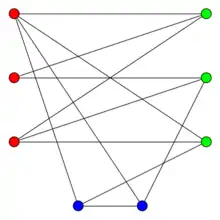
اسم odd cycle transversal از اینجا میآید که یک گراف دوبخشی است، اگر و تنها اگر شامل دور فرد نباشد؛ بنابراین، برای حذف کردن تعدادی راس از گراف و به دست آوردن یک گراف دوبخشی، نیاز داریم که «همهٔ دورهای فرد را قطع کنیم»، یا به عبارتی یک مجموعهٔ odd cycle transversal پیدا کنیم. در شکل نشان داده شده، میتوان مشاهده کرد که هر دور فرد در گراف، شامل راسهای آبی است و بنابراین حذف این راسها از گراف، آن را دوبخشی میکند.
مسألهٔ دوبخشی کردن یالی (edge bipartization) یک مسألهٔ الگوریتمیک است که در آن به دنبال حذف کردن کمترین تعداد یالهای ممکن از گراف هستیم، طوری که گراف حاصل دوبخشی شود.
تطابق
یک تطابق در گراف، زیر مجموعهای از یالهای آن است که در آن هیچ دو یالی راس مشترک ندارند. برای بسیاری از مسئلههای مربوط به تطابق مثل تطابق بیشینه (یافتن تطابقی که بیشترین تعداد یالهای ممکن را شامل میشود)، تطابق با وزن بیشینه و ازدواج پایدار (stable marriage)، الگوریتمهایی با زمان چندجملهای وجود دارند. در بسیاری از موارد مسائل تطابق را میتوان با استفاده از گرافهای دوبخشی راحتتر حل کرد (تا این که بخواهیم از گرافهای غیر دوبخشی استفاده کنیم) و بسیاری از الگوریتمهای تطابق مثل الگوریتم Hopcroft-Karp برای یافتن تطابق با اندازهٔ بیشینه فقط روی ورودیهای دوبخشی درست کار میکنند.
به عنوان یک مثال ساده، فرض کنید مجموعهٔ شامل تعدادی فرد، به دنبال یافتن شغل بین مجموعهٔ از تعدادی شغل هستند و همهٔ افراد برای همهٔ شغلها مناسب نیستند. این وضعیت را میتوان با گراف دوبخشی مدلسازی کرد که در آن هر یال، یک جویندهٔ شغل را به شغلهای مناسبش وصل میکند. تطابق کامل معادل با این است که همزمان برای همهٔ افراد شغل پیدا کنیم و همچنین همهٔ شغلها را پر کنیم. قضیهٔ ازدواج ویژگیای را برای گرافهای دوبخشی مطرح میکند که در گرافهای دوبخشی دارای آن ویژگی میتوان تطابق کامل پیدا کرد.
روش تجزیهٔ Dulmage-Mendelsohn یک تجزیهٔ ساختاری گراف دو بخشی است که در یافتن تطابقهای بیشینه مفید میباشد.
سایر کاربردها
گرافهای دوبخشی به طور گستردهای در نظریهٔ کدگذاری مدرن مورد استفاده قرار میگیرند، مخصوصاً برای رمزگشایی کدهای (codewords) دریافتشده از کانال. گرافهای Factor و گرافهای Tanner مثالهایی از این مورد هستند. گراف Tanner، یک گراف دوبخشی است که در آن راسهای یکی از دو بخش نشاندهندهٔ ارقام یک کلمه از کد (codeword) هستند و راسهای بخش دیگر ترکیبهایی از ارقام را نشان میدهند که انتظار میرود در کد (codeword) بدون خطا مجموع آنها صفر شود.
در علوم کامپیوتر، شبکهٔ Petri net) Petri) یک ابزار مدلسازی ریاضی است که در آنالیز و شبیهسازی سیستمهای همزمان استفاده میشود. یک سیستم به صورت یک گراف دوبخشی جهتدار با دو بخش مدلسازی میشود: یک بخش از راسهای «مکان» که شامل منابع هستند و یک بخش از راسهای «رخداد» که منابع را مصرف و/یا تولید میکنند. محدودیتهای بیشتری روی راسها و یالها وجود دارند که رفتار سیستم را محدود میکنند. شبکهٔ Petri از ویژگیهای گرافهای دوبخشی جهتدار و سایر ویژگیها استفاده میکند تا امکان ارائهٔ اثباتهای ریاضی برای رفتار سیستمها و در عین حال پیادهسازی سادهٔ شبیهسازیهای سیستمها را فراهم کند.
در هندسهٔ تصویری، گرافهای Levi نوعی گراف دوبخشی هستند که برای مدلسازی واقع شدن نقاط و خطها برهم در یک پیکره (configuration) از آنها استفاده میشود. بنابر ویژگی هندسی خطوط و نقاط که هر دو خط حداکثر در یک نقطه یکدیگر را قطع میکنند و هر دو نقطه را فقط با یک خط میتوان به هم متصل کرد، گرافهای Levi شامل هیچ دوری به طول ۴ نیستند، پس طول کوتاهترین دور آنها باید ۶ یا بیشتر باشد.