ابرگراف
در ریاضیات اَبَرگراف تعمیمی از گراف است که برخلاف گرافهای عادی هر یال در آن، که به آن اَبریال میگویند، میتواند شامل تعداد دلخواهی از رأسها باشد و چندین رأس را به هم وصل کند. اَبرگراف را به صورت نشان میدهند که مجموعهای از رأسها و مجموعهای از زیرمجموعههای غیر تهی رأسها یا همان یالها میباشد.

از نیم قرن گذشته، نظریه گراف دارای اهمیت بسیاری در زمینههای مختلف از جمله هندسه، نظریه اعداد، بهینهسازی، توپولوژی، جبرهای میانی و نظیر آنها بودهاست. برای حل مسایل ترکیبیاتی جدید، لازم بود که مفهوم گراف توسعه داده شود. حدود سال١٩۶٠مفهوم ابرگراف پدیدار شد و یکی از اهداف ابتدایی آن، تعمیم برخی از نتایج کلاسیک نظریه گراف بود. نظریه ابرگراف، ابزاری مفید برای مسایل بهینهسازی گسسته است.
تعریف
اگر یک مجموعه متناهی و (به قسمی که i Є I) یک خانواده از زیرمجموعههای X باشند ، را یک ابرگراف مینامند اگر اجتماع تمامی های ناتهی برابر X شود.
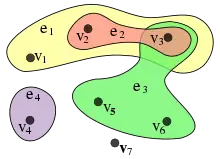
و و ... و را رأسها و و و ... و را اَبریالهای اَبرگراف است.
را مرتبهی ابرگراف و مجموع ها اندازهی ابرگراف می نامند.
تعداد ابریالهایی که رأس در آن قرار دارد درجه رأس گویند و با نمایش میدهند.
اندازه بزرگترین ابریال در هر ابرگراف را رتبه ابرگراف گویند و با نمایش میدهند.
دو رأس را مجاور گویند هرگاه ابریالی موجود باشد که شامل هر دو رأس باشد.
دو ابریال را مجزا گویند هرگاه اشتراکشان تهی باشد.
نمایش
در حالت خاص اگر فرض کنیم در مجموعه ها رابطهٔ ترتیبی وجود داشته باشد را یک گره را یک یال بین دو رأس و را به وسیلهٔ منحنی بستهای که تمام رأسهای را دربر دارد نشان می دهند.
برای نمایش ابرگرافها از ماتریس تداخل استفاده میشود به این صورت که سطرها مشخصکننده رأسها و ستونها مشخصکننده ابریالهای ابرگراف هستند، هر درایه از ماتریس برابر یک هست اگر راس i در ابریال j وجود داشته باشد.
ابرگراف k-یکنواخت
ابرگراف H را k-یکنواخت گویند هرگاه همه ابریالهای آن دقیقاً دارای K عضو باشد.
منابع
- "Results in Extremal Graph and Hypergraph Theory".
- Hypergraphes. Combinatoires des ensembles finis (Hypergraphs. Combinatorial finite sets), Gauthier-Villars, 1987, trans. English
- Graphes et Hypergraphes, in 1969 and 1970, trans. in English, Japanese. English translation: Graphs and Hypergraphs, North-Holland Publishing Company, 1973.
| مجموعهای از گفتاوردهای مربوط به گراف در ویکیگفتاورد موجود است. |