گره سلطه گر

در گراف های جهت دار، زمانی می‌گوییم گره ${\displaystyle w}$ بر گره ${\displaystyle v}$ غلبه می‌کند که به ازای هر گره ${\displaystyle n}$ همه مسیر ها از ${\displaystyle n}$ به ${\displaystyle v}$، از گره ${\displaystyle w}$ عبور کند. در نتیجه می‌توان گفت هر گره بر خودش غلبه می‌کند. با توجه به تعریف می‌توان برای هر گره مجموعه‌ای از گره های سلطه گر در نظر گرفت که بر این گره غلبه می‌کنند. همچنین می‌توان برای هر گراف یک درخت سلطه گر تعریف کرد که به ازای هر گره در گراف، اجداد این گره در درخت، گره های سلطه گر بر این گره در گراف هستند.

• گره ${\displaystyle v}$ بر گره ${\displaystyle w}$ اکیداً غلبه می‌کند زمانی که گره ${\displaystyle v}$ بر گره ${\displaystyle w}$ غلبه کرده و ${\displaystyle v\neq w}$ باشد.
• گره‌های سلطه گر آنی گره ${\displaystyle v}$ به مجموعه گره‌هایی می گویند که فقط بر گره ${\displaystyle v}$ به صورت اکید غلبه کرده و بر هیچ گره دیگری اکیداً غلبه نکند[1].
• گره‌های سلطه گر مرزی گره ${\displaystyle v}$ به مجموعه گره‌هایی می‌گویند که گره ${\displaystyle v}$ بر والدهای مستقیم آنها غلبه کرده ولی به صورت اکید بر آن گره‌ها غلبه نکند.

درخت سلطه‌گر حاصل از گراف موجود در تصویر.

در این گراف جهت دار با توجه به شکل می‌توان دید که گره ۱ بر تمام گره‌ها غلبه می‌کند. گره ۲ بر تمام گره ها به جز گره ۱ غلبه می‌کند و دیگر گره‌ها در گراف فقط بر خود غلبه می‌کنند. همچنین گره ۱برای گره ۲ یک گره سلطه گر آنی محسوب می‌شود و گره ۲ نیز برای گره های ۳، ۴، ۵ و ۶ گره سلطه گر آنی بوده.

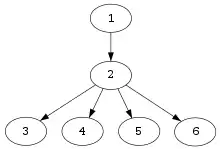
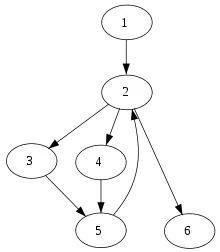
بنابر تعریف می‌توان برای سلطه گری اکید نتیجه گرفت که نزدیک گره سلطه گر اکید برای هر گره یکتا بوده و یک گره برای آن وجود دارد.

تاریخچه و کاربرد

تعریف گره سلطه گر یا غالب برای اولین بار توسط ریس پروسر در مقاله‌ای تحت عنوان کاربردهای ماتریس بولی برای تحلیل نمودارهای جریان[2] ارائه شد. او در این مقاله الگوریتمی برای پیدا کردن گره های سلطه گر ارائه نکرد و صرفاً آن را تعریف کرده. اولین الگوریتم برای این مساله ده سال بعد توسط ادوارد لوری و مدلاک ارائه شد[3]. از کاربرد های آن می‌توان به زمینه های بهینه سازی برنامه، تولید کد، تست مدار اشاره کرد. همچنین در کامپایلر ها از اطلاعات حاصل از سلطه گری گره‌ها استفاده زیادی می‌شود. برای مثال یک کاربرد آن در کامپایلر برای پیدا کردن حلقه ها در بهینه سازی کد به کمک بلوک های پایه است[4].

الگوریتم پیدا کردن گره‌های سلطه گر

با توجه به تعریف برای هر گره ${\displaystyle n}$ اگر ${\displaystyle {\text{Dom}}(n)}$ برابر با مجموعه گره‌های سلطه گر بر گره ${\displaystyle n}$ در نظر بگیریم آنگاه رابطه زیر را خواهیم داشت.

$${\displaystyle {\text{Dom}}(n)=(\bigcap _{p\in preds(n)}{\text{Dom}}(p))\ \cup \ \{n\}}$$

در اینجا ${\displaystyle preds(n)}$ برابر است با مجموعه تمام گره‌هایی که وارد گره ${\displaystyle n}$ می‌شوند یعنی یک یال از سمت آنها به ${\displaystyle n}$ وجود دارد. همچنین برای گره شروع در گراف داریم

$${\displaystyle {\text{Dom}}(n_{0})=\{n_{0}\}}$$

با داشتن این اطلاعات برای پیدا کردن گره‌های سلطه گر هر گره در گراف می‌توان الگوریتم زیر را پیاده سازی کرد.

// n0 : start node
for n in graph - {n0}:
    Dom[n] = graph

changed = True
while changed:
    changed = False
    for n in graph:
        new = []
        for p in preds(n):
            new = intersection(new, Dom[p])
        new = new + [n]
        if new != dom[n]:
            dom[n] = new
            changed = True

این الگوریتم در زمان اجرای ${\displaystyle O(n^{2})}$ تمام مجموعه های سلطه گر را می‌یابد که می‌توان با استفاده از داده ساختار های خاص زمان اجرا را بهتر کرد[5]. الگوریتم دیگری توسط رابرت تارجان و توماس لینگوار ارائه شده که به وسیله الگوریتم جستجوی اول عمق (الگوریتم dfs) در زمان تقریباً خطی این کار را انجام می‌دهد[1].

الگوریتم پیدا کردن گره‌های سلطه گر مرزی

با توجه به تعریف برای گره سلطه گر مرزی می‌توان رابطه های زیر را بدست آورد.

$${\displaystyle {\text{DF}}(v)={\text{SUCC}}(DOM^{-1}(v))-{\text{DOM!}}^{-1}(v)}$$

که در اینجا ${\displaystyle {\text{DF}}(v)}$ همان مجموعه گره‌های سلطه گر مرزی ${\displaystyle v}$ است و ${\displaystyle {\text{DOM}}^{-1}(v)}$ برابر مجموعه گره‌هایی است که ${\displaystyle v}$ بر آن‌ها غلبه می‌کند و ${\displaystyle {\text{DOM!}}^{-1}(v)}$ برابر است با ${\displaystyle {\text{DOM!}}^{-1}(v)-\{v\}}$. همچنین برای ${\displaystyle {\text{SUCC}}(S)}$ که ${\displaystyle S}$ یک مجموعه است داریم ${\displaystyle {\text{SUCC}}(S)=\bigcup _{s\in S}{\text{SUCC}}(s)}$ که اینجا ${\displaystyle {\text{SUCC}}}$ برای گره ${\displaystyle s}$ برابر است مجموعه تمام گره هایی که از ${\displaystyle s}$ به آنها در گراف جهت دار مسیر وجود دارد. با این رابطه ها می‌توان رابطه زیر را بدست آورد.

$${\displaystyle {\text{DF}}(v)={\text{DF}}_{local}(v)\cup (\bigcup _{w\in Children(v)}{\text{DF}}_{up}(w))}$$

که در اینجا ${\displaystyle Children(v)}$ فرزندان ${\displaystyle v}$ در درخت سلطه گر اند. ${\displaystyle {\text{DF}}_{local}(v)}$ برابر است با تمام ${\displaystyle {\text{SUCC}}(v)}$ که ${\displaystyle v}$ بر آنها را به صورت اکید غلبه نمی‌کند. ${\displaystyle {\text{DF}}_{up}(w)}$ زیر مجموعه‌ای از ${\displaystyle {\text{DF}}(w)}$ است که ${\displaystyle v}$ بر آنها به صورت اکید غلبه نمی‌کند. با توجه به این رابطه الگوریتم زیر بدست می‌آید[6].

def FindDF(v):
    DF[v] = []
    for w in children(v):
        FindDF(w)
        for u in DF[w]:
            if not strictly_dom(v,u):
                DF[v].append(u)
    for w in succ(v):
        if not strictly_dom(v,w):
                DF[v].append(w)

منابع

1. LengauerThomas; Endre, TarjanRobert (1979-01-01). "A fast algorithm for finding dominators in a flowgraph". ACM Transactions on Programming Languages and Systems (TOPLAS). doi:10.1145/357062.357071.
2. "Applications of Boolean matrices to the analysis of flow diagrams | Papers presented at the December 1-3, 1959, eastern joint IRE-AIEE-ACM computer conference". dl.acm.org. doi:10.1145/1460299.1460314. Retrieved 2020-01-26.
3. S, LowryEdward; W, MedlockC (1969-01-01). "Object code optimization". Communications of the ACM. doi:10.1145/362835.362838.
4. Loukas Georgiadis, Robert E. Tarjan, Renato F. Werneck. «Finding Dominators in Practice» (PDF).
5. Keith D. Cooper, Timothy J. Harvey, and Ken Kennedy. «A Simple, Fast Dominance Algorithm» (PDF).
6. «Dominator Algorithms» (PDF).