رنگ‌آمیزی گراف

در نظریه گراف، رنگ‌آمیزی گراف یکی از حالت‌های خاص مسئله‌های برچسب‌گذاری گراف است. رویکرد کلی آن استفاده از نظیر کردن رنگهایی به یالها یا راس‌هاست که این رنگ‌آمیزی محدودیت خاصی را رعایت کند. در ساده‌ترین حالت، رنگ‌آمیزی‌ای مورد نظر است که در آن هیچ دو راس مجاوری هم رنگ نباشند (رنگ‌آمیزی راسها). علاوه بر آن رنگ‌آمیزی یالها به همین صورت تعریف می‌شود.

یک رنگ‌آمیزی گراف پترسن به کمک ۳ رنگ (کمترین تعداد رنگ ممکن).

رنگ‌آمیزی گراف کاربردهای زیادی در زمینه‌های عملی و تئوری گوناگون دارد. علاوه بر مسئله‌های کلاسیک تعریف شده در این زمینه، با در نظر گرفتن محدودیت‌های مختلفی روی نوع گرافها، روی روش رنگ‌آمیزی و حتی تعداد و رنگ عناصر گراف مسئله‌های متنوعی با کاربردهای وسیع در صنعت و علوم تعریف و حل می‌شود. با وجود اینکه این مسئله از نظر علمی هنوز در حال رشد و بررسی بیشتر می‌باشد، با ظهور جدول سودوکو در بین عموم مردم شناخته و مشهور شده‌است.

تاریخچه

یک رنگ‌آمیزی ۴ رنگه نقشه ایالات متحده (بدون در نظر گرفتن آبها، کشورهای همسایه و متن نام ایالت‌ها).

اولین نتیجه‌های بدست آمده در مورد رنگ‌آمیزی گراف از تلاش‌های انجام شده بر روی گراف‌های مسطح برای حل مسئله رنگ‌آمیزی نقشه بدست آمد. در آن زمان فرانسیس گوتری ادعا کرد که رنگ‌آمیزی نقشه ایالت‌های مختلف بریتانیا روی نقشه، به‌طوری‌که هیچ دو ایالت مجاوری همرنگ نشوند، می‌تواند با ۴ رنگ انجام شود (شرط کافی). برادر گوتری این مسئله را برای معلم ریاضی خود آگوستوس دو مورگان، در کالج دانشگاهی فرستاد. دو مورگان، این مسئله را در سال ۱۸۵۲ میلادی در نامه‌ای که به ویلیام همیلتون نوشت مطرح کرد. در سال ۱۸۷۹ آرتور کیلی این مسئله را در انجمن ریاضی شهر لندن مطرح کرد. در همان سال آلفرد کمپ، نتایج بدست آمده را منتشر کرد و برای یک دهه تصور می‌شد این مسئله حل‌شده‌است. برای تلاش‌های کمپ در این زمینه او به عنوان یکی از اعضای جامعه سلطنتی و بعدها به عنوان ریاست انجمن ریاضی شهر لندن انتخاب شد.

در سال1890 Heawood، ادعا کرد که استدلال کمپ اشتباه بوده‌است و اثبات این مسئله را برای ۵ رنگ منتشر کرد. در قرن معاصر او تلاش‌های زیادی برای اثبات روش‌های رنگ‌آمیزی نقشه با تعداد ۴ رنگ صورت گرفت که در نهایت در سال ۱۹۷۶ توسط Kenneth Appel وWolfgang Haken این مسئله به کمک ایده‌های خود Heawood و کمپ انجام شد که در آن زمان به دلیل استفاده از کامپیوتر برای اثبات مسئله، شدیداً مورد قبول واقع نشد.

رنگ‌آمیزی گراف از اوایل دهه ۷۰ به عنوان یک مسئله الگوریتمی مورد بررسی قرار گرفته‌است، به‌طوری‌که جزء یکی از ۲۱ مسئله NP-Complete که Karp معرفی کرد قرار گرفته.

واژه‌ها و اصطلاحات

این گراف به ۱۲ روش می‌تواند رنگ‌آمیزی ۳ رنگه شود.

رنگ‌آمیزی راسی

معمولاً تا زمانی که ذکر نشده‌است، منظور از رنگ‌آمیزی گراف یک رنگ‌آمیزی مناسب رأس‌های یک گراف است. یا به عبارتی یک برچسب‌گذاری رأس‌های گراف است به شکلی که هیچ دو راسی که یک یال آن‌ها را متصل می‌کنند همرنگ نباشند. از آنجایی که یک طوقه نمی‌تواند این ویژگی را داشته باشد، این گراف‌ها باید بدون طوقه باشند.

استفاده از رنگ‌ها برای این رنگ‌آمیزی گراف به استفاده آن‌ها در رنگ‌آمیزی نقشه بازمی‌گردد. چرا که از تعداد رنگ‌های کمی برای این منظور استفاده می‌کنیم. به‌طور طبیعی هر رنگ را متناظر یکی از اعداد طبیعی … و۳و۲و۱ در نظر می‌گیریم.

به رنگ‌آمیزی که در آن حداکثر از k رنگ استفاده می‌شود، رنگ-امیزی k تایی گفته می‌شود. به کوچکترین عددی که می‌توان رأس‌های یک گراف را رنگ‌آمیزی کرد را با (X)G نشان می‌دهیم. گرافی که می‌توان آن را با یک رنگ‌آمیزی k تایی رنگ کرد، گراف k رنگ شونده نامیده می‌شود. مجموعه‌ای از رأس‌های یک گراف که همرنگ رنگ شده‌اند یک کلاس رنگی را تشکیل می‌دهند. هر کلاس رنگی یک مجموعه مستقل را تشکیل می‌دهد.

تمامی گراف‌های غیرایزومرفیک از درجه ۳ و تعداد روش‌های رنگ‌آمیزی آنها.

چندجمله‌ای رنگی

چندجمله‌ای‌های رنگی به تعداد روش‌های رنگ‌آمیزی یک گراف اطلاق می‌شود که تعداد رنگ‌های مورد استفاده از تعداد مشخصی بیشتر نشود. برای مثال گراف شکل سمت چپ با ۱۲ روش با ۳ رنگ، رنگ‌آمیزی می‌شود. رنگ‌آمیزی آن با ۲ رنگ غیرممکن است. با ۴ رنگ این کار را می‌توان با ۷۲ = ۴٫۱۲ + ۲۴ روش رنگ کرد (اگر حتماً از هر ۴ رنگ استفاده کنیم ۲۴ = !۴ روش ممکن است). برای گراف فوق جدول تعداد حالت‌های ممکن به صورت زیر خواهد بود.

تعداد رنگ‌ها	۱	۲	۳	۴	…
تعداد حالت‌های رنگ‌آمیزی	۰	۰	۱۲	۷۲	…

چندجمله‌ای رنگی تابعی است به صورت (P(G, t که تعداد حالت‌های رنگ‌آمیزی t-تایی گراف G را می‌شمارد. همان‌طور که از اسم ان مشخص است این تعداد یک چندجمله‌ای است که برای مثال فوق

(P(G, t) = t(t − 1)2(t − ۲

پس برای این گراف P(G، ۴) = ۷۲ روش خواهیم داشت.

به توابع چندجمله‌ای رنگی برای گراف‌های خاص زیر توجه کنید:

چندجمله‌ای رنگی برای گراف‌های خاص

مثلثی K3	${\displaystyle t(t-1)(t-2)}$
گراف کامل Kn	${\displaystyle t(t-1)(t-2)\cdots (t-(n-1))}$
درخت با n راس	${\displaystyle t(t-1)^{n-1}}$
گراف مسیر pn	${\displaystyle t(t-1)^{n-1}}$
گراف دوری Cn	${\displaystyle (t-1)^{n}+(-1)^{n}(t-1)}$
گراف پترسن	${\displaystyle t(t-1)(t-2)(t^{7}-12t^{6}+67t^{5}-230t^{4}+529t^{3}-814t^{2}+775t-352)}$

رنگ‌آمیزی یالی

رنگ‌آمیزی یالی یک گراف به نوعی از رنگ‌آمیزی گراف اطلاق می‌شود که در آن یال‌ها طوری رنگ می‌شوند که هیج راسی وجود نداشته باشد که مرتبط با ۲ یال همرنگ باشد. یک رنگ‌آمیزی یال‌های یک گراف با k رنگ یک رنگ‌آمیزی یالی k-رنگی نام دارد که برابر با تعداد تعداد حالت‌های تطابق تایی متناظر می‌باشد.

کاربردها

مسئله چندجمله ای‌های فامی

در شرکت شیمیایی J&J، جین متصدی انبار کردن ترکیب‌های شیمیایی در انبار شرکت است. چون بعضی از انواع ترکیب‌ها (نظیر اسید و بازها) نباید در مجاورت هم نگهداری شوند، تصمیم می‌گیرد که از همکارش جان بخواهد که انبار را به ناحیه‌های جدا از هم ذخیره‌سازی تقسیم کند که بتوان مواد شیمیایی ناسازگار با هم را در بخش‌های جدا از یکدیگر انبار کرد. چطور می‌تواند تعداد بخش‌های ذخیره‌سازی را که همکارش باید بسازد معین کند؟ اگر شرکتی ۲۵ ترکیب شیمیایی بفروشد، فرض کنیدc₁، c₂، …، c₂₅=v مجموعهٔ رأس‌ها باشد. به ازای ۱≤i≤y≤۲۵ یالc_i، c_jرا، اگر ضروری است که c_i و c_j در بخش‌های جدا از هم انبار شوند، رسم می‌کنیم. این عمل، گراف بی سوی (G=(V,E را به ما می‌دهد. اینک مفهوم زیر را معرفی می‌کنیم.

تعریف: اگر(G=(V,E گرافی بی سو باشد، یک رنگ آمیزی خاص G وقتی صورت می‌گیرد که رأس‌های G را به قسمی رنگ زنیم که اگر a , b یالی از G باشد، آن گاه a و b رنگ‌های مختلف داشته باشند. (بنابراین رأس‌های مجاور رنگ‌های مختلف دارند) مینیمم تعداد رنگ‌های لازم برای رنگ کردن G را عدد فامی G می‌نامند و با(χ(G نشان می‌دهند. اگر به یاری جین دربارهٔ مشکل انبار برگردیم، متوجه می‌شویم که تعداد بخش‌های ذخیره‌سازی که جان باید بسازد برابر با (χ(G ی گرافی است که با c₁، c₂، …، c₂₅=vساختیم. امّا چگونه (χ(G را حساب کنیم؟ قبل از انجام هرکاری دربارهٔ چگونگی تعیین عدد فامی گراف، به مطلب وابستهٔ زیر توجه می‌کنیم.

حدود ۱۸۵۰، فرانسیس گاتری (۱۸۳۱–۱۸۹۹) بعد از نشان دادن چگونگی رنگ آمیزی استان‌های نقشهٔ انگلیس تنها با چهار رنگ، به مسئلهٔ کلی علاقه‌مند شد. اندکی بعد از آن، «مسئله چهار رنگ» را به برادر کوچکش فردریک نشان داد. در آن زمان فردریک گاتری (۱۸۳۳–۱۸۶۶) دانشجوی اوگاستس دمورگن (۱۸۰۶–۱۸۷۱) بود که مسئله را (در ۱۸۵۲) با ویلیام همیلتن (۱۸۰۵–۱۸۶۵) در میان گذاشت. این مسئله مورد توجه همیلتن قرار نگرفت و حدود ۲۵ سال مسکوت ماند. بعداً در ۱۸۷۸، جامعهٔ علمی از طریق اطلاعیهٔ آرثر کیلی (۱۸۲۱–۱۸۹۵) در گردهمایی انجمن ریاضی لندن از مسئله آگاه شد. کیلی در ۱۸۷۹ مسئله را در اولین مجلهٔ گزارش انجمن سلطنتی جغرافیا بیان کرد. مدت کوتاهی بعد از آن، سرآلفرد کمپ (۱۸۴۹–۱۹۲۲)، ریاضیدان انگلیسی، برهانی پیدا کرد که بیش از یک دهه غیرقابل تردید باقی‌ماند. بعداً در ۱۸۹۰ پرسی جان هیوود (۱۸۶۱–۱۹۵۵)، ریاضیدان دیگر انگلیسی در کار کمپ خطایی یافت. مسئله تا سال ۱۹۷۶ حل نشده ماند، تا اینکه سرانجام کنت آپل و ولفگانک هیکن آن را حل کردند. در برهان آن‌ها تحلیل کامپیوتری بسیار پیچیده‌ای از پیکر بندی‌های (کاهش پذیر) ۱۹۳۶ به کار رفته‌است.

گر چه تنها چهار رنگ برای رنگ آمیزی خاص ناحیه‌های یک نقشهٔ هامنی مورد نیاز است، ولی برای رنگ آمیزی خاص رأس‌های گراف‌های غیر هامنی بیش از چهار رنگ لازم است. با چند مثال کوچک شروع می‌کنیم. در این صورت راهی برای تعیین (χ(Gاز زیر گراف‌های کوچکتر G خواهیم یافت. آنچه را که چندجمله‌ای فامی G می‌نامند نیز به دست خواهیم آورد و چگونگی استفاده از آن را در محاسبه (χ(G خواهیم دید.

مثال ۱: برای گراف G در شکل ۱، از رأس a شروع می‌کنیم و سپس در هر رأس، عدد فامی لازم برای رنگ آمیزی رأس‌های G را که برای آن‌ها در نظر گرفته‌ایم می‌نویسیم. وقتی به رأس b می‌رویم، عدد ۲ نیاز ما به رنگ دوم است و اگر به صورت الفبایی تا f پیش برویم متوجه می‌شویم که برای رنگ آمیزی خاص a,b،c,d،e,f به دو رنگ نیاز داریم. برای رأُس g، رنگ سومی لازم است؛ این رنگ سوم را می‌توان برای رأس h هم به کار برد، زیرا g , h یالی از G نیست. پس χ(G)=۳.

مثال ۲: الف) برای هر χ(K _n )=n ,n≥۱.

ب) عدد فامی گراف شکل ۲ (هرشل) برابر ۲ است.

ج) اگر G گراف پترسن باشد آن گاه χ(G)=۳.

مثال ۳: فرض کنید G گرافی است که در شکل ۳ نشان داده‌ایم. برای U=b,f،h,i، زیر گراف القایی (U) از G، با K₄ یکریخت است، به قسمی که(χ(G)≥χ(K₄. بنابراین، اگر بتوانیم راهی برای رنگ آمیزی خاص رأسهای G با چهار رنگ تعیین کنیم، آن گاه می‌دانیم که χ(G)=۴. یک راه انجام این کار، این است که رأس‌های e ,f، g را با رنگ آبی، رأس‌های b و j را با رنگ‌های قرمز، رأس‌های c و h را با رنگ سفید و رأسهای a , d، i را با رنگ سبز رنگ بزنیم.

اینک به روشی برای تعیین (χ(G برمی گردیم. آنچه مطرح می‌کنیم از بسط مقالهٔ تحقیقی [۲۲]، اثر رید گرفته شده‌است.

فرض کنید G گرافی بی سو ست و λ عدد صحیح مثبت معرّف تعداد رنگ‌های است که برای رنگ آمیزی خاص رأس‌های G موجودند. هدف ما یافتن چندجمله‌ای (P(G، λ برحسب متغیر λ است که بیان می‌کند به چند راه مختلف رأس‌های G را، با استفاده از حداکثر λ رنگ، رنگ کنیم. در سراسر این بحث، رأس‌های گراف بی سوی (G=(V,E به وسیله برچسب‌ها از هم متمایزند. در نتیجه دو رنگ آمیزی خاص چنین گرافی به مفهوم زیر متمایز در نطر گرفته می‌شوند: رنگ آمیزی خاص (رأس‌های G) که حداکثر λ رنگ به کار می‌برد تابعی مانند f با حوزهٔ V و حوزهٔ تمام ۳٬۲٬۱، …، λ است، که در آن، برای رأس‌های مجاور f(u)≠f(v),u،v∈V. لذا تفاوت رنگ آمیزی خاص از متفاوت بودن این تابع‌ها معلوم می‌شود.

مثال ۴: الف) اگر (G=(V,E با V|=n|و E=∅، آن گاه G عبارت از n نقطهٔ تنهاست، و بنابر اصل ضرب P(G، λ)=λⁿ.

ب) اگر G=K_n، آن گاه حداقل باید n رنگ موجود باشد تا G را به‌طور خاص رنگ بزنیم. در اینجا، بنابر اصل ضرب، (P(G، λ)=λ(λ-۱)(λ-۲)…(λ-n+1، که آن را با λ⁽ⁿ نشان می‌دهیم. به ازای P(G، λ)=۰، λ<n و راهی برای رنگ آمیزی خاص K_n وجود ندارد. وقتی (λ=n=χ(G، برای اولین بار P(G، λ)>۰

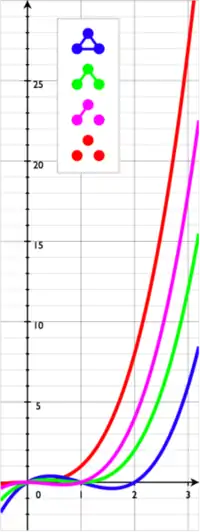
ج) برای هر مسیر در شکل ۴ تعداد انتخاب‌ها در هر رأس متوالی را در نظر می‌گیریم. اگر به صورت الفبایی پیش برویم، در میابیم که P(G₁، λ)=λ(λ-1)³ و P(G₂، λ)=λ(λ-1)⁴. چون (P(G₁،۱)=۰=P(G₂،۱، ولی (χ(G₁)=χ(G₂)=۲، P(G₁،۲)=۲=P(G₂،۲، اگر پنج رنگ موجود باشند، می‌توانیم به‌طور خاص G₁ را به۳۲۰ راه رنگ بزنیم؛ G₂ را نیز می‌توان به همین طریق به۱۲۸۰ راه رنگ کرد.

(به‌طور کلی :اگر G مسیری با n رأس باشد، آن گاهP(G، λ)=λ(λ-1)^n-1)

د) اگر G از مؤلفه‌های C₁،C₂، …،C_k ساخته شده باشد، آن گاه باز بنابر اصل ضرب، نتیجه می‌شود که (P(G، λ)=P(C₁، λ).P(C₂، λ)…P(C_k، λ.

به عنوان نتیجه‌ای از مثال ۴ (د) توجه خود را بر گراف‌های همبند متمرکز می‌کنیم. در بسیاری از موارد در ریاضیات گسسته، برای حلّ مسائل با حالت‌های زیاد روش‌هایی که به کار رفته‌اند، تفکیک این حالت‌ها به دو یا چند حالت کمتر است. ما نیز همین روش را برای حل مسئله به کار می‌بریم. برای انجام این کار به مفاهیم و نمادگذاری زیر نیاز داریم. فرض کنید(G=(V,E گرافی بی سو باشد. برای e=a,b ∈E فرض می‌کنیم G_e معرف زیر گراف G حاصل از حذف e از G، بدون برداشتن رأس‌های a و b است؛ یعنی به صورت G_e=G-e می‌باشد. از G_e، زیرا گراف دوّمی از G با اتصال رأس‌های a و b به دست می‌آید. این زیر گراف دوم را با ^'G_e نشان می‌دهیم.

مثال ۵: شکل۵، G_e و^'G_e را برای گراف G با یالی که با e مشخص شده‌است نشان می‌دهد. توجه کنید که چگونه اتصال a و b در ^'G_e از اتصال دو جفت از یال‌های d,b، d,a، a,c، b,c نتیجه می‌شود.

با استفاده از این زیر گراف‌های خاص، اینک به قضیهٔ اصلی می‌رسیم:

قضیه ۱ (قضیهٔ تجزیه برای چندجمله‌ای‌های فامی): اگر(G=(V,E گرافی همبند باشد و e∈E، آن گاه: (P(G_e، λ)=P(G، λ)+P(^'G_e، λ

برهان: فرض کنید e=a,b. تعداد راه‌های رنگ آمیزی خاص رأسهای G_e با (حداکثر) λ رنگ برابر(P(G_e، λ است. آن رنگ آمیزیهایی که در آن‌ها a و b دارای رنگ‌های متفاوت اند رنگ آمیزی‌های خاص G هستند. آن رنگ آمیزیهای G_e که رنگ آمیزیهای خاص G نیستند. وقتی رخ می‌دهند که a و b یک رنگ داشته باشند. امّا هر یک از این رنگ آمیزی‌ها متناظر با یک رنگ آمیزی خاص برای ^'G_e است. این افراز(P(G_e، λ رنگ آمیزی به دو زیر مجموعهٔ مجزای مشخص شده، از معادلهٔ (P(G_e، λ)=P(G، λ)+P(^'G_e، λ نتیجه می‌شود.

مثال ۶: محاسبات زیر ،(P(G، λ را برای G که دوری به درازای ۴ است ،(شکل۶) به دست می‌دهد.

از مثال ۲ (ج) ،P(G_e، λ)=λ(λ-1)³. با G_e '= K₃ داریم P(^'G_e، λ)=λ⁽³. بنابراین P(G، λ) = λ(λ-1)³-λ(λ-۱)(λ-۲) = λ(λ-۱)[(λ-1)²-(λ-۲)] = λ(λ-۱)[λ²-3λ+۳]=λ⁴-4λ³+6λ²-3λ

چون P(G،۱)=۰ در حالی که P(G،۲)=۲>۰، داریم χ(G)=۲.

قضیه ۲: برای هر گراف G، جملهٔ ثابت در(P(G، λ برابر ۰ است.

برهان: برای هر گراف G، χ(G)>0، زیرا V≠ ∅. اگر تعداد(P(G، λ دارای جملهٔ ثابت a باشد، آن گاه P(G،۰)=a≠۰. این مطلب نتیجه می‌دهد که تعداد a راه برای رنگ کردن خاص G با ۰ رنگ وجود دارد.

قضیه ۳: فرض کنید(G=(V,E با E|>0|. در این صورت مجموع ضریب‌ها در(P(G، λ برابر با ۰ است.

برهان: چون E|≥۱|، پس χ(G)≥۲. در نتیجه P(G،۱)=۰ برابر مجموع ضریب‌ها در(P(G، λ است.

منابع

Cormen, T. H. ; Leiserson, C. E. ; Rivest, R. L. (1990), Introduction to Algorithms (1st ed.), The MIT Press