گراف پترسن

در نظریه گراف ، گراف پترسن گرافی غیر جهت دار، با ۱۰ راس و ۱۵ یال است. این گراف، گرافی کوچک می‌باشد که به عنوان مثالی مفید و همچنین مثال نقض در بسیاری از مسائل نظریه گراف به کار می‌رود.
یولیوس پترسن[1](۱۸۳۹-۱۹۱۰) دانشمندی دانمارکی بود که در سال ۱۸۹۸ گرافی را، که به نام خودش ثبت شد، به عنوان کوچکترین گراف مکعبی (گرافی که هر راس آن از درجه ۳ باشد.) بدون پل ساخت. در واقع این گراف مثال نقضی برای این ادعا بود که یک گراف مکعبی بدون پل متصل، داری یک رنگ آمیزی یالی با ۳ رنگ است. در حالی که این گراف دارای این رنگ آمیزی با ۴ رنگ می‌باشد. با این که این گراف به‌طور عمومی به یولیوس پترسن نسبت داده می‌شود، ولی درحقیقت برای اولین بار ۱۲ سال زودتر از ساختن آن توسط وی، در سال ۱۸۸۶ به وجود آمده بود.
دونالد نوث[2] اذعان می‌کند که گراف پترسن، شکل و پیکری قابل توجه‌است که به عنوان مثالی نقض برای بسیاری از اسناد و اثبات‌های خوش بینانه دربارهٔ این که چه چیزهایی ممکن است به‌طور عمومی برای گراف‌ها درست باشد، به کار می‌رود.

یولیوس پترسن

ساختار
گراف پترسن به شکل پنج ضلعی منتظم
دارای ۵ تقاطع

گراف پترسن، گراف مکمل برای گراف خط، K۵ است. همچنین گراف نسر KG۵٬۲ هم می‌باشد. این بدان معنا است که اگر برای هر کدام از زیرمجموعه‌های دو عضوی یک مجموعهٔ ۵ عضوی یک رأس در نظر بگیریم و بین هر دو رأسی که زیرمجموعه‌های نظیرشان ناسازگار باشند یک یال وصل کنیم، گراف پترسن ساخته می‌شود.
گراف پترسن، گرافی غیر مسطح است. هر گراف غیر مسطح با گراف کامل K۵ یا گراف دو بخشی کامل K۳٬۳ هم ریخت یا هومئومورف است. حال آن که پترسن با هر دو گراف هم ریخت می‌باشد.





خواص عمومی
شکل (2)
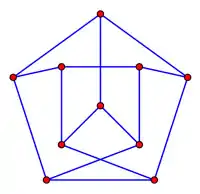
گراف پترسن با عدد تقاطع 2 . اید گراف دارای خوشه به اندازه ی دو و مجموعه ی مستقل به اندازه ی 3 است .
شکل (3)
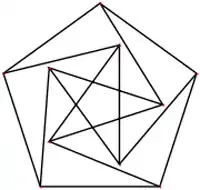
گراف پترسن با یال‌هایی برابر با واحد


دقیقاً ۱۹ گراف مکعبی متصل با ۱۰ یال وجود دارد. گراف پترسن یکی از همین ۱۹ گراف می‌باشد. این گراف تنها گرافی با ۱۰ یال از این دسته‌است که دارای قطر برابر ۲ و تنها گراف بدون پل با اندیس رنگی ۴ می‌باشد. و نهایتاً تنها گراف بدون پل با ۱۰ یال است که همیلتنی نیست.
متداول‌ترین و متقارن‌ترین شکل گراف پترسن که یک پنج ضلعی با یک ستارهٔ پنج رأس درون آن است که هر یک از رأس‌هایش به رأس‌های پنج ضلعی با یک یال وصل می‌شود، دارای ۵ نقطه تقاطع می‌باشد(شکل(۱)).این روش ترسیم بهترین روش برای کمینه کردن تعداد تقاطع‌ها نیست. روشی دیگر برای کشیدن گراف پترسن با دو نقطهٔ تقاطع وجود دارد.(شکل(۲)) بنابراین عدد تقاطع گراف پترسن ۲ است.
همچنین گراف پترسن می‌تواند به گونه‌ای رسم شود که یال‌ها دارای طول برابر واحد باشند. این نوع، یک گراف به طول واحد است.(شکل(3))














دور و مسیر همیلتونی
شکل (4)
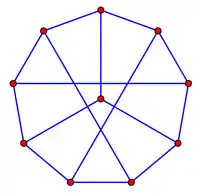
گراف پترسن به عنوان گراف شبه همیلتونی

گراف پترسن دارای مسیر همیلتونی است ولی دور همیلتونی ندارد. همچنان که در بالا ذکر شد این گراف کوچکترین گراف مکعبی بدون پل است که دور همیلتونی ندارد. در نتیجه گراف همیلتونی نیست. ولی این گراف، شبه همیلتونی است، بدان معنی که با وجود این که دور همیلتونی ندارد ولی با حذف کردن هر یال آن تبدیل به گراف همیلتونی می‌شود و ضمناً کوچترین گراف شبه همیلتونی نیز می‌باشد.(شکل(۴)) گراف پترسن یکی از ۵ گراف متصل راس-ترایا است که دور همیلتونی ندارد.








رنگ آمیزی
شکل (5)
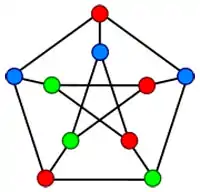
گراف پترسن با شماره رنگی 3

گراف پترسن دارای شماره رنگی ۳ است. این بدان معنا است که راس‌های آن می‌توانند با ۳ رنگ، اما نه با ۲، رنگ شوند به طوری که هیچ یالی دو راس همرنگ را متصل نکند.(شکل(۵)) همچنین دارای اندیس رنگی ۴ می‌باشد که یعنی برای رنگ کردن یال‌ها به ۴ رنگ نیاز داریم.







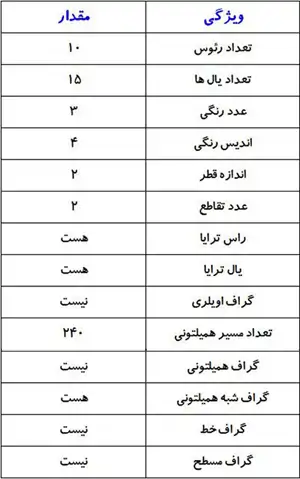
جدول خصوصیات

در جدول زیر بعضی از خواص این گراف به‌طور خلاصه آمده‌است:

پانویس
  1. Julius Petersen
  2. Donlad Knuth

منابع
در ویکی‌انبار پرونده‌هایی دربارهٔ گراف پترسن موجود است.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.