تطابق (گراف)

درنظریه گراف، به مجموعه‌ای از یال‌های گراف که با هم گره‌ای هموند ندارند، تطابق یا مجموعه‌ی ناوابسته‌ی یال‌ها گفته می‌شود. تطابق دوبخشی حالتی ویژه از پرسمان شبکه شاره است.

تعریف

در گراف داده‌شدهٔ G با مجموعهٔ یال‌ها و گره‌ها مشخص که می‌توان آن را به صورت (G(V,E نشان داد، به مجموعه‌ای از یال‌های ناهمسایه که هیج یک از دو یال آن گره هموند نداشته باشند، یک تطابق در G می‌گویند و آن را با M نشان می‌دهند.

در صورتی که گرهی در یکی از دو انتهای یکی از یال‌ها در تطابق گراف G واقع شده باشد، به آن گره منطبق شده (یا اشباع) می‌گویند. در غیر این صورت، آن گره منطبق نشده است.

تطابق ماکسیمال یکی از تطابق‌های بدست آمده برای گراف G است، با این ویژگی که اگر به آن، هر یک از یال‌هایی که در گراف G وجود دارد اما در تطابق M نیامده است را اضافه کنیم، گراف به وجود آمده خاصیت تطابق بودن خود را از دست می‌دهد؛ بنابراین چنانچه تطابق M یک زیرمجموعهٔ محض از تطابق دیگری برای گراف G نباشد، آنگاه M یک گراف تطابق ماکسیمال است. به عبارت دیگر در صورتی M می‌تواند یک تطابق ماکسیمال برای گراف G باشد که هر یال از گراف G، حداقل با یکی از یال‌های M، تقاطع ناتهی داشته باشد (منظور از تقاطع، تنها در دو سر یک یال است)

تصاویر زیر، تطابق ماکسیمال را برای ۳ گراف نشان می‌دهد (گراف تطابق بیشینه با رنگ قرمز نشان داده شده‌است).

تطابق بیشینه تطابقی است که دربردارنده‌ی بیشترین تعداد ممکن از یال‌هاست؛ بنابراین ممکن است تعداد تطابقهای بیشینه برای یک گراف، بیشتر از یکی باشد. عدد تطابق گراف G، اندازهٔ تطابق بیشینه آن گراف است که با (ν(G نشان داده می‌شود. با توجه به تعاریف بالا برای تطابق بیشینه و ماکسیمال، می‌توان نتیجه گرفت که هر تطابق بیشینه، یک تطابق ماکسیمال نیز هست، اما همهٔ تطابق‌های ماکسیمال لزوماً تطابق بیشینه نیستند.

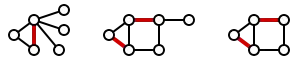
تصاویر زیر تطابق بیشینه را برای سه گراف نشان می‌دهد:

تطابق کامل تطابقی است که همهٔ گره‌های یک گراف را تطبیق می‌دهد. یعنی هر یک از گره‌ها گراف، دقیقاً با یکی از یال‌های تطابق برخورد می‌کند. در شکل‌های بالا، شکل (ب) یک تطابق کامل را نشان می‌دهد. هر تطابق کاملی، یک تطابق بیشینه و در نتیجه تطابق ماکسیمال است.

همچنین تطابق کامل، همان کوچکترین مجموعهٔ پوشش یال است. پس (ν(G) ≤ ρ(G که در آن، (ν(G سایز تطابق بیشینه است که هیچ‌گاه بیشتر از کمترین سایز برای گراف پوشش یال‌ها نیز نمی‌شود.

تطابق نزدیک به کامل به تطابقی گفته می‌شود که در آن دقیقاً یک گره، مطابقت داده نشده‌است و این تنها زمانی اتفاق می‌افتد که تعداد گره‌ها گراف فرد باشد و تطابقی که به دنبال آن هستیم، تطابق بیشینه باشد. در شکل‌های بالا، شکل (ج) یک تطابق نزدیک به کامل را نشان می‌دهد. اگر برای همهٔ گره‌ها یک گراف، یک تطابق نزدیک به کامل وجود داشته باشد که تنها همان گره را در نظر نمی‌گیرد، به آن گراف factor-critical هم گفته می‌شود.

در یک گراف تطابقی M:

• یک مسیر متناوب مسیری است که در آن، یال‌ها یک در میان یال‌های تطابقی و غیر تطابقی باشند.
• یک مسیر افزایشی مسیر متناوبی است که از یک گره آزاد (اشباع نشده) شروع و به گره آزاد دیگری ختم می‌شود.

می‌توان ثابت کرد که یک تطابق بیشینه است اگر و تنها اگر در آن مسیر افزایشی وجود نداشته باشد (این نتیجه‌گیری به قضیه برژ^*) هم مشهور است).

ویژگی‌ها

در هر گرافی که در آن گره ناهمبند وجود نداشته باشد، مجموع عدد تطابق و عدد پوشای یال، برابر تعداد گره‌ها است. چنانچه یک تطابق کامل وجود داشته باشد، عدد تطابق و عدد پوشش یال، برابر یکیدیگر و هر دو برابر V|/2| است. اگر A و B هر دو تطابق ماکسیمال باشد همواره داریم: |A| ≤ 2|B| و |B| ≤ 2|A. برای اثبات، توجه کنید که چون B تطابق است، هر یال در A می‌تواند حداکثر با دو یال در B همسایه باشد. همچنین با توجه به بیشینه بودن تطابق، هر یال در B همسایه یک یال در A است.(این استدلال را می‌توان برای گراف Aهم به کار برد و به نتایج مشابه رسید). بنابراین خواهیم داشت:

${\displaystyle |A\setminus B|\leq 2|B\setminus A|.}$

بنابراین:

${\displaystyle |A|=|A\cap B|+|A\setminus B|\leq 2|B\cap A|+2|B\setminus A|=2|B|.}$

به‌طور خاص، نامساوی بالا نشان می‌دهد که هر تطابق ماکسیمال، ۲ برابر تقریبی از تطابق بیشینه و همچنین ۲ برابر تقریبی از کوچکترین تطابق ماکسیمال است. به عنوان مثال، اگر G یک مسیر با ۳ یال و۴ گره باشد، اندازهٔ کوچکترین گراف تطابق ماکسیمال ۱ است و سایز تظابق بیشینه ۲ است.

چندجمله‌ای تطابق

تابع مولد تعداد تطابق‌های k یالی در یک گراف، چندجمله‌ای تطابق نامیده می‌شود.

فرض کنید G گرافی است که برای آن می‌خواهیم تعداد تطابق‌ها را پیدا کنیم و m_k، تعداد تطابق‌های k-یالی برای آن باشد. یکی از چندجمله‌ای‌های تطابق برای G، تابع مولد زیر است.

${\displaystyle \sum _{k\geq 0}m_{k}x^{k}.}$

تعریف دیگری، چندجمله‌ای تطابق دیگری را به صورت زیر می‌دهد:

${\displaystyle \sum _{k\geq 0}(-1)^{k}m_{k}x^{n-2k},}$

که در آن، n تعداد گره‌ها گراف است. هر یک از انواع چندجمله‌ای بالا، کاربردهای مخصوص به خود را دارد. برای کسب اطلاعات بیشتر در این مورد، می‌توانید مقالات مربوط به چندجمله‌ای‌های تطابق را مطالعه کنید.

الگوریتم‌ها و پیچیدگی رایانشی آنها

تطابق بیشینه در گراف‌های دو بخشی

اغلب اوقات مسئلهٔ تطابق برای گراف دوبخشی مطرح می‌شود. شاید پیدا کردن یک تطابق دو بخشی بیشینه (که اغلب به آن تطابق دو بخشی با سایز بیشینه گفته می‌شود) در یک گراف دو بخشی(G = (V = (X,Y),E، ساده‌ترین مسئله در قسمت تطابق باشد. الگوریتم مسیر افزایشی، در صورتی که بین هر گره مانند x ∈ X به هر گره مانند y مسیر اقزایشی وجود داشته باشد، آن را پیدا می‌کند و به تطابق اضافه می‌کند. از آنجا که هر یک از این مسیرهای افزایش می‌تواند در زمان (O(E پیدا شود، زمان اجرا برای کل این الگوریتم از مرتبهٔ (O(VE می‌شود. این راه حل معادل این است که یک منبع مانند s که به همهٔ گره‌ها در X یال دارد و همچنین یک گودال مانند t که از همهٔ گره‌ها در Y به آن یال وجود دارد، به گراف اضافه کنیم و سپس شار بیشینه را از s به t حساب کنیم. با این کار، همهٔ یال‌هایی که از X به Y جریان دارند، تطابق بیشینه را تشکیل می‌دهند.

این الگوریتم، در الگوریتم هاپ کرافت-کارپ ^*)، بهبود داده شده‌است و می‌تواند در زمان ${\displaystyle O({\sqrt {VE}})}$ اجرا شود.

راه حل دیگر برای پیدا کردن تطابق بیشینه در گراف دو بخشی، بر پایهٔ الگوریتم ضرب سریع ماتریس هاست و دارای پیچیدگی زمانی ${\displaystyle O(V^{2.376})}$ است که از نطر تئوری برای گراف‌هایی که تا حد امکان فشرده هستند، کارآمد تر است. اما در عمل این الگوریتم کندتر است. در گراف دوبخشی وزن‌دار، هر یال دارای یک وزنی است که به آن نسبت داده شده‌است. تطابق بیشینهٔ وزن‌دار برای گراف‌های دو بخشی، تطابق کاملی است که در آن مجموع مقادیر (وزن‌ها) روی یال‌های تطابق، بیشترین مقدار را داشته باشد. اگر گراف دو بخشی کامل نباشد، یال‌هایی که برای دوبخشی کامل شدن لازم است را با وزن ۰ به گراف اضافه می‌کنیم. پیدا کردن این تطابق به پرسمان انتساب مشهور است. این مسئله را می‌توان با استفاده از روش اصلاح شدهٔ یافتن کوتاه‌ترین مسیر در الگوریتم مسیر افزایشی، حل کرد. اگر از الگوریتم بلمن فورد استفاده کنیم، زمان اجرا، ${\displaystyle O(V^{2}E)}$ می‌شود. اما چنانچه از الگوریتم دیکسترا و هیپ فیبوناتچی استفاده کنیم، زمان اجرا به ${\displaystyle O(V^{2}\log {V}+VE)}$ کاهش می‌یابد. یک الگوریتم قابل توجه بلغاری، برای حل پرسمان انتساب ارائه شده‌است که از نخستین الگوریتم‌های بهینه‌سازی ترکیبی بود. راه حل اصلی این الگوریتم، نیاز به زمان اجرای ${\displaystyle O(V^{2}E)}$ دارد اما با استفاده از صف اولویت، می‌توان زمان اجرای آن را به ${\displaystyle O(V^{2}\log {V}+VE)}$ بهبود بخشید.

تطابق بیشینه

یک راه حل چندجمله‌ای برای پیدا کردن تطابق بیشینه یا تطابق با وزن بیشینه در یک گراف غیر دوبخشی وجود دارد. این روش با توجه به jack Edmonds که بنیانگذار آن بود، روش راهها، درخت‌ها و گل‌ها یا به‌طور مختصر الگوریتم Edmonds نامگذاری شد. این الگوریتم از یال‌های دو سویه استفاده می‌کند. این الگوریتم متعاقباً بهبود بخشیده شد تا در زمان O(√VE) اجرا شود که از مرتبهٔ زمان لازم برای پیدا کردن تطابق بیشینه در گراف‌های دو بخشی است. همچنین الگوریتم دیگری برای پیدا کردن تطابق ماکسیمال وجود دارد که بر پایهٔ ضرب سریع ماتریس‌هاست و به الگوریتم Mucha و Sankowski مشهور است. اجرای این الگوریتم از مرتبهٔ ${\displaystyle O(V^{2.376})}$ زمان می‌برد.

تطابق ماکسیمال

تطابق ماکسیمال را می‌توان به سادگی و با استفاده از یک الگوریتم حریصانه بدست آورد. یک تطابق بیشینه، تطابقی ماکسیمال نیز هست؛ بنابراین می‌توان بزرگ‌ترین تطابق ماکسیمال را نیز در زمان چندجمله‌ای پیدا کرد.

با این وجود هنوز هیچ الگوریتم چندجمله‌ای برای پیدا کردن کوچکترین گراف تطابق ماکسیمال که بزرگ‌ترین تطابق بیشینه با کمترین تعداد یال ممکن است، وجود ندارد.

توجه کنید که تطابق ماکسیمال با kیال، یک مجموعهٔ غالب یال‌ها^*) با k یال است. در مقابل، اگر کوچک‌ترین مجموعهٔ غالب یال‌ها با k یال را در اختیار داشته باشیم، می‌توان در زمان چندجمله‌ای تطابق ماکسیمال با k یال را ساخت؛ بنابراین پرسمان یافتن کوچکترین گراف تطابق ماکسیمال، معادل پرسمان یافتن کوچکترین مجموعهٔ غالب یال‌هاست. هر دوی این مسائل بهینه‌سازی ان‌پی-سخت است. نسخه‌های تصمیم گیری از این مسائل، از جمله مثال‌های کلاسیک مسائل ان پی (کامل) هستند. هر دوی این مسائل را می‌توان تا جملهٔ دوم در زمان چندجمله‌ای تقریب زد: پیدا کردن تطابق بیشینه دلخواه به سادگی.

پرسمان شمارش

پرسمان پیدا کردن تعداد تطابق‌های کامل برای بک گراف مسئله‌ای #پی-کامل است. هر چند که نظریهٔ قابل توجه Kasteleyn نشان می‌دهد که تعداد تطابق‌های بیشینه در یک گراف مسطح را می‌توان با استفاده از الگوریتم FKT دقیقاً در زمان چندجمله‌ای محاسبه کرد. همچنین یک تقریب تصادفی اما چندجمله‌ای برای شمارش تعداد تطابق‌های دوبخشی وجود دارد.

نطریهٔ کونیگ نشان می‌دهد که در گراف‌های دو بخشی، تطابق بیشینه از نطر اندازه برابر با کوچکترین پوشش گره است. با توجه به نتایج این نطریه، مسئلههٔ بزرگ‌ترین مجموعهٔ ناوابسته و بزرگترین پوشش گره‌ها ممکن است در زمان چندجمله‌ای برای گراف‌های دو بخشی حل شود. قضیه هال، توصیفی از گراف‌های دو بخشی که تطابق کامل دارد را فراهم می‌کند و همچنین قضیهٔ tutte این خصوصیات را برای گراف دلخواه بیان می‌کند.

منابع

• http://en.wikipedia.org/w/index.php?title=Matching_(graph_theory)&oldid=464266371)

جستارهای وابسته

• نظریه گراف
• الگوریتم حریصانه
• رنگ‌آمیزی گراف

پانویس

1. ^  Berge's lemma.
2. ^  Hopcroft-Karp algorithm
3. ^  Edge dominating set.