بیشینه صرفهجویی (تبارزایی)
بیشینه صرفهجویی یا ماکزیمم پارسیمونی (به انگلیسی: Maximum parsimony) یک روش آماری غیر پارامتری است که بهطور معمول در تبارزایش (فیلوژنتیک) محاسباتی برای تخمین سیر تبارزایی جانداران استفاده میشود. تحت فرض بیشینه صرفهجویی با دادههای موجود درخت تبارزایی بهتر است که براساس فرض به وجود آمدن کمترین تغییرات باشد.
به تفصیل
بیشینه صرفهجویی جزئی از روشهای تخمین درخت بر اساس شناسهها است که از یک ماتریس گسستهٔ خصیصههای تبارزایی برای نتیجه گرفتن یک یا چند درخت بهینه استفاه میکند. این روشها با ارزیابی کاندیداهای درخت فیلوژنتیک بر اساس یک معیار آشکار بهینهسازی کار میکنند. در نهایت درخت با بیشترین امتیاز به عنوان تخمینی از درخت بیانکنندهٔ روابط بین ردهها (taxa) شناخته میشود. بیشینه صرفهجویی با بیشتر انواع دادههای فیلوژنتیک استفاده میشود؛ و اخیراً تنها روش بر پایهٔ کاراکترها بود که بهطور گسترده برای تخمین درخت برای دادههای ریختشناسی استفاده میشد.
تخمین نژادها مسئلهٔ بدیهی ای نیست. تعداد بسیار زیادی از درختهای فیلوژنتیک ممکن، برای هر سایز قابل قبول از تاگزاها وجود دارند. به عنوان مثال، ده گونه بیشتر از دو میلیون درخت بی ریشهٔ ممکن به وجود میآورند. این احتمالات باید جستجو شوند تا درختی با بهترین حالت بهینگی یافت شود. اگرچه، دادهها بهطور خودکار به یک راه حل سادهٔ ریاضی برای مسئله منجر نمیشوند. بهطور ایدهآل، ما انتظار داریم درختی که ساخته میشود بیانگر روابط واقعی بین گرهها باشد؛ بنابراین میتوانیم بگوییم اگر دو جاندار یک شناسه مشترک داشته باشند، آنها باید بیشتر به هم نزدیک باشند نسبت به یک جاندار ثالث که چنان ویژگی مشترکی را ندارد.
متدهایی که برای تخمین درختهای فیلوژنتیکی استفاده میشوند بهطور صریح قصد حل کردن تداخل بین دادهها را دارند و این کار را با برداشتن درختی که بیشترین شایستگی را برای بیشتر دادهها دارد انجام میدهند. گاهی اوقات بهطور اشتباه فکر میکنند که یکی از پیشفرضهای درخت پارسیمنی نادر بودن همگرایی است.
دادههای شناسهای
دادههای ورودی در یک تحلیل بیشینه صرفهجویی برای محدودهای از ردهها به شکل شناسه است. هیچ تعریف قبول شدهای برای یک کاراکتر فیلوژنتیک وجود ندارد، اما بهطور عملی یک شناسه میتواند یک مشخصه، یا محوری باشد که ردهها در راستای آن با هم متفاوتند. این مشخصهها میتوانند ریختشناختی، مولکولی، ژنتیکی، فیزیولوژیکی، یا رفتاری باشند. تنها مسئلهای که در مورد شناسهها به نظر مورد اتفاق همه میرسد این است که تفاوت کاراکتری آنها باید نشانگر و منعکسکننده رابطهٔ ارث بری آنها باشد.
هر شناسهای به وضعیتهای کاراکتری گسستهای تقسیمبندی میشود، که در آنها تغییرات مشاهده شده دستهبندی شدهاند. وضعیتهای کاراکتر اغلب به صورت توصیفکنندهها فرموله میشوند، که شرایط فرعی کاراکتر را توصیف میکنند. به عنوان مثال کاراکتر رنگ چشم میتوانند حالات آبی و قهوهای را داشته باشد. کاراکترها دو یا چند حالت میتوانند داشته باشند.
کد کردن کاراکترها برای تحلیلهای فیلوژنتیکی علم دقیقی نیست، و مسائل پیچیده و قابل توجهی در این مورد وجود دارند. بهطور عمومی، تاکسونها با یک حالت امتیاز دهی میشوند اگر آنها به یکدیگر در یک مشخصه شبیه تر باشند تا نسبت به هم در حالتی مختلف. این مسئله وقتی که حالات کاراکترها بهطور واضح مشخص نشدهاست یا وقتی که آنها نتوانند تمام تغییرات در یک کاراکتر را پوشش دهند چندان مسئلهٔ سرراستی نیست. حال سؤال این است که چه طور میتوان کاراکتر ذکر شده در بالا را برای یک تاکسون مربوط به یک شخص با چشم فندقی رنگ امتیازدهی کرد؟ همانطور که در بالا اشاره شد، کد کردن شناسهها بهطور عمومی بر پایهٔ شباهت است: چشمان رنگ فندقی و سبز ممکن است با هم آبی شوند، آنها به آن رنگ شبیه ترند (روشن بودن)، و سپس آن کاراکتر میتواند به صورت روبه رو کد شود «رنگ چشم: روشن؛ تاریک». بهطور جایگزین، کاراکترهایی با حالات چندگانه نیز میتوانند موجود باشند مانند: «رنگ چشم: قهوهای؛ فندوقی؛ آبی؛ سبز»
نمونهگیری تاکسون
زمانی که برای یک آنالیز صرفهجویی (یا هر آنالیز فیلوژنتیکی دیگر) نیاز است به تعداد تاکسونها (و کاراکترهای) موجود در آنالیز بستگی دارد. بعلاوه، چون تاکسون بیشتر به معنی این است که شاخههای بیشتری باید تخمین زده شوند، عدم قطعیت بیشتری در آنالیزهای بزرگ انتظار میرود. زیرا مجموعهٔ دادهها که موجب صرف زمان وپول میشوند اغلب بهطور مستقیم با تعداد تاکسونها مقیاس میشوند، بیشتر تحلیلها تنها تعدادی از تاکسونها که قابل نمونهگیری اند را در بر میگیرند. در حقیقت، بعضی از نویسندهها راضی شدهاند که چهار تاکسون (کمترین تعداد تاکسون برای ساخت یک درخت بدون ریشهٔ با معنی) تمام چیزی هستند که برای یک آنالیز دقیق فیلوژنتیکی لازم اند؛ و اینکه در تبارزایی شناسههای بیشتر با ارزشتر از تاکسونهای بیشترند. این عقیده منجر به مجادلهٔ شدیدی دربارهٔ نمونههای تاکسون شدهاست.
مطالعات تجربی، تئوری، و شبیهسازی منجر به اثباتهای متعددی از اهمیت نیاز به تعداد کافی نمونه تاکسون شدهاست. بیشتر اینها را میتوان به یک مشاهده ساده خلاصهسازی کرد: یک ماتریس داده فیلوژنتیک ابعادی به اندازهٔ کاراکترها در تاکسونها دارد. دو برابر کردن تعداد تاکسون منجر به دو برابر شدت اطلاعات میشود، دقیقاً همانند وقتی که تعداد شناسهها دو برابر شود. هر تاکسون نمایانگر یک نمونهٔ جدید برای هر کاراکتر است، اما بهطور مهمتر، تاکسون معمولاً نمایانگر یک ترکیب جدید از حالات کاراکترهاست. این حالات شناسهها نه تنها میتوانند مکان تاکسون روی درخت را مشخص کنند، بلکه میتوانند تمام اطلاعات کل تحلیل را بدهند.
اگرچه تا به حال مطالعات زیادی صورت گرفتهاست، هنوز کار زیادی روی استراتژیهای مربوط به نمونهگیری تاکسونها باید انجام شود. به دلیل پیشرفت در رایانهها و کاهش قیمت و افزایش خودکارسازی ترتیبدهی مولکولی (molecular sequencing)، اندازهٔ نمونهها بهطور کلی در حال افزایش اند و مطالعاتی که روابط بین صدها تاکسون را بررسی میکنند در حال رواج یافتن و عمومی شدن هستند. البته این بدین معنی نیست که اضافه کردن کاراکتر نمیتواند مفید باشد؛ تعداد کاراکترها نیز به همان شکل در حال افزایش است.
واکاوی
یک واکاوی (تحلیل) بیشینه صرفهجویی بسیار راحت و سرراست است. درختها بر اساس درجه و میزان بهینه بودن توزیع کاراکترها امتیاز دهی میشوند. بهینهترین درخت به عنوان درختی که طبق فرض روابط بین تاکسونها را بیان میکند انتخاب میشود.
درختها با استفاده از الگوریتم سادهای که، مشخص میکند چند گام برای توضیح دادن توزیع بین هر کاراکتر از دادهها لازم است ارزیابی میشوند. یک قدم لزوماً یک تغییر از یک وضعیت در یک کاراکتر به وضعیتی دیگر است، اگرچه با کاراکترهای مرتب بعضی از انتقالها به بیش از یک گام نیاز دارند. بر خلاف عقیدهٔ عموم الگوریتم بهطور صریح به گرهها وضعیت کاراکترها را نسبت نمیدهد: کمترین قدمها میتوانند شامل چندین مقداردهی و توزیع انتقال با هزینهٔ مساوی باشند و چیزی که بهینه میشود تعداد کل تغییرات است.
تعداد درختهای تبارزایشی ممکن برای هشت تاکسون یا بیشتر، بسیار بیشتر از این است که تماماً قابل جستجو باشند؛ بنابراین تعدادی از الگوریتمها برای جستجو بین درختهای ممکن به وجود آمدند. بسیاری از این روشها بر این اساس اند که ابتدا یک درخت اولیه میسازند و سپس این درخت را تغییر میدهند تا ببینند آیا درختی با امتیاز بیشتر بدست میآورند یا خیر.
درختهایی که از جستجوی پارسیمنی بدست میآیند بدون ریشهاند: آنها هرگونه ارتباط ممکن بین تاکسونها را نمایش میدهند اما فاقد هرگونه اطلاعات در مورد زمان نسبی انشعاب از یکدیگر هستند. یک شاخهٔ خاص توسط کاربر به عنوان ریشه انتخاب میشود. سپس این شاخه از بقیه شاخههای درخت به بیرون میآید تا در نهایت با یکدیگر یک گروه وابسته به یک ریشه تشکیل دهند. این نوعی از زمان نسبی را برای درخت بیان میکند. انتهاب نادرست ریشه میتواند منجر به روابط ناصحیح روی درخت شود، حتی اگر شکل بدون ریشهٔ درخت درست بوده باشد.
جک نایفینگ Jackknifing و بوت استرپینگ که از روشهای شناخته شدهٔ بازنمونهگیری هستند توسط تحلیل پارسیمنی به کار بسته شدهاند. جکنایف که شامل بازنمونهگیری بدون جایگذاری است میتواند روی تاکسونها یا کاراکترها به کار بسته شود. در حالت اول، یعنی بازنمونهگیری روی تاکسونها، تفسیرش ممکن است پیچیده شود؛ زیرا متغیر مورد نظر درخت است و مقایسه درختهایی با تاکسونهای مختلف کار سادهای نیست. بوت استرپ، که روش بازنمونهگیری با جایگذاری است، تنها روی کاراکترها استفاده میشود، زیرا اضافه کردن تاکسونهای دوگانه نتایج یک تحلیل پارسیمنی را تغییر نمیدهد. بوت استرپ بیشترین کاربردش در تبارزایش است. هر دوی روشها شامل تعدادی تکرار دلخواه ولی زیاد هستند؛ که هر تکرار شامل تغییر دادههای اصلی و سپس تحلیل آنهاست. درختهای با بیشترین صرفهجویی از هر تحلیل انتخاب میشوند و معمولاً نتایج روی یک درخت با قانون موافقت عمومی ۵۰ درصد از اکثریت همراه با شاخههایی که روی آنها درصد درختهای بیشینه صرفهجویی به دست آمده از بوت استرپ برچسبگذاری شدهاست به نمایش در میآید. این درصد بوت استرپ (که برخلاف بعضی از گفتهها یک p-value نیست) به عنوان معیاری برای پشتیبانی استفاده میشود. بهطور تکنیکی در واقع این معیاری برای قابلیت تکرارپذیری است، یا به عبارت دیگر احتمال اینکه اگر تاکسونها دوباره نمونهگیری شوند شاخهٔ مذکور مجدداً بازیابی شود. دادههای تجربی مربوط به انواع ویروسی پیشنهاد میدهند که درصد بوت استرپ تخمین خوبی برای قابلیت تکرارپذیری نیست، اما تخمین معقولی برای اندازهگیری دقت است. در حقیقت نشان داده شدهاست که درصد بوت استرپ به عنوان تخمین زنندهای از دقت، اریب است و این اریبی بهطور میانگین منجر به کم تخمین زدن اطمینان میشود (بطوریکه ۷۰ درصد پشتیبانی ممکن است در واقع ۹۵ درصد اطمینان را نشان دهد). اگرچه، جهت اریبی در موارد خاص نمیتواند تعیین شود، بنابراین فرض اینکه مقادیر بالای پشتیبانی بوت استرپ نشان دهندهٔ مقادیر بالاتری از اطمینان اند گارانتی نشدهاست.
مشکلات بیشینه صرفهجویی
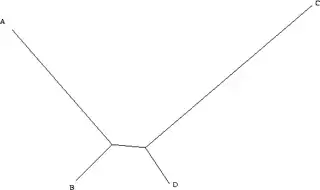
ماکزیمم پارسیمونی یک روش بسیار سادهاست وب همین دلیل مشهور است. اگرچه به صورت آماری سازگار (statistically consistent) نیست. بدین معنی که، با احتمال بالایی تضمین نمیکند که درختی که میدهد درخت بهینه باشد حتی اگر دادهها کافی باشند. همانطور که در سال ۱۹۸۷ توسط Joe Felsenstein[1] ثابت شد، ماکزیمم پارسیمنی تحت شرایط خاصی سازگار نیست. مواردی که در آنها این اتفاق میافتد long branch attraction نامیده میشوند و به عنوان مثال زمانی که طول شاخهها بری تو کاراکتر A,C بلند است اما برای دو شاخهٔ دیگر (B,D) کوتاه است اتفاق میافتد. A,B از یک پدر مشترک اند و همینطور C,D.
برای سادهسازی فرض کنید که ما یک کاراکتر دودویی تک را در نظر گرفتهایم (این کاراکتر میتواند + یا - باشد). به علت اینکه فاصلهٔ B تا D کم است، در بیشتر مواقع، B ,D مثل هم خواهند بود. در اینجا فرض میکنیم که هردو + باشند (+ و - به صورت دلخواه تعیین میشوند یا با یکدیگر جابهجا میشوند و این فقط به تعریف ربط دارد). اگر اینطور باشد، چهار حالت ممکن دیگر باقی میماند. A و C هر دو + باشند، که در این حالت تمام تاکسونها مثل هم اند و تمام درختها یک طول دارند. A میتواند + و C میتواند - باشد، که در این حالت فقط یک کاراکتر متفاوت است، و ما نمیتوانیم چیزی از آن یاد بگیریم، زیرا هر سه درخت در این حالت یک طول دارند. بهطور مشابه، A میتواند - و B میتواند + باشد. تنها حالت ممکنی که باقی میماند این است که A و C هر دو - باشند. در این حالت، A و C را در یک گروه با هم قرار میدهیم و B,D را هم با یکدیگر در گروهی دیگر قرار میدهیم. در نتیجه، وقتی درختی از این نوع داریم، هرچه بیشتر داده جمعآوری کنیم (مثلاً هرچه کاراکترهای بیشتری را مطالعه کنیم) گرایش و حرکت ما به سمت درخت اشتباه بیشتر خواهد بود.
انتقادات
گفته شدهاست که یک مشکل عمده، به ویژه در دیرینشناسی، این است که بیشینه صرفهجویی فرض میکند که تنها راهی که دو گونه میتوانند نوکلئوتیدها را در یک مکان به اشتراک بگذارند این است که بهطور ژنتیکی با هم در ارتباط باشند. این بدین معنی است که کاربردهای فیلوژنتیکی پارسیمنی فرض میکند که تمام شباهتها به خاطر هومولوگ بودن است؛ و بدون شک این درست نیست: مانند تمام روشهای دیگر که بر پایهٔ شناسهها هستند، پارسیمنی برای آزمایش طبیعت هومولوگی شباهتها است و این کار را با یافتن بهترین ساختاری که این شباهتها را توصیف کند انجام میدهد.
معمولاً بیان میشود که پارسیمنی ارتباطی با استنباط واقعی فیلوژنتیک ندارد. اما در بیشتر مواقع جایگزین صریحی برای آن پیشنهاد نمیشود؛ و وقتی که هیچ متد جایگزینی وجود نداشته باشد استفاده از هر متد آماری بهتر از استفاده نکردن از هیچ متد آماری است. آنالیز پارسیمنی از تعدادی تغییر در کاراکترها روی درخت استفاده میکند تا بهترین درخت را انتخاب کند، اما این به این معنی نیست که در واقع هم تمام این تغییرات اتفاق افتاده باشد. در عمل این تکنیک قدرتمند است، زیراماکزیمم پارسیمنی به دلیل انتخاب درخت با کمترین تغییرات کمترین اریبی را دارد.
بیشینه صرفهجویی همچنین گاهی اینگونه توجیه میشود که «سادهترین راه ممکن برای توجیه، بهترین راه است.»، یک تعمیم از اصل روکام. بیشینه صرفهجویی راهی را ترجیح میدهد که کمترین تعداد فرض بررسی نشده و نتایج غیرقابل پشتیبانی را داشته باشد. در واقع به دنبال راه حلی میگردد که فاصلهٔ تئوری تا دادهها را کم کند. این یک روش مشترک در علم است، مخصوصاً وقتی که مسئله به قدری پیچیدهاست که مدلهای ساده جوابگو نیستند. بیشینه صرفهجویی به هیچ وجه لزوماً یک فرض ساده را تولید نمیکند. در حقیقت، به عنوان یک قانون کلی، بیشتر کاراکترهای مجموعهٔ دادهها به قدری نویز دارند که حقیقتاً هیچ راه سادهای ممکن نیست.
جایگزینها
روشهای زیاد دیگری برای استنباط نژادها بر اساس دادههای کاراکتری وجود دارند؛ که هرکدام فواید و مضرات مربوط به خودشان را دارند. بیشتر این روشها طرفداران و مخالفان سرسختی دارند. بیشینه صرفهجویی بهطور ویژه به عنوان یک روشی که از نظر فلسفی قابل قبول است بیان میشود.
درستنمایی بیشینه
درستنمایی ماکزیمم یکی از معروفترین روشهای جایگزین است. درستنمایی ماکزیمم هم مانند پارسیمنی یک معیار سنجش بهینگی است. بهطور مکانیکی روش درستنمایی ماکزیمم همانند صرفهجویی درختها را بر اساس دادههای کاراکتری امتیازدهی میکند و درخت با بهترین امتیاز انتخاب میشود. این روش یک روش آماری پارامتری است. اینگونه متدها بالقوه قدرتمندتر از روشها غیر پارامتری مثل پارسیمنی هستند، اما تنها وقتی این مطلب درست است که مدلی که استفاده شدهاست تقریب خوبی از پروسهٔ به وجود آمدن دادهها باشد. میتوان گفت، درستنمایی ماکزیمم از نظر شهرت استفاده در دنباله-دادههای نوکلئوتیدی و استنباط تبارزایشی بیزی، از پارسیمنی پیشی گرفتهاست.
بهطور ساده، تخمین درستنمایی بیشینه مقادیری را برای پارامترهای مدل محاسبه میکند که در آن مقدار تابع درستنمایی بیشینه باشد. با استفاده از این روش، اگر توزیع دادهها معلوم باشد (مثلاً دادهها از توزیع نرمال پیروی کنند)، میتوان با در دست داشتن تنها چند نمونه از کل جامعهٔ هدف، تخمین خوبی از مقدار پارامترها در کل جامعهٔ هدف به دست آورد. مثلاً اگر توزیع قد زرافهها نرمال باشد، با استفاده از این روش میتوان تنها قد چند زرافه ماده را اندازه گرفت و به تخمین درستی از میانگین قد تمام زرافههای ماده رسید.
استنباط تبارزایشی بیزی
فیلوژنتیک بیزی از تابع دستنمایی استفاده میکند، و بهطور معمول از همان مدل ماکزیمم درستنمایی برای پیادهسازی اش استفاده میشود. در حالی که چه از نظر تئوری و چه در عمل کاملاً متفاوت است. فیلوژنتیک بیزی از قضیه بیز استفاده میکند، که احتمال پسین درخت را با درستنمایی دادهها مرتبط میسازد. اگرچه، برخلاف بیشینه صرفهجویی و روشهای درستنمایی، در این روش یک یا تعدای از درختهای بهطور مساوی بهینه تولید نمیشوند. تحلیل بیزی از درستنمایی درختها در شبیهسازی زنجیر مارکف مونت کارلو (Markov Chain Monte Carlo) برای نمونهگیری از درختها متناسب با میزان درستنمایی آنها بهره میبرد، بنابراین یک نمونه معتبر از درختها تولید میکند.
روشهای بر پایه ماتریس فاصلهها
روشهای غیر پارامتری بر مینای فاصله در ابتدا روی دادههای فنتیک(phenetic)با استفاده از فاصلههای دو به دو به کار برده شدند. این فاصلهها بعداً برای ساخت درخت (یک تبارنگار با شاخههای با طول دارای اطلاعات) مورد استفاده قرار گرفتند. ماتریس فاصلهها از منابع مختلفی میتواند به دست آید، شامل فاصلههای اندازهگیری شده (مثل فاصلههای به دست آمده در مطالعات ایمنیشناسی) یا تحلیلهای ریختسنجی، فرمولهای مختلف اندازهگیری فاصلهٔ بین دو جفت مثل فرمول اقلیدس هنگامی که برای کاراکترهای ریختشناسی گسسته مورد استفاده قرار میگیرد، یا فاصلههای ژنتیکی از دنبالهها. برای دادههای شناسهای تبارزایی، مقادیر فاصلههای خام میتوانند به سادگی با شمارش تعداد اختلافات وضعیت شناسهها در یک جفت محسابه کرد (فاصله منهتن) (Manhattan distance).
منابع
- Felsenstein, J. (1978). "Cases in which Parsimony or Compatibility Methods will be Positively Misleading". Systematic Biology. 27 (4): 401–410. doi:10.1093/sysbio/27.4.401. ISSN 1063-5157.
- مشارکتکنندگان ویکیپدیا. «Maximum Parsimony». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۷ می۲۰۱۱.