تابع مشخصه
فرض کنید X مجموعهای ناتهی و A زیرمجموعهای از X باشد. در این صورت تابع مشخصه A در X، یعنی (بخوانید خی A) را برای هر x∈X به صورت زیر تعریف میکنیم:
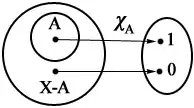
البته انتخاب مجموعه {۰٬۱} هر چند معمولتر است ولی الزامی نیست و میتوان هر مجموعه دو عضوی دیگر را نیز انتخاب کرد. این تابع به هر عضو مجموعه A، عدد یک و به هر عضو X-A یعنی عناصری که متعلق به X هستند ولی به A تعلق ندارند مقدار صفر را نسبت میدهد. وجه تسمیه این تابع این است که عناصری زیرمجموعه A از X را از سایر عناصری که در A قرار ندارند جدا میکند.
نمونهای از یک تابع مشخصه معروف تابع دیریکله است که همان تابع مشخصه Q(اعداد گویا) در R(اعداد حقیقی) است که آن را با D نشان میدهیم و به این صورت تعریف میکنیم:
به سادگی میتوان نشان داد این تابع در هیچیک از نقاط دامنه خود پیوسته نیست.
اگر بخواهیم به سادگی تابع بودن یک تابع را در نمودار پی ببریم کافی است که خط راستی موازی محورyها رسم کنیم اگر بیشتر ازیک نقطه محور را قطع کرد تابع نیست در غیراین صورت تابع بودن ان الزامی است