تابع هش
تابع هش (به انگلیسی: Hash function) یا تابع درهَمَکساز یا تابع چکیدهساز[1] به هر رویه خوش تعریف[2] یا تابع ریاضی میگویند که حجم زیادی از داده (احتمالاً حجم نامشخصی از داده) را به یک عدد طبیعی تبدیل کند. عدد طبیعی حاصل از تابع درهمسازی به عنوان اندیس یک آرایه مورد استفاده قرار می گیرد. مقادیر حاصل از این تابع را معمولاً مقدار هش یا فقط هش یا درهَمَک میخوانند. این توابع کاربردهای وسیعی در علوم کامپیوتر از جمله حفظ یکپارچگی داده ها دارند.
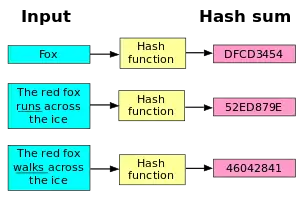
مقدمه
توابع درهمسازی بیشتر برای سرعت بخشیدن در جستجوی جدول های،فشردهسازی دادهها، درج یا حذف برای مجموعه پویایی که تعداد عناصر آن در طول زمان تغییر میکند، استفاده میشوند مانند جستجوی چیزی در یک پایگاه داده، تشخیص رکوردهای تکراری در حجم زیاد داده یا کشیدگیهای مشابه در دنباله دیانای (DNA) و بسیاری کاربردهای مشابه. در این مقاله دربارهٔ داده ساختاری به نام جدول درهمسازی و روش درهمسازی صحبت میکنیم که با طراحی درست همه این اعمال را در بدترین حالت و نیز در حالت میانگین با هزینهٔ انجام میدهد.
چیستی
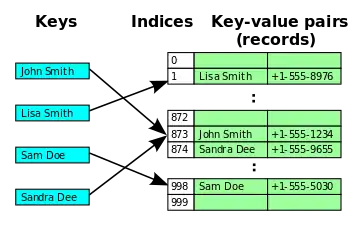
فرض کنید کلیدها اعداد صحیحی از یک تا ۱۰۰ باشند و حدود ۱۰۰ رکورد وجود دارد. یک روش کارآمد برای مرتبسازی رکوردها، ایجاد آرایه S با ۱۰۰ عنصر و نگهداری رکوردی با کلید i در [S[i است. بازیابی، بدون درنگ صورت میپذیرد و مقایسه کلیدها صورت نمیپذیرد. اگر حدود ۱۰۰ رکورد وجود داشته باشد و کلیدها، شمارههای شناسایی ۹ رقمی باشند، همین راهبرد را میتوان به کار برد ولی به لحاظ حافظه، کارایی بسیار کمی دارد زیرا آرایهای با یک میلیارد عنصر برای نگهداری تنها ۱۰۰ رکورد مورد نیاز است. به طریق دیگر، میتوانیم آرایهای با تنها ۱۰۰ عنصر که از ۰ تا ۹۹ اندیسگذاری میشود، ایجاد کنیم و هر کلید را به مقداری میان ۰ تا ۹۹ درهمسازی (به انگلیسی: Hash) کنیم. تابع درهمسازی تابعی است که هر کلید را به یک اندیس تبدیل میکند و استفاده از تابع درهمسازی در مورد یک کلید خاص را «کلید درهمسازی» (به انگلیسی: Hash key) میگویند. در مورد شمارههای شناسایی، یک تابع درهمسازی ممکن، عبارتاست از:
(٪ به معنای باقیمانده تقسیم کلید بر ۱۰۰ است) این تابع صرفاً دو رقم آخر کلید را بازمیگرداند. اگر یک کلید درهمسازی، به i درهمسازی شود، کلید و رکورد آن را در [S[i نگهداری میکنیم. این راهبرد کلیدها را به ترتیب نگهداری نمیکند، یعنی این تابع فقط در صورتی قابل استفادهاست که هرگز نیاز به بازیابی کارآمد دادهها به صورت ترتیبی نباشد. اگر نیاز به این کار باشد، یکی از روشهای بحث شده در قبل را باید به کار برد. اگر هیچ دو کلیدی به یک اندیس یکسان درهمسازی نشوند، این روش به خوبی عمل میکند. ولی هنگامی که تعداد قابل ملاحظهای کلید وجود داشته باشد، به ندرت چنین میشود. برای مثال، اگر ۱۰۰ کلید وجود داشته باشد تعداد حالاتی که هیچ دو کلیدی به یک اندیس یکسان درهمسازی نشوند نسبت به تعداد حالاتی که هر کلید به هر یک از ۱۰۰ اندیس درهمسازی شود، ، عبارت است از:
جدول آدرسدهی مستقیم
در آدرسدهی مستقیم فرض میکنیم که مجموعه جهانی U نسبتاً کوچک است و که m در آن خیلی بزرگ نیست، برای نمایش پویایی از این عناصر از آرایه به نام جدول آدرسدهی مستقیم استفاده میکنیم که در درایه iام تنها عنصری با کلید i میتواند قرار گیرد و درایههای دیگر خالی یا null هستند. اما هنوز این مشکل وجود دارد که این روش برای mهای بزرگ پاسخگو نیست و برای حل آن از جدول درهمسازی استفاده میشود.
نمایش اضافه شدن کلید جدید
تقریباً مطمئن هستیم که حداقل دو کلید به یک اندیس درهمسازی میشوند. چنین رویدادی را برخورد Collision یا تصادف میگویند. راههای گوناگونی برای برطرفکردن در برخوردها وجود دارد. یکی از بهترین راهها، استفاده از درهمسازی باز (یا آدرسدهی باز(به انگلیسی: Open Addressing)) است. برای درهمسازی باز، باکتی (سطل) برای هر مقدار درهمسازی ممکن ایجاد میکنیم و همه کلیدهایی را که به مقدار موجود در یک باکت درهمسازی میشوند، در باکت مربوط به آن قرار میدهیم. درهمسازی باز را معمولاً با لیستهای پیوندی پیادهسازی میکنند. برای مثال، اگر درهمسازی را به دو رقم آخر اعداد انجام دهیم، آرایهای از اشارهگرهای باکت را ایجاد میکنیم که از ۰ تا ۹۹ اندیسگذاری میشوند. همه آن کلیدهایی که به i درهمسازی میشوند در یک لیست پیوندی(به انگلیسی: Link List) که از [Bucket[i شروع میشود، قرار داده میشوند این نکته در شکل نشان داده شدهاست.
روش دیگری نیز برای برطرف کردن برخورد به نام روش زنجیرهای وجود دارد که در ادامه بیان خواهد شد.
نمایشی از درهمسازی باز و جدول درهمسازی
لازم نیست تعداد باکتها با تعداد کلیدها برابر باشد. برای مثال، اگر به دو رقم آخر درهمسازی کنیم، تعداد باکتها باید ۱۰۰ باشد؛ ولی، میتوانیم ۱۰۰۰، ۲۰۰، ۱۰۰ یا هر تعداد کلید را نگهداری کنیم. البته هر چه تعداد کلیدهایی که نگهداری کنیم بیشتر باشد، احتمال وجود برخورد بیشتر است. اگر تعداد کلیدها بزرگتر از تعداد باکتها باشد، حتماً برخورد داریم. چون باکت فقط یک اشارهگر را نگهداری میکند، فضای چندانی با اختصاص دادن به باکت اتلاف نمیشود؛ بنابراین، غالباً منطقی است که تعداد باکتها به اندازه تعداد کلیدها باشد. هنگام جستجو بهدنبال یک کلید، باید یک جستجوی ترتیبی در میان باکت (لیست پیوندی) حاوی کلید انجام دهیم. اگر همه کلیدها در یک باکت درهمسازی شوند، جستجو تا حد جستجوی ترتیبی تنزل مییابد. احتمال رخدادن آن چقدر است؟ اگر ۱۰۰ کلید و ۱۰۰ باکت داشته باشیم، احتمال آنکه کلیدها همگی به یک باکت ختم شوند، عبارت است از:
بنابراین، تقریباً برای همه کلیدها غیرممکن است که به یک باکت ختم شوند. دربارهٔ احتمال آن که ۷۰، ۸۰، ۹۰ یا هر تعداد دیگری از کلیدها به یک باکت ختم شوند، چه میتوان گفت؟ هدف اصلی ما این است که بدانیم احتمال آن که درهمسازی، در حالت میانگین به جستجویی بهتر از جستجوی دودویی بینجامد، چقدر است. نشان میدهیم که اگر به قدر کافی بزرگ باشد، این نیز تقریباً یک قطعیت به شمار میرود؛ ولی نخست نشان میدهیم که با درهمسازی، کارها چقدر بهتر میشود. بدیهی است بهترین حالتی که ممکناست رخ دهد این است که کلیدها به طور یکنواخت در باکتها توزیع شود. یعنی، اگر n کلید و m باکت وجود داشته باشد، هر باکت حاوی n/m کلید میشود. در واقع هر باکت دقیقاً هنگامی حاوی n/m کلید میشود که n مضرب m باشد. اگر چنین نباشد، یک توزیع نسبتاً یکنواخت خواهیم داشت. قضیههای زیر نشان میدهد که وقتی کلیدها به طور یکنواخت توزیع شده باشند، جه اتفاقی میافتد. برای سادگی، آنهارا برای توزیعی دقیقاً یکنواخت بیان میکنیم (یعنی برای موردی که n مضربی از m باشد).
روش زنجیرهای برای حل برخورد
در روش زنجیرهای عناصری را که به وسیله تابع درهمسازی به یک درایه از جدول درهمسازی- مثلاً iS- نگاشته میشوند به صورت یک لیست خطی یکسویه درمیآوریم و آدرس شروع آن را در همان درایه، یعنی قرار میدهیم. در حالت کلی عناصر با کلیدهای مختلف k که مقدار آنها برابر است در لیست پیوندی قرار میگیرند و درایههای خالی جدول هم لیستهای تهی هستند، به چنین جدولی، جدول درهمسازی با روش زنجیرهای میگوییم. در این روش اعمال درج در زمان انجام میشود، اما عمل جستجو و حذف با یک عمل جستجوی عنصر همراه است که در بدترین حالت هزینهای متناسب با طول لیست دارد.
توابع درهمسازی
یک تابع درهمسازی خوب تابعی است که ساده و یکنوا باشد، در ادامه یکی روشهای سادهٔ مختلف را برای طراحی تابع درهمسازی را بیان میکنیم.
روش ضرب
در این روش ابتدا کلید k را در یک عدد ثابت A که است ضرب کنیم و قسمت اعشاری آن را بدست آوریم. یعنی:
فرض کنید که کلمهٔ کامپیوتر w بیتی است و k در یک کلمه جای میگیرد. A را طوری انتخاب میکنیم که برابر باشد، که در آن s یک عدد صحیح در محدودهٔ باشد. ابتدا k را در عدد صحیح w بیتی ضرب میکنیم و حاصل ضرب یک عدد 2w بیتی به صورت است که کلمهٔ پر ارزش و کلمهٔ کمارزش حاصل ضرب است. عدد p بیتی تابع درهمسازی مورد نظر، p بیت پرارزش است.
درهمسازی دوگانه
اگر دو رکورد در توابع درهم سازی به یک مکان در فایل انتقال یابند به آن برخورد میگویند. روش ایدئال برای مقابله با برخوردها این است که بتوان الگوریتم تبدیلی پیدا کرد که به طور کلی از وقوع برخوردها جلوگیری کند.
یکی از راههای جلوگیری از برخورد استفاده از روش وارسی خطی است.
روش وارسی خطی با داشتن یک تابع در هم ساز کمکی به نام از تابع زیر برای درهم سازی استفاده میکند:
به ازای i = ۰ , ۱ , … m-1 به ازای یک کلید k، ابتدا را وارسی میکنیم سپس به و بعد به میرویم و این کار را به صورت حلقوی ادامه میدهیم تا به برسیم. در این حالت فقط m دنبالهٔ وارسی مجزا تولید میشود. درهم سازی دوگانه یک روش وارسی است که در آن توابع در هم سازی به صورت زیر است:
که در آن توابع h و g تابههای درهم ساز کمکی هستند. اولین وارسی در انجام میشود و وارسیهای بعدی به درایهای با فاصله میرود. مثالی از این درج در شکل زیر آمدهاست، در این مثال، m=۱۳ و و است.
چون h(14) = ۱ و g(14) = ۴ است بنابراین کلید ۱۴، پس از آنکه درایههای ۱ و ۵ وارسی شده و پر بودند در درایهٔ خالی ۹ درج میشود.
در طراحی این درهم سازی باید مقدار نسبت به m اول باشد تا اینکه کلیهٔ درایههای جدول وارسی شوند. یک روش مناسب انتخاب m به صورت توان ۲ و طراحی g به طوری است که همیشه یک عدد فرد تولید کند. یک روش دیگر آن است که m عدد اول باشد و g همیشه یک عدد صحیح و مثبت کوچکتر از m را تولید کند.
درهم سازی دوگانه نسبت به وارسی خطی و وارسی درجهٔ ۲ بهتر عمل میکند، زیرا به تعداد در مقایسه با دنبالهٔ وارسی تولید میکند؛ بنابراین به نظر میرسد کارایی این درهم سازی به کارایی درهم سازی یکنوا نزدیکتر باشد.
درهمسازی سراسری
در هنگام استفاده از توابع درهم سازی اگر تابعی که مورد استفادهٔ ماست توسط کاربر فهمیده شود، کاربر میتواند دادههایش را طوری وارد کند که تعداد برخوردها زیاد باشند. برای جلوگیری از این اتفاق، از درهم سازی سراسری استفاده میکنیم.
یک خانواده از توابع درهم ساز به اسم H را فرض کنید.
میگوییم H یک خانواده از توابع درهم ساز سراسری است اگر: در ازای هر دو کلید k1 و k2 که عضو مجموعهٔ کلیدهای مورد نظر ما هستند، تعداد توابع درهم ساز مانند h که عضو H هستند به طوری که حداکثر برابر باشد.
هنگامی که کاربر مجموعهای از دادهها را وارد میکند به صورت تصادفی یکی از توابع درهم سازی را انتخاب میکنیم و ورودیها را با استفاده از آن تابع در حافظه ذخیره میکنیم. در این صورت دیگر کاربر نمیتواند حدس بزند که چه تابعی انتخاب شده و در نتیجه نمیتواند مقادیر ورودی را طوری تعیین نماید که تعداد برخوردها زیاد باشد.
درهمسازی کامل
گاهی ما در درهمسازی با کلیدهای ایستا- که از قبل معلوم هستند- سروکار داریم، در این حالت یک روش درهمسازی را کامل مینامیم اگر در بدترین حالت تعداد دسترسیها به حافظه برای یک عمل جستجو باشد. ایدهٔ اصلی این نوع درهمسازی استفاده از دو سطح درهمسازی و یک تابع درهمسازی سراسری برای هر سطح است.
درهمسازی پویا
در روشهایی که تا کنون برای درهمسازی بحث کردهایم فرض بر میشود که تعداد عناصر حداکثر برابر اندازهٔ جدول- روش باز- یا تقریباً برابر آن- روش زنجیرهای- است در حالی که در بسیاری از مواقع تعداد عناصر از پیش مشخص نیست و نمیتوان کران بالای خوبی برای اندازهٔ جدول درهمسازی پیشبینی کرد که باعث اتلاف حافظه نشود.
برای حل این مشکل از روش درهمسازی پویا استفاده میشود که در آن اندازه جدول متناسب با نیاز متغیر است؛ که برای تغییر اندازه جدول نیز باید هزینه کنیم اما نشان داده شده است که حتی با هزینه لازم برای تغییر اندازه جداول همچنان کل هزینه برابر
میماند.
جستارهای وابسته
پانوشتها
- «تابع چکیدهساز» [رمزشناسی] همارزِ «cryptographic hash function, hashing algorithm, hash function»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر نهم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۱۸-۴ (ذیل سرواژهٔ تابع چکیدهساز)
- الگوریتم
منابع
- جعفرنژاد قمی، عینالله. طراحی الگوریتمها. چاپ ششم، انتشارات علوم رایانه، ۱۳۸۳.
- مترجمین: گروه مهندسی-پژوهشی خوارزمی.مقدمهای بر الگوریتمها. انتشارات دقت، ۱۳۸۷.
- مشارکتکنندگان ویکیپدیا. «Hash function». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۵ نوامبر ۲۰۰۸.
- مشارکتکنندگان ویکیپدیا. «Hash». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳ می ۲۰۱۱.
- مشارکتکنندگان ویکیپدیا. «Hash key». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳ می ۲۰۱۱.
- مشارکتکنندگان ویکیپدیا. «Hash table». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳ می ۲۰۱۱.
- مشارکتکنندگان ویکیپدیا. «Link exchange». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳ می ۲۰۱۱.
- قدسی، محمد، داده ساختارها و مبانی الگوریتمها، چاپ دوم، انتشارات فاطمی، ۱۳۸۹.