تحلیل سرشکنی

تحلیل سرشکنی[1]

در علوم کامپیوتر به خصوص در تحلیل الگوریتم‌ها، تحلیل سرشکنی زمان اجرای میانگین برای هر دستور را در بدترین حالت بدست می‌آورد. تحلیل سرشکنی با متوسط زمان اجرا تفاوت دارد چرا که زمان اجرای هر دستور در بدترین حالت را بیان می‌کند.

گاهی به دنبال روشی برای پیدا کردن زمان اجرای یک رویه هستیم. برای این کار، گاهی پیشنهاد می‌شود که به‌طور مستقیم بدترین زمان اجرا را بدست آوریم. این عمل باعث می‌شود که همیشه یک زمان اجرای خیلی زیاد بدست آید. اما تحلیل سرشکنی این امکان را به ما می‌دهد تا زمان اجرایی بسیار نزدیک به زمان اجرای واقعی بدست آوریم.

• 
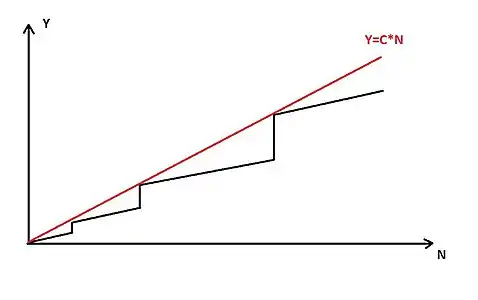  تحلیل زمانی آرایه پویا

شبه کد تحلیل سرشکنی

اینجا هدف این است که هزینه‌ی یک عمل را بدون توجه به ورودی به دست بیاوریم. مثلاً اگر یک شمارنده بیتی داشته باشیم، هزینه‌ی هر بار زیاد کردن آن برابر است با هزینه‌ی شمردن تا عددی که الان در شمارنده وجود دارد:

ولی اگر بخواهیم مستقل از مقدار فعلی شمارنده به دست بیاوریم، زمانش (O(1 می‌شود.

این روش (تحلیل سرشکنی) در واقع:

• میانگین اجرای هر عمل در بدترین حالت را بدست می‌ آورد.
• مربوط به اجرای کل برنامه‌ است نه دستورهای خاصی از برنامه.
• این تحلیل این‌گونه تفسیر می‌شود که بعضی از دستورهای پر هزینه در آینده برای دستورهایی که هزینه‌ی کمتری دارند خرج شود.

در این تحلیل از ۳ روش زیر استفاده می‌شود:

I. روش انبوهه[2]

II. روش حسابداری[3]

III. روش تابع پتانسیل[4]

هر ۳ روش ذکر شده جواب درستی به ما می دهند و انتخاب استفاده از این ۳ روش بستگی به این دارد که کدام یک برای یک موقعیت خاص مناسب تر باشد.

تاریخچه

تحلیل سرشکن شده در ابتدا از روشی به نام تحلیل متراکم پدید آمده که امروزه شامل تحلیل سر شکن است. این تکنیک بار اول توسط رابرت تارجان در مقاله پیچیدگی محاسباتی وقف شده‌اش در سال ۱۹۸۵ معرفی شد. که نیاز به یک شکل مفیدتر از تحلیل روشهای احتمالی متداول مورد استفاده را برطرف می کند. سرشکنی در ابتدا برای انواع خاصی از الگوریتم‌ها مورد استفاده قرار می گرفت، به ویژه آنهایی که مربوط به درختان باینری[5] و عملیات یونیون [6]هستند. با این حال، امروزه هم از این تحلیل کاربرد های زیادی دارد و هنگام تحلیل بسیاری از الگوریتم های دیگر نیز مورد استفاده قرار می گیرد.

روش انبوهه

در روش انبوه[2] ابتدا باید هزینه‌ی پی در پی اجرای n عملیات را محاسبه کنیم که در کل هزینه‌ی آن دنباله‌ای از n عملیات است و زمان اجرای آن ${\displaystyle T(n)}$ است و سپس آن را بر تعداد (n) تقسیم کرده و در نتیجه هزینهٔ میانگین یا سرشکن شده که برابر T(n) / n است برای هر عمل بدست می‌آید. برای استفاده از این روش باید هر عمل و هزینهٔ اجرای آن را شناسایی کرد.

برای تحلیل شمارنده با این روش این‌گونه در نظر گرفته می‌شود که اگر تغییر بیت‌های در هر مرحله را در نظر بگیریم در مجموع برابر با ۲n و در نتیجه زمان اجرای آن ${\displaystyle o(n)}$ می‌شود.

روش حسابداری

روش حسابداری[3] نوعی از تحلیل انبوه است که به هر عمل یک هزینه‌ی سرشکن شده اختصاص میابد که ممکن است با هزینه‌ی واقعی متفاوت باشد.

در این روش در ابتدا یک سری عملیات ابتدایی که در الگوریتم مورد استفاده قرار می‌گیرند را انتخاب می‌کنیم و به صورت دلخواه هزینه‌ی آن‌ها را ۱ در نظر می‌گیریم.

به هر مجموعه عملیات یک هزینه نسبت داده می‌شود و عملیاتی که هزینه‌ی کمتری دارند پولشان برای هزینه‌های بعدی ذخیره می‌شود.

میزان پول پرداختی برای هر عمل با هزینه‌ی سرشکنی آن متناسب است.

برای این داده ساختار به ازای هر عمل ۲ریال هزینه می‌کنیم که این ۲ریال صرف تغییر ۰ به ۱ و بالعکس می‌شود.

به صورت کلی هنگامی که هزینه سرشکن شده یک عمل از هزینه واقعی آن تجاوز کند، اختلاف این هزینه به عنوان موجودی به اشیایی مشخص در ساختمان داده اختصاص می‌یابد. موجودی بعداً می‌تواند در جهت کمک به پرداخت برای اعمالی که هزینه سرشکن شده آنها کمتر از هزینه واقعی شان است مورد استفاده قرار گیرد. بنابراین می‌توان هزینه سرشکن شده یک عمل را مشاهده کرد که بین هزینه واقعی آن و موجودی که پرداخت شده یا استفاده می‌شود، تقسیم شده‌است. این روش با تحلیل جمعی که در آن تمام اعمال هزینه‌های سرشکن شده یکسانی دارند، بسیار متفاوت است. هزینه‌های سرشکن شده اعمال باید به دقت انتخاب شوند. اگر بخواهیم تحلیل را با هزینه‌های سرشکن شده انجام دهیم تا نشان دهیم که در بدترین حالت هزینه میانگین هر عمل کم است، کل هزینه سرشکن شده یک توالی از اعمال باید یک حد بالا برای هزینه کل واقعی توالی باشد. علاوه بر این همانند تحلیل جمعی، این رابطه باید برای تمام توالی‌های اعمال برقرار باشد. اگر هزینه واقعی ${\displaystyle i}$ امین عمل را با  ${\displaystyle c_{i}}$ و هزینه سرشکن شده ${\displaystyle i}$ امین عمل را با  ${\displaystyle {\widehat {c}}_{i}}$ نشان دهیم، برای تمام توالی‌هایی از عمل ${\displaystyle n}$ داریم:

${\displaystyle \sum _{i=1}^{N}{\widehat {c}}_{i}\geqq \sum _{i=1}^{N}{c}_{i}}$

بنا به نامساوی بالا کل موجودی مربوط به ساختمان داده باید در همه زمان‌ها نامنفی باشد. اگر کل موجودی می‌توانست منفی باشد(در نتیجه پرداخت ارزش کم به عمل‌های قبلی، با این تعهد که دوباره پس از آن پرداخت صورت گیرد) آنگاه کل هزینه‌های سرشکن شده ایجاد شده در آن هنگام کمتر از کل هزینه‌های واقعی ایجاد شده می‌بود؛ برای توالی عمل‌ها تا آن زمان کل هزینه سرشکن شده یک حد بالا برای کل هزینه واقعی نمی‌بود. بنابراین باید مراقب باشیم تا موجودی کل در ساختمان داده هرگز منفی نشود.

روش شارژ کردن

تعدادی از هزینه را روی اعمال قبلی شارژ می‌کنیم.

هزینه‌ی سرشکن:

هزینه‌ای که در آینده، بقیه عمل ها روی این عمل شارژ می‌شوند + هزینه‌ای که روی بقیه شارژ می‌کنیم - هزینه‌ی واقعی

روش تابع پتانسیل

روش تابع پتانسیل[4] نوعی از روش حسابداری است که در آن اعتبار ذخیره شده به عنوان تابعی از وضعیت داده ساختار محاسبه می‌شود. هزینه سرشکنی هزینه بدیهی به علاوه تغییر پتانسیل است.

راه دیگر پیدا کردن هزینهٔ سرشکنی استفاده از تابع پتانسیل است. در این روش به داده ساختار داده شده یک تابع پتانسیل نسبت می‌دهیم و با یک ساختمان داده اولیه ${\displaystyle D_{0}}$ را شروع می‌کنیم که روی آن ${\displaystyle n}$ عمل انجام می‌شود. برای هر ${\displaystyle i=1,2,\cdots ,n}$، ${\displaystyle c_{i}}$ را هزینه واقعی ${\displaystyle i}$ امین عمل قرار می‌دهیم و ${\displaystyle D_{i}}$ را ساختمان داده‌ای که پس از به کارگیری ${\displaystyle i}$ امین عمل روی ساختمان داده ${\displaystyle D_{i-1}}$ حاصل می‌شود، قرار می‌دهیم. تابع پتانسیل[7] هر ساختمان داده ${\displaystyle D_{i}}$ را به یک عدد حقیقی ${\displaystyle \phi (D_{i})}$ نگاشت می‌کند. این عدد، پتانسیل مربوط به ساختمان دادهٔ ${\displaystyle D_{i}}$ است. هزینه سر شکن شده ${\displaystyle {\hat {c}}_{i}}$ مربوط به ${\displaystyle i}$ امین عمل با توجه به تابع پتانسیل ${\displaystyle \phi }$ به صورت زیر تعریف می‌شود:

${\displaystyle {\hat {c}}_{i}=c_{i}+\phi (D_{i})-\phi (D_{i}-1)}$

براین هزینه سرشکن شده هرعمل برابرهزینه واقعی آن به علاوه افزایش پتانسیل حاصل از عمل می‌باشد. بنا به معادله بالا، هزینه سرشکن شده کل ${\displaystyle n}$ عمل برابر است با:

${\displaystyle \sum _{i=1}^{n}{\hat {c}}_{i}=\sum _{i=1}^{n}\left(c_{i}+\phi (D_{i})-\phi (D_{i-1})\right)=\sum _{i=1}^{n}c_{i}+\phi (D_{n})-\phi (D_{0})}$

اگر بتوانیم یک تابع پتانسیل ${\displaystyle \phi }$ تعریف کنیم بطوریکه ${\displaystyle \phi (D_{n})>=\phi (D_{0})}$، آنگاه هزینه سرشکن شده کل ${\displaystyle \sum _{i=1}^{n}{\hat {c}}_{i}}$، یک حد بالا برای هزینه واقعی کل ${\displaystyle \sum _{i=1}^{n}c_{i}}$ می‌باشد. در عمل همواره نمی‌دانیم چه تعداد عمل ممکن است انجام شود. بنابراین اگر برای تمام ${\displaystyle i}$ها تأکید کنیم که${\displaystyle \phi (D_{n})>=\phi (D_{0})}$، آنگاه همانند روش حسابداری تضمین می‌کنیم که از پیش هزینه را پرداخت کرده‌ایم. اغلب مناسب است که ${\displaystyle \phi (D_{0})}$ را 0 تعریف کنیم و آنگاه نشان دهیم که برای تمام ${\displaystyle i}$ها، ${\displaystyle \phi (D_{i})>=0}$. به‌طور شهودی اگر اختلاف پتانسیل ${\displaystyle \phi (D_{i})-\phi (D_{i-1})}$ از ${\displaystyle i}$ امین عمل مثبت باشد آنگاه هزینه سرشکن شده ${\displaystyle {\hat {c}}_{i}}$ یک پرداخت اضافه به ${\displaystyle i}$ امین عمل را نشان می‌دهد، و پتانسیل ساختمان داده افزایش می‌یابد. اگر اختلاف پتانسیل منفی باشد، آنگاه هزینه سرشکن شده، یک پرداخت کم به ${\displaystyle i}$ امین عمل را نشان می‌دهد و هزینه واقعی عمل با کاهش پتانسیل پرداخت می‌شود. هزینه‌های سر شکن شده تعریف شده به وسیله دو معادلهٔ بالا به انتخاب تابع پتانسیل ${\displaystyle \phi }$ بستگی دارد. توابع پتانسیل متفاوت ممکن است به هزینه‌های سرشکن شده متفاوت که همچنان حدود بالا برای هزینه‌های واقعی اند منجر گردند. اغلب در انتخاب یک تابع پتانسیل مبادلاتی می‌توانند انجام گیرند؛ بهترین تابع پتانسیل جهت استفاده بستگی به حدود زمانی مطلوب دارد.

بهتر است که تابع پتانسیل:

1. منفی نباشد.
2. ساده باشد.
3. بازتاب دقیقی از هزینه‌های موجود در داده ساختار (مثلاً خالی کردن آن) باشد.

تابع پتانسیلی که در این روش در نظر گرفته می‌شود معادل با تفاوت تعداد ۰ و ۱ ها در هر مرحله می‌باشد. (${\displaystyle t_{i}}$ معادل با تعداد بیت‌های تغییر یافته از ۰ به ۱ و بالعکس می‌باشد)

${\displaystyle {\hat {c}}_{i}=c_{i}+\phi (D_{i})-\phi (D_{i}-1)}$

${\displaystyle \phi (D_{i})-\phi (D_{i}-1)<=-(t_{i})+1}$

${\displaystyle c_{i}<=t_{i}+1}$

در نتیجه

${\displaystyle c_{i}<=2}$

مثال ها

آرایه پویا

تحلیل سرشکن شده از عملیات اضافه کردن برای یک آرایه پویا

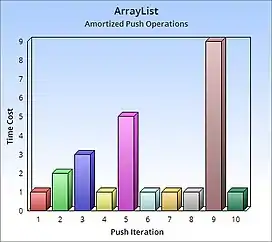
یک آرایه پویا را در نظر بگیرید که با افزودن عناصر بیشتر به آن ، اندازه‌ی این آرایه بیشتر میشود، مثل ArrayList در جاوا و std::vector در ++C. به طور مثال اگر از آرایه‌ای به اندازه‌ی ۴ شروع کنیم، می‌توانیم این ۴ عنصر را به آن اضافه کنیم و هرکدام از این عملیات یک زمان ثابت دارد. با این حال اضافه کردن عنصر پنجم به این آرایه زمان بیشتری می‌برد به دلیل آنکه باید یک آرایه‌ی جدید که اندازه‌ی آن ۲ برابر آرایه‌ی فعلی (۸) است بسازد، حال عناصر قدیمی را در یک آرایه‌ی جدید کپی کنید و سپس عنصر جدید را اضافه کنید. سه عملیات بعدی اضافه کردن نیز به طور مشابه زمان ثابت می‌برد. سپس افزودن مقدار بعدی نیازمند دو برابر شدن آرایه است که سرعت این عمل بسیار کند است. اگر به طور کلی در یک آرایه‌ی به اندازه‌ی n تعداد دلخواه اضافه کردن ها را n + 1 نظر بگیریم، ما متوجه می‌شویم که اضافه کردن این عملیات در یک زمان ثابت انجام می‌شود به جز آخری که ${\displaystyle \Theta (n)}$ طول می‌کشد. از آنجا که در کل n + 1 عملیات وجود دارد می‌توانیم از میانگین آن استفاده کنیم و در یابیم که اضافه کردن عناصر بر روی یک آرایه پویا ${\displaystyle {\tfrac {n\Theta (1)+\Theta (n)}{n+1}}=\Theta (1)}$ طول می‌کشد، در زمان ثابت.

تحلیل شمارندهٔ دودویی

ادعا: به صورت سرشکن در هر مرحله (O(1 رقم تغییر می‌کند.

حداکثر تلاش اول برای تعداد ۱ های سمت راست = k +1 - Δ(ϕ)

طبق فرمول تابع پتانسیل

Q۳	Q۲	Q۱	Q۰
۰	۰	۰	۰
۰	۰	۰	۱
۰	۰	۱	۰
۰	۱	۱	۱
۱	۰	۰	۰

تحلیل سرشکن شده در درج درخت قرمز سیاه

بگذارید با استفاده از روش تابع پتانسیل در مورد سرشکنی درج درخت قرمز سیاه بحث کنیم:

ابتدا ما یک تابع ${\displaystyle \phi }$ تعریف می‌کنیم که مقدار واقعی غیرمنفی یک داده ساختار را به ما می‌دهد که نتیجه‌ی این عملیات می‌تواند باعث تغییر مقدار این تابع پتانسیل شود.

در عکس زیر مقدار تابع پتانسیل ${\displaystyle \phi }$ را تعریف می‌کنیم:

در تصویر بالا n تعداد رئوس درخت قرمز-سیاه می‌باشد.

تابع پتانسیل کل رئوس این درخت قرمز-سیاه ${\displaystyle \phi =\sum g(n)}$ است.

و همچنین :

هزینه‌ی سرشکنی = c+Δϕ(h)

که طبق تابع پتانسیل (Δϕ(h برابر است با (h’) –  ${\displaystyle \phi }$(h)${\displaystyle \phi }$ و c نیز هزینه‌ی سرشکن ما می‌باشد.

تغییر تابع پتانسیل باید به گونه‌ای باشد که برای عملیات کم هزینه مثبت و برای عملیات پر هزینه منفی باشد.

رأس جدیدی که در یکی از عضو های درخت قرمز-سیاه درج می‌شود یکی از انواع زیر را دارد:

درج و تحلیل سرشکنی در شکل زیر نشان داده شده‌است:

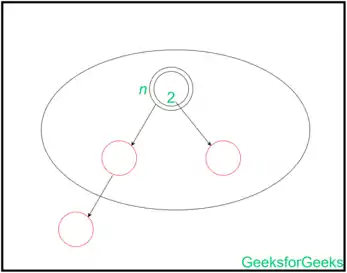
این درج ابتدا از تغییر رنگ والدین (قرمز) شروع می‌کند و بچه ها را هم قرمز می‌کند و سپس به سراغ پدربزرگ و عموی همان عضو را رنگ می‌کند که دو حالت پیش می‌آید:

۱- جد آن برگ قرمز است.

۲- عمو و جد یک عضو هر دو سیاه باشند.( که ممکن است عموی آن عضو قرمز و جدش سیاه است و یا بالعکس)

این موضوع در شکل زیر نیز مشخص است:

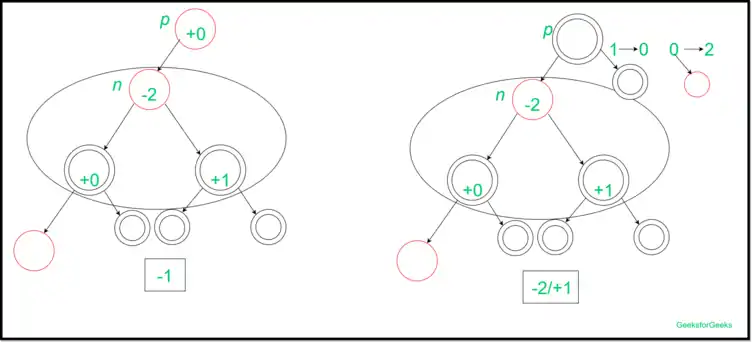
در این درج، رأس بدون هیچگونه تغییری درج می‌شود زیرا عمق درخت یکسان است این در شرایطی است که عضو ما ممکن است خواهر و برادر سیاه داشته باشد و یا اصلا خواهر و برادری نداشته باشد.

در نتیجه هزینه‌ی سرشکن شده در این درج 0 می‌باشد.

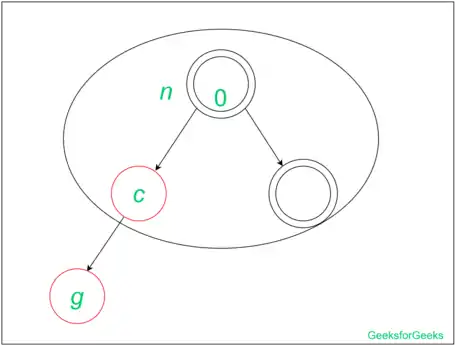
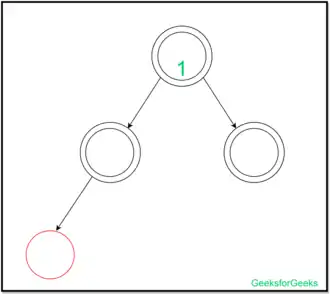
در این درج ما نمی‌توانیم عضو رأسی را تغییر رنگ دهیم زیرا اگر والد و خواهر و برادرش سیاه باشند، سیاه می‌مانند در نتیجه ما باید درخت را به چپ چرخش دهیم.

بعد از چرخش همانند شکل زیر برای پر رأسی همانند رأس g اتفاقی نیافتاده و این رأس که سیاه بوده، سیاه باقی مانده و برای جد رأس g نیز که قرمز است باز تغییری صورت نگرفته و این رأس قرمز باقی می‌ماند.

در نتیجه هزینه‌ی سرشکن شده‌ی آن طبق شکل زیر ۲+ می‌باشد.

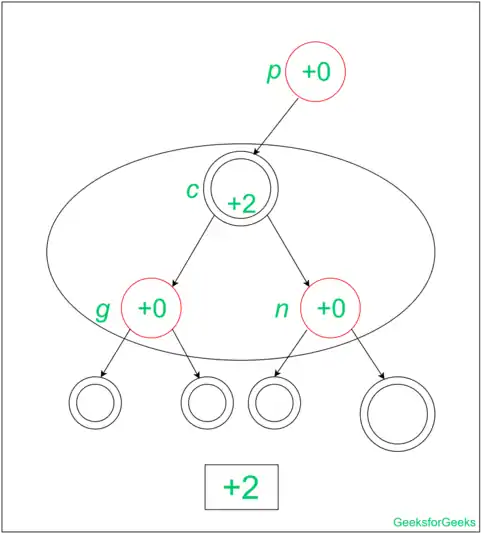
بعد از محاسبه کردن این موارد خاص برای محاسبه کردن هزینه‌ی تحلیل سرشکنی حال می‌توانیم درباره‌ی هزینه‌ی سرشکنی آن در حالت کلی بحث کنیم.

در صورتی که بدانیم n تعداد کل رئوس ماست داریم: ${\displaystyle \Delta \phi (h)\leqq n}$

در نتیجه هزینه کل سرشکن شده در درخت قرمز-سیاه برابر (O(n می‌باشد.

منابع

کتاب CLRS

https://en.wikipedia.org/wiki/Amortized_analysis#cite_note-fiebrink-2

https://en.wikipedia.org/wiki/Data_structure

http://en.wikipedia.org/wiki/Accounting_method

http://en.wikipedia.org/wiki/Amortized_analysis

http://www.cs.cmu.edu/afs/cs.cmu.edu/academic/class/15750-s03/www/amortized-analysis.txt

https://web.archive.org/web/20081220170554/http://www.academic.marist.edu/~jzbv/ads/AmortizedAnalysis.htm

Berkeley Lecture 35: Amortized Analysis

MIT Lecture 13: Amortized Algorithms, Table Doubling, Potential Method

http://www.cs.cornell.edu/courses/cs3110/2011sp/lectures/lec20-amortized/amortized.htm

پانویس

1. "Amortized analysis". Wikipedia. 2020-05-11.
2. aggregate method
3. accounting method
4. potential function method
5. "Binary tree". Wikipedia. 2020-05-12.
6. "Union type". Wikipedia. 2020-05-11.
7. potential function