میانگین

چندین گونه برای میانگین[1] (به انگلیسی: Mean) در ریاضیات و به‌ویژه در آمار وجود دارد. در مطالعه توزیع یک جامعه آماری مقدار نماینده که اندازه‌ها در اطراف آن توزیع شده‌اند را مقدار مرکزی می‌نامند و هر معیار عددی را که معرف مرکز مجموعه داده‌ها باشد، معیار گرایش به مرکز می‌نامند. میانگین و میانه از متداول‌ترین معیارهای گرایش به مرکز هستند.[2]

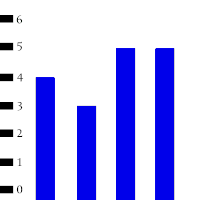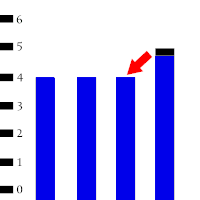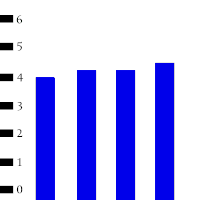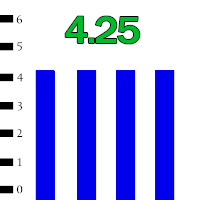
میانگین به روش تصویری

انواع

میانگین در ریاضیات و آمار کاربرد متفاوت دارد، که شامل

• میانگین حسابی، میانگین حسابی ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ به این شکل تعریف می‌شود:
  • ${\displaystyle {\bar {x}}={\frac {1}{n}}\left(\sum _{i=1}^{n}{x_{i}}\right)={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}}$
  • مثال: میانگین حسابی ${\displaystyle 4,36,45,50,75}$ برابر است با ${\displaystyle {\frac {4+36+45+50+75}{5}}={\frac {210}{5}}=42}$
• میانگین هندسی، میانگین هندسی ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ به این شکل تعریف می‌شود:
  • ${\displaystyle {\bar {x}}=\left(\prod _{i=1}^{n}{x_{i}}\right)^{\frac {1}{n}}=\left(x_{1}x_{2}\cdots x_{n}\right)^{\frac {1}{n}}}$
  • مثال: میانگین هندسی ${\displaystyle 4,36,45,50,75}$ برابر است با ${\displaystyle (4\times 36\times 45\times 50\times 75)^{\frac {1}{5}}={\sqrt[{5}]{24\;300\;000}}=30}$
• میانگین هارمونیک، میانگین هارمونیک ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ به این شکل تعریف می‌شود:
  • ${\displaystyle {\bar {x}}=n\left(\sum _{i=1}^{n}{\frac {1}{x_{i}}}\right)^{-1}}$
  • مثال میانگین هارمونیک ${\displaystyle 4,36,45,50,75}$ برابر است با ${\displaystyle {\frac {5}{{\tfrac {1}{4}}+{\tfrac {1}{36}}+{\tfrac {1}{45}}+{\tfrac {1}{50}}+{\tfrac {1}{75}}}}={\frac {5}{\;{\tfrac {1}{3}}\;}}=15}$
• و در آمار به امید ریاضی که یک متغیر تصادفی است و همچنین میانگین جامعه آماری نامیده می‌شود.

میانگین‌های دیگری نیز در دانش‌های گوناگون کاربرد دارند که از میان شناخته‌شده‌ترین آن‌ها می‌توان میانگین وزنی را نام برد.

مقایسه میانگین، میانه و مد

مقایسه مشترک متوسط ریاضی در مجموعه { ۱, ۲, ۲, ۳, ۴, ۷, ۹ }

نوع	توضیح	مثال	نتیجه
میانگین حسابی	جمع ارزش یک مجموعه داده تقسیم بر تعداد ارزش‌ها: ${\displaystyle \scriptstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$	۷ / (۱+۲+۲+۳+۴+۷+۹)	۴
میانه (آمار)	ارزش عددی واقع شده در وسط یک مجموعه داده پس از حذف بزرگترین و کوچکترین داده از مجموعه	۱, ۲, ۲, ۳, ۴, ۷, ۹	۳
مد	پر تکرارترین ارزش در یک مجموعه داده	۱, ۲, ۲, ۳, ۴, ۷, ۹	۲

جستارهای وابسته

• نمونه (آمار)
• میانه (آمار)

منابع

1. «میانگین» [آمار، ریاضی] هم‌ارزِ «mean, mean value»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر چهارم. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۵۹-۱ (ذیل سرواژهٔ میانگین)
2. «میانگین‌گیری». دریافت‌شده در ۲ ژانویه ۲۰۱۱.