تحلیل رگرسیون

در مدل‌های آماری، تحلیل رگرسیون، تحلیل وایازشی[1] یا تحلیل ارتباط یک فرایند آماری برای تخمین روابط بین متغیرها می‌باشد. این روش شامل تکنیک‌های زیادی برای مدل‌سازی و تحلیل متغیرهای خاص و منحصر بفرد، با تمرکز بر رابطه بین متغیر وابسته و یک یا چند متغیر مستقل، می‌باشد. تحلیل رگرسیون خصوصاً کمک می‌کند در فهم اینکه چگونه مقدار متغیر وابسته با تغییر هرکدام از متغیرهای مستقل و با ثابت بودن دیگر متغیرهای مستقل تغییر می‌کند. بیشترین کاربرد تحلیل رگرسیون تخمین امید ریاضی شرطی متغیر وابسته از متغیرهای مستقل معین است که معادل مقدار متوسط متغیر وابسته است وقتی که متغیرهای مستقل ثابت هستند. کمترین کاربرد آن تمرکز روی چندک یا پارامتر مکانی توزیع شرطی متغیر وابسته از متغیر مستقل معین است. در همه موارد هدف تخمین یک تابع از متغیرهای مستقل است که تابع رگرسیون نامیده شده‌است. در تحلیل رگرسیون تعیین پراکندگی متغیر وابسته اطراف تابع رگرسیون مورد توجه است که می‌تواند توسط یک توزیع احتمال توضیح داده شود.

بخشی از مجموعه مباحث دربارهٔ آمار
تحلیل رگرسیون
مدل‌ها
رگرسیون خطی رگرسیون ساده خطی ‏(en)‏ رگرسیون چندجمله‌ای ‏(en)‏ رگرسیون چندمتغیره
مدل خطی تعمیم‌یافته انتخاب گسسته ‏(en)‏ رگرسیون لجستیک لوجیت چندجمله‌ای ‏(en)‏ لوجیت آمیخته ‏(en)‏ مدل پروبیت ‏(en)‏ پروبیت چندجمله‌ای ‏(en)‏ لوجیت مرتب ‏(en)‏ پروبیت مرتب ‏(en)‏ رگرسیون پواسون
مدل چندسطحی ‏(en)‏ مدل اثرهای ثابت ‏(en)‏ مدل اثرهای تصادفی ‏(en)‏ مدل آمیخته ‏(en)‏
رگرسیون غیرخطی ‏(en)‏ رگرسیون غیرپارامتریک ‏(en)‏ رگرسیون نیمه‌پارامتریک ‏(en)‏ رگرسیون باثبات رگرسیون چندک رگرسیون ایزوتونیک ‏(en)‏ رگرسیون مولفه اصلی رگرسیون کمترین زاویه رگرسیون موضعی ‏(en)‏ رگرسیون مقطع ‏(en)‏
مدل خطا در متغیرها ‏(en)‏
تخمین
کمترین مربعات کمترین مربعات خطی ‏(en)‏ کمترین مربعات غیرخطی ‏(en)‏
حداقل مربعات معمولی حداقل مربعات وزن‌دار ‏(en)‏ روش تعمیم‌یافته کمترین مربعات
رگرسیون پاره‌ای کمتری مربعات مجموع کمترین مربعات ‏(en)‏ کمترین مربعات نامنفی ‏(en)‏ تنظیم تیخونوف کمترین مربعات منظم ‏(en)‏
کمترین انحرافات مطلق ‏(en)‏ کمترین مربعات بازوزن‌داده مکرر ‏(en)‏ رگرسیون خطی بیزی رگرسیون چندمتغیره خطی بیزی
پیش‌زمینه
اعتبارسنجی مدل رگرسیون ‏(en)‏ پاسخ میانگین و پیش‌بینی‌شده ‏(en)‏ خطاها و باقی‌مانده‌ها در آمار ‏(en)‏ نیکویی برازش باقی‌مانده استودنت‌شده ‏(en)‏ قضیه گوس-مارکف
درگاه آمار

تحلیل رگرسیون به صورت گسترده برای پیش‌بینی استفاده شده‌است. تحلیل رگرسیون همچنین برای شناخت ارتباط میان متغیر مستقل و وابسته و شکل این روابط استفاده شده‌است. در شرایط خاصی این تحلیل برای استنتاج روابط عالی بین متغیرهای مستقل و وابسته می‌تواند استفاده شود. هرچند این می‌تواند موجب روابط اشتباه یا باطل شود بنابراین احتیاط قابل توصیه است.

تکنیک‌های زیادی برای انجام تحلیل رگرسیون توسعه داده شده‌است. روش‌های آشنا همچون رگرسیون خطی و حداقل مربعات که پارامتری هستند، در واقع در آن تابع رگرسیون تحت یک تعداد محدودی از پارامترهای ناشناخته از داده‌ها تخمین زده شده‌است. رگرسیون غیر پارامتری به روش‌هایی اشاره می‌کند که به توابع رگرسیون اجازه می‌دهد تا در یک مجموعه مشخص از توابع با احتمال پارامترهای نامحدود قرار گیرند.

تحلیل رگرسیونی یا تحلیل وایازشی فن و تکنیکی آماری برای بررسی و مدل‌سازی ارتباط بین متغیرها است. رگرسیون تقریباً در هر زمینه‌ای از جمله مهندسی، فیزیک، اقتصاد، مدیریت، علوم زیستی، بیولوژی و علوم اجتماعی برای برآورد و پیش‌بینی مورد نیاز است.

تعریف لغوی

در فرهنگ لغت واژه رگرسیون (Regression) از لحاظ لغوی به معنی پسروی، برگشت و بازگشت است. اما از دید آمار و ریاضیات به مفهوم بازگشت به یک مقدار متوسط یا میانگین به‌کارمی‌رود. بدین معنی که برخی پدیده‌ها به مرور زمان از نظر کمی به طرف یک مقدار متوسط میل می‌کنند.

تاریخچه

در سال ۱۸۷۷ فرانسیس گالتون (به انگلیسی: Francis Galton) در مقاله‌ای که دربارهٔ بازگشت به میانگین منتشر کرده‌بود، اظهار داشت که متوسط قد پسران دارای پدران قدبلند (کوتاه قد)، کمتر (بیشتر) از قد پدرانشان می‌باشد. به این ترتیب گالتون پدیده بازگشت به طرف میانگین را در داده‌هایش مورد تأکید قرارداد. برای گالتون رگرسیون مفهومی زیست‌شناختی داشت، اما کارهای او توسط کارل پیرسون (به انگلیسی: Karl Pearson) برای مفاهیم آماری توسعه داده‌شد. گرچه گالتون برای تأکید بر پدیده «بازگشت به سمت مقدار متوسط» از تحلیل رگرسیون استفاده کرد، اما به هر حال امروزه واژه تحلیل رگرسیون جهت اشاره به مطالعات مربوط به روابط بین متغیرها به کار برده‌می‌شود.[2]

مدل‌های رگرسیون

مدل‌های رگرسیون شامل متغیرهای زیر است:

• پارامترهای ناشناخته، با ${\displaystyle \beta }$ مشخص می‌شود و یک مقیاس یا بردار نمایش می‌دهد.
• متغیرهای مستقل ${\displaystyle X}$
• متغیر وابسته ${\displaystyle Y}$

در زمینه‌های مختلفی از کاربرد (زیست‌شناسی، علوم اجتماعی، اقتصاد، هوش مصنوعی و …)، اصطلاحات مختلفی به جای متغیرهای مستقل و وابسته استفاده شده‌است.

یک مدل رگرسیون، Y را به یک تابع از X و ${\displaystyle \beta }$ مرتبط می‌کند.

${\displaystyle Y\approx f(X,\beta )}$

نشان تقریب معمولاً به عنوان ${\displaystyle E(Y|X)=f(X,\beta )}$ معرفی شده‌است. برای انجام تحلیل رگرسیون، شکل تابع ${\displaystyle f}$ باید مشخص شده باشد. گاهی اوقات شکل این تابع بر اساس دانشی دربارهٔ روابط بین Y و X که بر روی داده تکیه ندارد.

فرض کنید بردار پارامترهای ناشناخته ${\displaystyle \beta }$ به طول k موجود است. برای اجرای یک تحلیل رگرسیون کاربر باید اطلاعاتی در مورد متغیر وابسته Y فراهم کند:

• اگر N نقطه داده از (Y,X)مشاهده شده باشد وقتی N<k است دیدگاه‌های بسیار کلاسیک برای این تحلیل نمی‌تواند استفاده شود از آنجایی که سیستم معادلات تعریف شده برای مدل رگرسیون قابل تخمین نیست و داده کافی برای بازیابی ${\displaystyle \beta }$ وجود ندارد.
• اگر تعداد نقاط N=k مشاهده شده‌است و تابع f خطی است، معادلات ${\displaystyle Y=f(X,\beta )}$ دقیق حل شود. این تعداد محاسبات به یک مجموعه N معادلات با N پارامتر ناشناخته (همان عناصر ${\displaystyle \beta }$)کاهش می‌دهد و یک راه حل یکتا دارد آنچنان که X متغیرهای مستقل خطی هستند. چندین راه حل شاید وجود داشته باشد اگر f غیرخطی است.
• وضعیت بسیار مشترک N>k است. در این صورت اطلاعات کافی در داده‌ها برای تخمین مقدار یکتا برای ${\displaystyle \beta }$ وجود دارد.

در مورد آخر، تحلیل رگرسیون ابزاری فراهم می‌کند:

1. یافتن یک راه حل برای پارامترهای ناشناخته ${\displaystyle \beta }$، برای نمونه فاصله بین مقادیر پیش‌بینی و اندازه‌گیری شده از متغیر مستقل Y حداقل کند (حداقل مربعات)
2. تحت فرض‌های آماری خاص، تحلیل رگرسیون اطلاعات زیادی برای تعیین اطلاعات آماری دربارهٔ پارامترهای ناشناخته ${\displaystyle \beta }$ و مقادیر پیش‌بینی از متغیر تصادفی Y استفاده می‌کند.

رگرسیون کاذب

رگرسیون کاذب (به انگلیسی: regression) با فرض اینکه متغیرهای ${\displaystyle y_{t}}$ و ${\displaystyle x_{t}}$ مانا می‌باشند تخمین‌های ما از پارامترها و تست‌های ${\displaystyle T}$و ${\displaystyle F}$درست می‌باشد. برای نشان‌دادن سازگاری تخمین‌های حداقل مربعات معمولی، ما از این نتایج زمانی که اندازه نمونه افزایش می‌یابد و واریانس نمونه به واریانس جامعه همگرا می‌شود، استفاده می‌کنیم. متأسفانه وقتی سری نامانا باشد واریانس خوش تعریف نیست، زیرا حول یک میانگین ثابت نوسان نمی‌کند. برای توضیح بیشتر دو متغیر ${\displaystyle y_{t}}$ و ${\displaystyle x_{t}}$ را در نظر بگیرید که به وسیلهٔ یک فرایند گام تصادفی تعریف می‌شود.

1. ${\displaystyle y_{t}=y_{t-1}+\epsilon _{1}t,\quad t=1,\dots ,N\!}$
2. ${\displaystyle x_{t}=x_{t-1}+\epsilon _{2}t,\quad t=1,\dots ,N\!}$

که ${\displaystyle \epsilon _{2}t}$ و ${\displaystyle \epsilon _{1}t}$ دارای توزیع مستقل می‌باشد. هیچ دلیلی برای ارتباط بین ${\displaystyle y_{t}}$ و ${\displaystyle x_{t}}$ وجود ندارد. یک محقق اگر اثر ${\displaystyle y_{t}}$ را روی ${\displaystyle x_{t}}$ و یک جزء ثابت رگرس کند و رگرسیون زیر را انجام دهد:

خط راست: ${\displaystyle y_{i}=\beta _{0}+\beta _{1}x_{t}+\epsilon _{t},\quad t=1,\dots ,N\!}$

نتایج این رگرسیون ممکن است به وسیلهٔ r^۲ بالا و خود همبستگی بالا بین باقیمانده‌ها و هم‌چنین دارای ارزش معنی‌داری برای پارامتر ${\displaystyle beta_{1}}$ باشد. این پدیده به رگرسیون کاذب معروف است. در این گونه از موارد دو سری نامانا ارتباط کاذبی دارند به این علت که که هر دوی آن‌ها در طول زمان تغییر می‌کنند و تابعی از زمانند. همان‌طور که گراجر و نی یو بلد بیان کردند در این حالت رگرسیون دارای r^۲ بالا؛ و آماره دوربین واتسون پایین خواهدبود و تست‌های ${\displaystyle T}$و ${\displaystyle F}$ ممکن است خیلی گمراه‌کننده باشند. دلیل آن نیز این است که توزیع‌های آماره‌های تست‌های سنتی خیلی متفاوت از نتایجی که تحت فرض مانایی گرفته‌می‌شود، می‌باشد. به‌خصوص همان‌طور که فلیپس (۱۹۸۷)نشان داد؛ همان‌طور که اندازه نمونه افزایش می‌یابد نمی‌توان به معنی‌داری تخمین زن حداقل مربعات معمولی و آماره‌های تست‌های ${\displaystyle T}$و ${\displaystyle F}$ و آماره دوربین واتسون اعتماد کرد. دلیل آن این است که ${\displaystyle y_{t}}$ و ${\displaystyle x_{t}}$ متغیرهای ${\displaystyle I(1)}$ می‌باشد و جزء خطا نیز یک متغیر نامانا${\displaystyle I(1)}$ می‌باشد.

اگر ارزش‌های گذشته هر دو متغیر وابسته و مستقل را در رگرسیون وارد کنیم مشکل رگرسیون کاذب حل می‌شود. در این حالت تخمین‌های حداقل مربعات معمولی برای همه پارامترها سازگار می‌باشد.

شیوه‌ها

شیوه‌های مهم تحلیل‌های رگرسیونی به شرج زیر هستند.

• رگرسیون خطی ساده
• رگرسیون خطی چندگانه
• رگرسیون فازی
• رگرسیون لجستیک

این تنوع باعث شده‌است که بتوان به راحتی هر نوع داده‌ای (اغلب از نوع داده‌های پیوسته) را تحلیل کرد و به راحتی نتیجه‌گیری نمود.

محاسبه

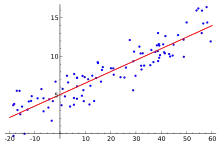
برای انجام یک تحلیل رگرسیونی ابتدا تحلیل‌گر حدس می‌زند که بین دو متغیر، نوعی ارتباط وجود دارد، در حقیقت حدس می‌زند که یک رابطه به شکل یک خط بین دو متغیر وجود دارد و سپس به جمع‌آوری اطلاعات کمی از دو متغیر می‌پردازد و این داده‌ها را به صورت نقاطی در یک نمودار دو بعدی رسم می‌کند.

نرم‌افزارها

نرم‌افزارهای بسیاری هستند که قابلیت محاسبه رگرسیون را دارند و مشهورترین آن‌ها عبارتند از:

• نرم‌افزار مایکروسافت اکسل (که ساده‌ترین نرم‌افزار است)
• اس‌پی‌اس‌اس SPSS
• اس‌پلاس +S یا Plus-S
• ساس (نرم‌افزار) SAS
• آر R

جستارهای وابسته

• تحلیل رگرسیون
• رگرسیون خطی
• رگرسیون لجستیک

منابع

1. «تحلیل وایازشی» [ریاضی] هم‌ارزِ «regression analysis» (انگلیسی)؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. (۱۳۷۶-۱۳۸۵). فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۷۷-۱ (ذیل سرواژهٔ تحلیل وایازشی)
2. بازرگان لاری، عبدالرضا (۱۳۹۱). رگرسیون خطی کاربردی. شیراز: انتشارات دانشگاه شیراز. شابک ۹۶۴-۴۶۲-۳۷۴-۶.