کمترین مربعات

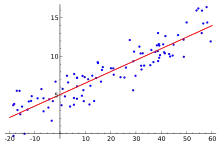
روش کمترین مربعات روشی در تحلیل رگرسیون است که برای حل دستگاه معادلاتی به کار می‌رود که تعداد معادله‌هایش بیش از تعداد مجهول‌هایش است. مهم‌ترین کاربرد روش کمترین مربعات در برازش منحنی بر داده‌ها است. مدل برازش شده بر داده‌ها، مدلی است که در آن کمیت ${\displaystyle \chi ^{2}}$ کمینه باشد.

${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-f({\vec {x_{i}}},{\vec {\beta }}))^{2}}{\sigma _{y,i}^{2}}}}$

بخشی از مجموعه مباحث دربارهٔ آمار
تحلیل رگرسیون
مدل‌ها
رگرسیون خطی رگرسیون ساده خطی ‏(en)‏ رگرسیون چندجمله‌ای ‏(en)‏ رگرسیون چندمتغیره
مدل خطی تعمیم‌یافته انتخاب گسسته ‏(en)‏ رگرسیون لجستیک لوجیت چندجمله‌ای ‏(en)‏ لوجیت آمیخته ‏(en)‏ مدل پروبیت ‏(en)‏ پروبیت چندجمله‌ای ‏(en)‏ لوجیت مرتب ‏(en)‏ پروبیت مرتب ‏(en)‏ رگرسیون پواسون
مدل چندسطحی ‏(en)‏ مدل اثرهای ثابت ‏(en)‏ مدل اثرهای تصادفی ‏(en)‏ مدل آمیخته ‏(en)‏
رگرسیون غیرخطی ‏(en)‏ رگرسیون غیرپارامتریک ‏(en)‏ رگرسیون نیمه‌پارامتریک ‏(en)‏ رگرسیون باثبات رگرسیون چندک رگرسیون ایزوتونیک ‏(en)‏ رگرسیون مولفه اصلی رگرسیون کمترین زاویه رگرسیون موضعی ‏(en)‏ رگرسیون مقطع ‏(en)‏
مدل خطا در متغیرها ‏(en)‏
تخمین
کمترین مربعات کمترین مربعات خطی ‏(en)‏ کمترین مربعات غیرخطی ‏(en)‏
حداقل مربعات معمولی حداقل مربعات وزن‌دار ‏(en)‏ روش تعمیم‌یافته کمترین مربعات
رگرسیون پاره‌ای کمتری مربعات مجموع کمترین مربعات ‏(en)‏ کمترین مربعات نامنفی ‏(en)‏ تنظیم تیخونوف کمترین مربعات منظم ‏(en)‏
کمترین انحرافات مطلق ‏(en)‏ کمترین مربعات بازوزن‌داده مکرر ‏(en)‏ رگرسیون خطی بیزی رگرسیون چندمتغیره خطی بیزی
پیش‌زمینه
اعتبارسنجی مدل رگرسیون ‏(en)‏ پاسخ میانگین و پیش‌بینی‌شده ‏(en)‏ خطاها و باقی‌مانده‌ها در آمار ‏(en)‏ نیکویی برازش باقی‌مانده استودنت‌شده ‏(en)‏ قضیه گوس-مارکف
درگاه آمار

برازش سهمی بر مجموعه‌ای از داده‌ها در نرم‌افزار اکسل

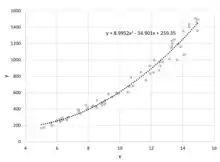
این روش را نخستین بار کارل فردریش گاوس در سال ۱۷۹۴ استفاده کرد.[1] روش کمترین مربعات در زبان برنامهٔ نویسی R، بیشتر نرم‌افزارهای آماری و ریاضی (مانند Excel, SPSS, MATLAB و …) و ماشین حساب‌های مهندسی وجود دارد.

تاریخچه

منشأ روش کمترین مربعات از نجوم و یافتن موقعیت ستارگان بوده‌است.

ساختار ریاضی

برای برازش منحنی ${\displaystyle y=f({\vec {x}})}$ بر داده‌ها، فرض می‌کنیم اندازه‌گیری‌ها مستقل از هم انجام شده‌اند و خطای ${\displaystyle {\vec {x}}}$ نیز در مقابل خطای ${\displaystyle y}$ قابل صرف نظر است (مقادیر ${\displaystyle {\vec {x}}}$ بدون خطا هستند). تابع ${\displaystyle f}$ علاوه بر ${\displaystyle {\vec {x}}}$، به ثوابتی که آن‌ها را با بردار ${\displaystyle {\vec {\beta }}}$ نشان می‌دهیم بستگی دارند. هدف، پیدا کردن مقادیر ${\displaystyle {\vec {\beta }}}$ است، به گونه‌ای که تابع ${\displaystyle f({\vec {x}},{\vec {\beta }})}$ دقیق‌ترین پیش‌بینی را از ${\displaystyle y}$ ارائه دهد. به این منظور، کمیت باقی مانده را به صورت

${\displaystyle d_{i}=y_{i}-f({\vec {x}}_{i},{\vec {\beta }})}$

تعریف می‌کنیم. اگر هر ${\displaystyle y_{i}}$ از توزیع نرمال حول مقدار واقعی ${\displaystyle f({\vec {x}}_{i},{\vec {\beta }})}$ با پهنای ${\displaystyle \sigma _{y,i}}$ پیروی کند، احتمال به دست آوردن ${\displaystyle y_{i}}$ متناسب است با:

${\displaystyle Prob_{\vec {\beta }}(y_{i})\propto {\frac {1}{\sigma _{y,i}^{2}}}e^{-d_{i}^{2}/2/\sigma _{y,i}^{2}}}$

است. احتمال مشاهدهٔ تمام مقادیر ${\displaystyle y}$ این‌طور به دست می‌آید:

${\displaystyle Prob_{\vec {\beta }}(y_{1},y_{2},...,y_{N})=Prob_{\vec {\beta }}(y_{1})\times Prob_{\vec {\beta }}(y_{2})\times ...\times Prob_{\vec {\beta }}(y_{N})}$

${\displaystyle \propto {\frac {1}{\prod _{i=1}^{N}\sigma _{y,i}}}e^{-\chi ^{2}/2}}$

کمیت ${\displaystyle \chi ^{2}}$ که در نما قرار دارد به صورت

${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-f({\vec {x_{i}}},{\vec {\beta }}))^{2}}{\sigma _{y,i}^{2}}}=\sum _{i=1}^{N}{\frac {d_{i}^{2}}{\sigma _{y,i}^{2}}}}$

تعریف می‌شود. پس هدف، پیدا کردن ${\displaystyle {\vec {\beta }}}$ است؛ به گونه‌ای که ${\displaystyle \chi ^{2}}$ کمینه شود.

${\displaystyle {\hat {\vec {\beta }}}=argmin_{\vec {\beta }}\,\,\chi ^{2}}$

برای بدست پارامتر بهینه باید از تابع مربعات گرادیان گرفته و آن را برابر با صفر قرار دهیم:[2]

${\displaystyle {\frac {\partial \chi ^{2}}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m,}$

کمترین مربعات بدون وزن

اگر فرض کنیم ${\displaystyle \sigma _{y,i}}$ها برای همهٔ داده‌ها برابر است، خواهیم داشت:

${\displaystyle 2\sum _{i}d_{i}{\frac {\partial d_{i}}{\partial \beta _{j}}}=-2\sum _{i}d_{i}{\frac {\partial f\left({\vec {x}}_{i},{\vec {\beta }}\right)}{\partial \beta _{j}}}=0,\ j=0,\ldots ,m}$

سایر روش‌ها

سایر انواع روش کمترین مربعات، عبارت‌اند از کمترین مربعات دارای قید (Constrained)، کمترین مربعات وزن‌دار (Weighted) و کمترین مربعات مجموع (Total)

نمونه‌ها

برازش خط

برای خط،

${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-A-Bx_{i})^{2}}{\sigma _{y}^{2}}}}$

با مشتق‌گیری جزئی، خواهیم داشت:

${\displaystyle {\frac {\partial \chi ^{2}}{\partial A}}={\frac {-2}{\sigma _{y}^{2}}}\sum _{i=1}^{N}{(y_{i}-A-Bx_{i})}=0\Rightarrow \ AN+B\sum \ x_{i}=\sum \ y_{i}}$

${\displaystyle {\frac {\partial \chi ^{2}}{\partial B}}={\frac {-2}{\sigma _{y}^{2}}}\sum _{i=1}^{N}{x_{i}(y_{i}-A-Bx_{i})}=0\Rightarrow \ A\sum \ x_{i}+B\sum \ x_{i}^{2}=\sum \ x_{i}y_{i}}$

در نتیجه:

${\displaystyle A={\bar {y}}-B{\bar {x}},B={\frac {\sum _{i=1}^{N}{y_{i}\ \left(x_{i}-{\bar {x}}\right)}}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}}$

برازش خط مبدأ گذر

با انجام محاسبات بالا برای خط مبدأ گذر خواهیم داشت:

${\displaystyle B={\frac {\sum _{i=1}^{N}{x_{i}y_{i}}}{\sum _{i=1}^{N}x_{i}^{2}}}}$

برازش سهمی

برای سهمی،

${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-A-Bx_{i}-Cx_{i}^{2})^{2}}{\sigma _{y}^{2}}}}$

در نهایت، دستگاه معادلات برازش چنین به دست می‌آید:[3]

${\displaystyle AN+B\sum x+C\sum x^{2}=\sum y}$

${\displaystyle A\sum x+B\sum x^{2}+C\sum x^{3}=\sum xy}$

${\displaystyle A\sum x^{2}+B\sum x^{3}+C\sum x^{4}=\sum x^{2}y}$

کمترین مربعات خطی

اگر فرض کنیم بُعد ورودی ${\displaystyle m}$ است، یعنی ${\displaystyle {\vec {x}}=[x_{1},x_{2},\dots ,x_{m}]}$ و تابع ${\displaystyle f(\,\cdot \,,{\vec {\beta }})}$ یک تابع خطی است، مسئله رگرسیون به یک مسئله بهینه‌سازی برای پیداکردن ${\displaystyle m+1}$ پارامتر تبدیل می‌شود. به این معنی که ما یک پارامتر چند متغیره به اسم ${\displaystyle {\vec {\beta }}=[\beta _{0},\beta _{1},\cdots ,\beta _{m}]}$ داریم و سعی می‌کنیم ${\displaystyle y}$ را با ترکیبی خطی از ${\displaystyle {\vec {x}}}$تخمین بزنیم یعنی ${\displaystyle f\left({\vec {x}},{\vec {\beta }}\right)=\beta _{0}+\sum _{i=1}^{m}\beta _{i}\times x_{i}}$. حال اگر یک بعد دیگر به متغیر ${\displaystyle {\vec {x}}}$ اضافه کنیم و مقدارش را همیشه عدد ثابت ${\displaystyle 1}$ در نظر بگیریم (${\displaystyle x_{0}=1}$) و ${\displaystyle {\vec {x}}}$ را به صورتِ ${\displaystyle {\vec {x}}=[1,x_{1},x_{2},\dots ,x_{m}]}$ تغییر دهیم، تخمینی که از ${\displaystyle y}$ داریم در واقع ضرب نقطه ای بردار ورودی و بردار پارامترهای ماست یعنی ${\displaystyle f\left({\vec {x}},{\vec {\beta }}\right)=\sum _{i=0}^{m}\beta _{i}\times x_{i}={\vec {\beta }}\,\,.\,{\vec {x}}}$. حال فرض کنیم که تعداد مثالهایی که قرار است برای تخمین پارامترها استفاده کنیم

${\displaystyle n}$ است و این مثالها را به این شکل نمایش دهیم ${\displaystyle D=({\vec {x_{1}}},y_{1}),\cdots ({\vec {x_{n}}},y_{n})}$. همان‌طور که در مقدمه گفتیم پارامتر بهینه پارامتری است که تابع ${\displaystyle S({\vec {\beta }})}$ را به حداقل برساند یعنی تابع پایین را:

${\displaystyle S({\vec {\beta }})=\sum _{i=1}^{n}r_{i}^{2}=\sum _{i=1}^{n}\left(y_{i}-f\left({\vec {x}}_{i},{\vec {\beta }}\right)\right)^{2}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}}$

از آنجا که تابع ${\displaystyle S\left({\vec {\beta }}\right)}$ نسبت به ${\displaystyle {\vec {\beta }}}$ تابعی کاملاً محدب است، در نقطه مینیمم گرادیان ما صفر خواهد بود و این روش پارامتر بهینه را بدست می‌دهد.[4] برای تسهیل کار شکل تابع را با بکارگیری چند ماتریس ساده می‌کنیم. دو ماتریس برای این کار نیاز داردیم ماتریس ${\displaystyle X}$ و ماتریس ${\displaystyle Y}$. ماتریس ${\displaystyle X}$ ماتریس ورودهای چندمتغیره ماست. هر سطر معادل یک نمونه از داده ماست، سطر ${\displaystyle i}$ام برابر است با ${\displaystyle i}$امین نمونه ورودی ما یعنی بردار ${\displaystyle {\vec {x_{i}}}}$، از اینرو ${\displaystyle X}$ یک ماتریس ${\displaystyle n\times (m+1)}$ خواهد بود. ماتریس ${\displaystyle Y}$ از طرف دیگر برابر است با مجموعه متغیرهای وابسته داده ما. سطر ${\displaystyle i}$ام این ماتریس برابر است با متغیر وابسته برای ${\displaystyle i}$امین نمونه داده ما یا همان ${\displaystyle y_{i}}$. ماتریس ${\displaystyle Y}$ یک ماتریس ${\displaystyle n\times 1}$ است. با کمک این دو ماتریس می‌توان تابع ضرر را به شکل ذیل تعریف کرد:

${\displaystyle L(D,{\vec {\beta }})=||X{\vec {\beta }}-Y||^{2}=(X{\vec {\beta }}-Y)^{T}(X{\vec {\beta }}-Y)=Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}}$

حال گرادیان این تابع را نسبت به ${\displaystyle {\vec {\beta }}}$ پیدا می‌کنیم که می‌شود:

${\displaystyle {\frac {\partial L(D,{\vec {\beta }})}{\partial {\vec {\beta }}}}={\frac {\partial \left(Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}\right)}{\partial {\vec {\beta }}}}=-2X^{T}Y+2X^{T}X{\vec {\beta }}}$

با برابر قرار دادن گرادیان با صفر پارامتر بهینه بدست می‌آید:

${\displaystyle -2X^{T}Y+2X^{T}X{\vec {\beta }}=0\Rightarrow X^{T}Y=X^{T}X{\vec {\beta }}\Rightarrow {\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y}$

پس پارامتر بهینه ما برابر است با:

${\displaystyle {\bf {{\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y}}}$

خطای روش کمترین مربعات

خطای برازش خط

خطای شیب و عرض از مبدأ خط برازش شده برابر است با (${\displaystyle d_{i}=y_{i}-(A+Bx_{i})}$):

${\displaystyle \left(\Delta A\right)^{2}\approx \left({\frac {1}{N}}+{\frac {{\bar {x}}^{2}}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}\right){\frac {\sum _{i=1}^{N}d_{i}^{2}}{N-2}},\left(\Delta B\right)^{2}\approx {\frac {1}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}{\frac {\sum _{i=1}^{N}d_{i}^{2}}{N-2}}}$

برای خط مبدأ گذر

${\displaystyle \left(\Delta B\right)^{2}\approx {\frac {1}{\sum _{i=1}^{N}x_{i}^{2}}}}$

پیاده‌سازی روش کمترین مربعات

زبان R

در زبان R، برازش تابع خطی به فرم

${\displaystyle y=m_{n}x_{n}+m_{n-1}x_{n-1}+...+m_{2}x_{2}+m_{1}x_{1}+b}$

بر داده‌ها به کمک تابع lsfit انجام می‌شود.[5] قطعه کدهای زیر، نحوهٔ پیاده‌سازی و خروجی را برای یک تابع ۲ متغیره نشان می‌دهد.

x = matrix(c(1.19, 1.08, 2.45, 2.53, 3.30, 2.97, 1.65, 0.58, 0.26, 4.39, 4.06, 0.55, 1.80, 1.68, 3.24, 2.23, 3.80, 4.63, 3.78, 4.84, # x_1 values
           1.60, 5.88, 1.55, 1.86, 1.06, 3.85, 9.29, 13.04, 14.52, 0.50, 2.89, 16.99, 15.42, 17.36, 11.82, 16.38, 11.06, 9.08, 17.75, 15.17), # x_2 values
           ncol = 2)
y = c(23.59, 31.95, 33.15, 34.00, 37.80, 41.07, 42.38, 43.76, 44.10, 44.16, 46.83, 50.52, 56.81, 59.04, 60.12, 61.84, 62.16, 64.18, 75.45, 76.77)
lsfit(x, y, intercept = TRUE)

خروجی کد

کمترین مربعات روش کمترین مربعات روشی در تحلیل رگرسیون است که برای حل دستگاه معادلاتی به کار می‌رود که تعداد معادله‌هایش بیش از تعداد مجهول‌هایش است. مهم‌ترین کاربرد روش کمترین مربعات در برازش منحنی بر داده‌ها است. مدل برازش شده بر داده‌ها، مدلی است که در آن کمیت ${\displaystyle \chi ^{2}}$ کمینه باشد. ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-f({\vec {x_{i}}},{\vec {\beta }}))^{2}}{\sigma _{y,i}^{2}}}}$ بخشی از مجموعه مباحث دربارهٔ آمار تحلیل رگرسیون مدل‌ها رگرسیون خطی رگرسیون ساده خطی ‏(en)‏ رگرسیون چندجمله‌ای ‏(en)‏ رگرسیون چندمتغیره مدل خطی تعمیم‌یافته انتخاب گسسته ‏(en)‏ رگرسیون لجستیک لوجیت چندجمله‌ای ‏(en)‏ لوجیت آمیخته ‏(en)‏ مدل پروبیت ‏(en)‏ پروبیت چندجمله‌ای ‏(en)‏ لوجیت مرتب ‏(en)‏ پروبیت مرتب ‏(en)‏ رگرسیون پواسون مدل چندسطحی ‏(en)‏ مدل اثرهای ثابت ‏(en)‏ مدل اثرهای تصادفی ‏(en)‏ مدل آمیخته ‏(en)‏ رگرسیون غیرخطی ‏(en)‏ رگرسیون غیرپارامتریک ‏(en)‏ رگرسیون نیمه‌پارامتریک ‏(en)‏ رگرسیون باثبات رگرسیون چندک رگرسیون ایزوتونیک ‏(en)‏ رگرسیون مولفه اصلی رگرسیون کمترین زاویه رگرسیون موضعی ‏(en)‏ رگرسیون مقطع ‏(en)‏ مدل خطا در متغیرها ‏(en)‏ تخمین کمترین مربعات کمترین مربعات خطی ‏(en)‏ کمترین مربعات غیرخطی ‏(en)‏ حداقل مربعات معمولی حداقل مربعات وزن‌دار ‏(en)‏ روش تعمیم‌یافته کمترین مربعات رگرسیون پاره‌ای کمتری مربعات مجموع کمترین مربعات ‏(en)‏ کمترین مربعات نامنفی ‏(en)‏ تنظیم تیخونوف کمترین مربعات منظم ‏(en)‏ کمترین انحرافات مطلق ‏(en)‏ کمترین مربعات بازوزن‌داده مکرر ‏(en)‏ رگرسیون خطی بیزی رگرسیون چندمتغیره خطی بیزی پیش‌زمینه اعتبارسنجی مدل رگرسیون ‏(en)‏ پاسخ میانگین و پیش‌بینی‌شده ‏(en)‏ خطاها و باقی‌مانده‌ها در آمار ‏(en)‏ نیکویی برازش باقی‌مانده استودنت‌شده ‏(en)‏ قضیه گوس-مارکف درگاه آمار برازش سهمی بر مجموعه‌ای از داده‌ها در نرم‌افزار اکسل این روش را نخستین بار کارل فردریش گاوس در سال ۱۷۹۴ استفاده کرد.[1] روش کمترین مربعات در زبان برنامهٔ نویسی R، بیشتر نرم‌افزارهای آماری و ریاضی (مانند Excel, SPSS, MATLAB و …) و ماشین حساب‌های مهندسی وجود دارد. تاریخچه منشأ روش کمترین مربعات از نجوم و یافتن موقعیت ستارگان بوده‌است. ساختار ریاضی برای برازش منحنی ${\displaystyle y=f({\vec {x}})}$ بر داده‌ها، فرض می‌کنیم اندازه‌گیری‌ها مستقل از هم انجام شده‌اند و خطای ${\displaystyle {\vec {x}}}$ نیز در مقابل خطای ${\displaystyle y}$ قابل صرف نظر است (مقادیر ${\displaystyle {\vec {x}}}$ بدون خطا هستند). تابع ${\displaystyle f}$ علاوه بر ${\displaystyle {\vec {x}}}$، به ثوابتی که آن‌ها را با بردار ${\displaystyle {\vec {\beta }}}$ نشان می‌دهیم بستگی دارند. هدف، پیدا کردن مقادیر ${\displaystyle {\vec {\beta }}}$ است، به گونه‌ای که تابع ${\displaystyle f({\vec {x}},{\vec {\beta }})}$ دقیق‌ترین پیش‌بینی را از ${\displaystyle y}$ ارائه دهد. به این منظور، کمیت باقی مانده را به صورت ${\displaystyle d_{i}=y_{i}-f({\vec {x}}_{i},{\vec {\beta }})}$ تعریف می‌کنیم. اگر هر ${\displaystyle y_{i}}$ از توزیع نرمال حول مقدار واقعی ${\displaystyle f({\vec {x}}_{i},{\vec {\beta }})}$ با پهنای ${\displaystyle \sigma _{y,i}}$ پیروی کند، احتمال به دست آوردن ${\displaystyle y_{i}}$ متناسب است با: ${\displaystyle Prob_{\vec {\beta }}(y_{i})\propto {\frac {1}{\sigma _{y,i}^{2}}}e^{-d_{i}^{2}/2/\sigma _{y,i}^{2}}}$ است. احتمال مشاهدهٔ تمام مقادیر ${\displaystyle y}$ این‌طور به دست می‌آید: ${\displaystyle Prob_{\vec {\beta }}(y_{1},y_{2},...,y_{N})=Prob_{\vec {\beta }}(y_{1})\times Prob_{\vec {\beta }}(y_{2})\times ...\times Prob_{\vec {\beta }}(y_{N})}$ ${\displaystyle \propto {\frac {1}{\prod _{i=1}^{N}\sigma _{y,i}}}e^{-\chi ^{2}/2}}$ کمیت ${\displaystyle \chi ^{2}}$ که در نما قرار دارد به صورت ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-f({\vec {x_{i}}},{\vec {\beta }}))^{2}}{\sigma _{y,i}^{2}}}=\sum _{i=1}^{N}{\frac {d_{i}^{2}}{\sigma _{y,i}^{2}}}}$ تعریف می‌شود. پس هدف، پیدا کردن ${\displaystyle {\vec {\beta }}}$ است؛ به گونه‌ای که ${\displaystyle \chi ^{2}}$ کمینه شود. ${\displaystyle {\hat {\vec {\beta }}}=argmin_{\vec {\beta }}\,\,\chi ^{2}}$ برای بدست پارامتر بهینه باید از تابع مربعات گرادیان گرفته و آن را برابر با صفر قرار دهیم:[2] ${\displaystyle {\frac {\partial \chi ^{2}}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m,}$ کمترین مربعات بدون وزن اگر فرض کنیم ${\displaystyle \sigma _{y,i}}$ها برای همهٔ داده‌ها برابر است، خواهیم داشت: ${\displaystyle 2\sum _{i}d_{i}{\frac {\partial d_{i}}{\partial \beta _{j}}}=-2\sum _{i}d_{i}{\frac {\partial f\left({\vec {x}}_{i},{\vec {\beta }}\right)}{\partial \beta _{j}}}=0,\ j=0,\ldots ,m}$ سایر روش‌ها سایر انواع روش کمترین مربعات، عبارت‌اند از کمترین مربعات دارای قید (Constrained)، کمترین مربعات وزن‌دار (Weighted) و کمترین مربعات مجموع (Total) نمونه‌ها برازش خط برای خط، ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-A-Bx_{i})^{2}}{\sigma _{y}^{2}}}}$ با مشتق‌گیری جزئی، خواهیم داشت: ${\displaystyle {\frac {\partial \chi ^{2}}{\partial A}}={\frac {-2}{\sigma _{y}^{2}}}\sum _{i=1}^{N}{(y_{i}-A-Bx_{i})}=0\Rightarrow \ AN+B\sum \ x_{i}=\sum \ y_{i}}$ ${\displaystyle {\frac {\partial \chi ^{2}}{\partial B}}={\frac {-2}{\sigma _{y}^{2}}}\sum _{i=1}^{N}{x_{i}(y_{i}-A-Bx_{i})}=0\Rightarrow \ A\sum \ x_{i}+B\sum \ x_{i}^{2}=\sum \ x_{i}y_{i}}$ در نتیجه: ${\displaystyle A={\bar {y}}-B{\bar {x}},B={\frac {\sum _{i=1}^{N}{y_{i}\ \left(x_{i}-{\bar {x}}\right)}}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}}$ برازش خط مبدأ گذر با انجام محاسبات بالا برای خط مبدأ گذر خواهیم داشت: ${\displaystyle B={\frac {\sum _{i=1}^{N}{x_{i}y_{i}}}{\sum _{i=1}^{N}x_{i}^{2}}}}$ برازش سهمی برای سهمی، ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-A-Bx_{i}-Cx_{i}^{2})^{2}}{\sigma _{y}^{2}}}}$ در نهایت، دستگاه معادلات برازش چنین به دست می‌آید:[3] ${\displaystyle AN+B\sum x+C\sum x^{2}=\sum y}$ ${\displaystyle A\sum x+B\sum x^{2}+C\sum x^{3}=\sum xy}$ ${\displaystyle A\sum x^{2}+B\sum x^{3}+C\sum x^{4}=\sum x^{2}y}$ کمترین مربعات خطی اگر فرض کنیم بُعد ورودی ${\displaystyle m}$ است، یعنی ${\displaystyle {\vec {x}}=[x_{1},x_{2},\dots ,x_{m}]}$ و تابع ${\displaystyle f(\,\cdot \,,{\vec {\beta }})}$ یک تابع خطی است، مسئله رگرسیون به یک مسئله بهینه‌سازی برای پیداکردن ${\displaystyle m+1}$ پارامتر تبدیل می‌شود. به این معنی که ما یک پارامتر چند متغیره به اسم ${\displaystyle {\vec {\beta }}=[\beta _{0},\beta _{1},\cdots ,\beta _{m}]}$ داریم و سعی می‌کنیم ${\displaystyle y}$ را با ترکیبی خطی از ${\displaystyle {\vec {x}}}$تخمین بزنیم یعنی ${\displaystyle f\left({\vec {x}},{\vec {\beta }}\right)=\beta _{0}+\sum _{i=1}^{m}\beta _{i}\times x_{i}}$. حال اگر یک بعد دیگر به متغیر ${\displaystyle {\vec {x}}}$ اضافه کنیم و مقدارش را همیشه عدد ثابت ${\displaystyle 1}$ در نظر بگیریم (${\displaystyle x_{0}=1}$) و ${\displaystyle {\vec {x}}}$ را به صورتِ ${\displaystyle {\vec {x}}=[1,x_{1},x_{2},\dots ,x_{m}]}$ تغییر دهیم، تخمینی که از ${\displaystyle y}$ داریم در واقع ضرب نقطه ای بردار ورودی و بردار پارامترهای ماست یعنی ${\displaystyle f\left({\vec {x}},{\vec {\beta }}\right)=\sum _{i=0}^{m}\beta _{i}\times x_{i}={\vec {\beta }}\,\,.\,{\vec {x}}}$. حال فرض کنیم که تعداد مثالهایی که قرار است برای تخمین پارامترها استفاده کنیم ${\displaystyle n}$ است و این مثالها را به این شکل نمایش دهیم ${\displaystyle D=({\vec {x_{1}}},y_{1}),\cdots ({\vec {x_{n}}},y_{n})}$. همان‌طور که در مقدمه گفتیم پارامتر بهینه پارامتری است که تابع ${\displaystyle S({\vec {\beta }})}$ را به حداقل برساند یعنی تابع پایین را: ${\displaystyle S({\vec {\beta }})=\sum _{i=1}^{n}r_{i}^{2}=\sum _{i=1}^{n}\left(y_{i}-f\left({\vec {x}}_{i},{\vec {\beta }}\right)\right)^{2}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}}$ از آنجا که تابع ${\displaystyle S\left({\vec {\beta }}\right)}$ نسبت به ${\displaystyle {\vec {\beta }}}$ تابعی کاملاً محدب است، در نقطه مینیمم گرادیان ما صفر خواهد بود و این روش پارامتر بهینه را بدست می‌دهد.[4] برای تسهیل کار شکل تابع را با بکارگیری چند ماتریس ساده می‌کنیم. دو ماتریس برای این کار نیاز داردیم ماتریس ${\displaystyle X}$ و ماتریس ${\displaystyle Y}$. ماتریس ${\displaystyle X}$ ماتریس ورودهای چندمتغیره ماست. هر سطر معادل یک نمونه از داده ماست، سطر ${\displaystyle i}$ام برابر است با ${\displaystyle i}$امین نمونه ورودی ما یعنی بردار ${\displaystyle {\vec {x_{i}}}}$، از اینرو ${\displaystyle X}$ یک ماتریس ${\displaystyle n\times (m+1)}$ خواهد بود. ماتریس ${\displaystyle Y}$ از طرف دیگر برابر است با مجموعه متغیرهای وابسته داده ما. سطر ${\displaystyle i}$ام این ماتریس برابر است با متغیر وابسته برای ${\displaystyle i}$امین نمونه داده ما یا همان ${\displaystyle y_{i}}$. ماتریس ${\displaystyle Y}$ یک ماتریس ${\displaystyle n\times 1}$ است. با کمک این دو ماتریس می‌توان تابع ضرر را به شکل ذیل تعریف کرد: ${\displaystyle L(D,{\vec {\beta }})=||X{\vec {\beta }}-Y||^{2}=(X{\vec {\beta }}-Y)^{T}(X{\vec {\beta }}-Y)=Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}}$ حال گرادیان این تابع را نسبت به ${\displaystyle {\vec {\beta }}}$ پیدا می‌کنیم که می‌شود: ${\displaystyle {\frac {\partial L(D,{\vec {\beta }})}{\partial {\vec {\beta }}}}={\frac {\partial \left(Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}\right)}{\partial {\vec {\beta }}}}=-2X^{T}Y+2X^{T}X{\vec {\beta }}}$ با برابر قرار دادن گرادیان با صفر پارامتر بهینه بدست می‌آید: ${\displaystyle -2X^{T}Y+2X^{T}X{\vec {\beta }}=0\Rightarrow X^{T}Y=X^{T}X{\vec {\beta }}\Rightarrow {\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y}$ پس پارامتر بهینه ما برابر است با: ${\displaystyle {\bf {{\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y}}}$ خطای روش کمترین مربعات خطای برازش خط خطای شیب و عرض از مبدأ خط برازش شده برابر است با (${\displaystyle d_{i}=y_{i}-(A+Bx_{i})}$): ${\displaystyle \left(\Delta A\right)^{2}\approx \left({\frac {1}{N}}+{\frac {{\bar {x}}^{2}}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}\right){\frac {\sum _{i=1}^{N}d_{i}^{2}}{N-2}},\left(\Delta B\right)^{2}\approx {\frac {1}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}{\frac {\sum _{i=1}^{N}d_{i}^{2}}{N-2}}}$ برای خط مبدأ گذر ${\displaystyle \left(\Delta B\right)^{2}\approx {\frac {1}{\sum _{i=1}^{N}x_{i}^{2}}}}$ پیاده‌سازی روش کمترین مربعات coefficients` Intercept X1 X2 12.288613 7.077099 2.046854 $residuals [1] -0.3953270240 -0.0173795577 0.3498706172 -0.0008219408 -0.0127054659 -0.1179842888 -0.6010969324 0.6756982152 0.2510266287 -0.2205056134 -0.1070429923 -0.4370605663 0.2201255541 -0.6715185403 0.7077756472 0.2419934166 [17] 0.3402088176 0.5389865978 0.0783001530 -0.8225427255 $intercept [1] TRUE $qr کمترین مربعات روش کمترین مربعات روشی در تحلیل رگرسیون است که برای حل دستگاه معادلاتی به کار می‌رود که تعداد معادله‌هایش بیش از تعداد مجهول‌هایش است. مهم‌ترین کاربرد روش کمترین مربعات در برازش منحنی بر داده‌ها است. مدل برازش شده بر داده‌ها، مدلی است که در آن کمیت ${\displaystyle \chi ^{2}}$ کمینه باشد. ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-f({\vec {x_{i}}},{\vec {\beta }}))^{2}}{\sigma _{y,i}^{2}}}}$ بخشی از مجموعه مباحث دربارهٔ آمار تحلیل رگرسیون مدل‌ها رگرسیون خطی رگرسیون ساده خطی ‏(en)‏ رگرسیون چندجمله‌ای ‏(en)‏ رگرسیون چندمتغیره مدل خطی تعمیم‌یافته انتخاب گسسته ‏(en)‏ رگرسیون لجستیک لوجیت چندجمله‌ای ‏(en)‏ لوجیت آمیخته ‏(en)‏ مدل پروبیت ‏(en)‏ پروبیت چندجمله‌ای ‏(en)‏ لوجیت مرتب ‏(en)‏ پروبیت مرتب ‏(en)‏ رگرسیون پواسون مدل چندسطحی ‏(en)‏ مدل اثرهای ثابت ‏(en)‏ مدل اثرهای تصادفی ‏(en)‏ مدل آمیخته ‏(en)‏ رگرسیون غیرخطی ‏(en)‏ رگرسیون غیرپارامتریک ‏(en)‏ رگرسیون نیمه‌پارامتریک ‏(en)‏ رگرسیون باثبات رگرسیون چندک رگرسیون ایزوتونیک ‏(en)‏ رگرسیون مولفه اصلی رگرسیون کمترین زاویه رگرسیون موضعی ‏(en)‏ رگرسیون مقطع ‏(en)‏ مدل خطا در متغیرها ‏(en)‏ تخمین کمترین مربعات کمترین مربعات خطی ‏(en)‏ کمترین مربعات غیرخطی ‏(en)‏ حداقل مربعات معمولی حداقل مربعات وزن‌دار ‏(en)‏ روش تعمیم‌یافته کمترین مربعات رگرسیون پاره‌ای کمتری مربعات مجموع کمترین مربعات ‏(en)‏ کمترین مربعات نامنفی ‏(en)‏ تنظیم تیخونوف کمترین مربعات منظم ‏(en)‏ کمترین انحرافات مطلق ‏(en)‏ کمترین مربعات بازوزن‌داده مکرر ‏(en)‏ رگرسیون خطی بیزی رگرسیون چندمتغیره خطی بیزی پیش‌زمینه اعتبارسنجی مدل رگرسیون ‏(en)‏ پاسخ میانگین و پیش‌بینی‌شده ‏(en)‏ خطاها و باقی‌مانده‌ها در آمار ‏(en)‏ نیکویی برازش باقی‌مانده استودنت‌شده ‏(en)‏ قضیه گوس-مارکف درگاه آمار برازش سهمی بر مجموعه‌ای از داده‌ها در نرم‌افزار اکسل این روش را نخستین بار کارل فردریش گاوس در سال ۱۷۹۴ استفاده کرد.[1] روش کمترین مربعات در زبان برنامهٔ نویسی R، بیشتر نرم‌افزارهای آماری و ریاضی (مانند Excel, SPSS, MATLAB و …) و ماشین حساب‌های مهندسی وجود دارد. تاریخچه منشأ روش کمترین مربعات از نجوم و یافتن موقعیت ستارگان بوده‌است. ساختار ریاضی برای برازش منحنی ${\displaystyle y=f({\vec {x}})}$ بر داده‌ها، فرض می‌کنیم اندازه‌گیری‌ها مستقل از هم انجام شده‌اند و خطای ${\displaystyle {\vec {x}}}$ نیز در مقابل خطای ${\displaystyle y}$ قابل صرف نظر است (مقادیر ${\displaystyle {\vec {x}}}$ بدون خطا هستند). تابع ${\displaystyle f}$ علاوه بر ${\displaystyle {\vec {x}}}$، به ثوابتی که آن‌ها را با بردار ${\displaystyle {\vec {\beta }}}$ نشان می‌دهیم بستگی دارند. هدف، پیدا کردن مقادیر ${\displaystyle {\vec {\beta }}}$ است، به گونه‌ای که تابع ${\displaystyle f({\vec {x}},{\vec {\beta }})}$ دقیق‌ترین پیش‌بینی را از ${\displaystyle y}$ ارائه دهد. به این منظور، کمیت باقی مانده را به صورت ${\displaystyle d_{i}=y_{i}-f({\vec {x}}_{i},{\vec {\beta }})}$ تعریف می‌کنیم. اگر هر ${\displaystyle y_{i}}$ از توزیع نرمال حول مقدار واقعی ${\displaystyle f({\vec {x}}_{i},{\vec {\beta }})}$ با پهنای ${\displaystyle \sigma _{y,i}}$ پیروی کند، احتمال به دست آوردن ${\displaystyle y_{i}}$ متناسب است با: ${\displaystyle Prob_{\vec {\beta }}(y_{i})\propto {\frac {1}{\sigma _{y,i}^{2}}}e^{-d_{i}^{2}/2/\sigma _{y,i}^{2}}}$ است. احتمال مشاهدهٔ تمام مقادیر ${\displaystyle y}$ این‌طور به دست می‌آید: ${\displaystyle Prob_{\vec {\beta }}(y_{1},y_{2},...,y_{N})=Prob_{\vec {\beta }}(y_{1})\times Prob_{\vec {\beta }}(y_{2})\times ...\times Prob_{\vec {\beta }}(y_{N})}$ ${\displaystyle \propto {\frac {1}{\prod _{i=1}^{N}\sigma _{y,i}}}e^{-\chi ^{2}/2}}$ کمیت ${\displaystyle \chi ^{2}}$ که در نما قرار دارد به صورت ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-f({\vec {x_{i}}},{\vec {\beta }}))^{2}}{\sigma _{y,i}^{2}}}=\sum _{i=1}^{N}{\frac {d_{i}^{2}}{\sigma _{y,i}^{2}}}}$ تعریف می‌شود. پس هدف، پیدا کردن ${\displaystyle {\vec {\beta }}}$ است؛ به گونه‌ای که ${\displaystyle \chi ^{2}}$ کمینه شود. ${\displaystyle {\hat {\vec {\beta }}}=argmin_{\vec {\beta }}\,\,\chi ^{2}}$ برای بدست پارامتر بهینه باید از تابع مربعات گرادیان گرفته و آن را برابر با صفر قرار دهیم:[2] ${\displaystyle {\frac {\partial \chi ^{2}}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m,}$ کمترین مربعات بدون وزن اگر فرض کنیم ${\displaystyle \sigma _{y,i}}$ها برای همهٔ داده‌ها برابر است، خواهیم داشت: ${\displaystyle 2\sum _{i}d_{i}{\frac {\partial d_{i}}{\partial \beta _{j}}}=-2\sum _{i}d_{i}{\frac {\partial f\left({\vec {x}}_{i},{\vec {\beta }}\right)}{\partial \beta _{j}}}=0,\ j=0,\ldots ,m}$ سایر روش‌ها سایر انواع روش کمترین مربعات، عبارت‌اند از کمترین مربعات دارای قید (Constrained)، کمترین مربعات وزن‌دار (Weighted) و کمترین مربعات مجموع (Total) نمونه‌ها برازش خط برای خط، ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-A-Bx_{i})^{2}}{\sigma _{y}^{2}}}}$ با مشتق‌گیری جزئی، خواهیم داشت: ${\displaystyle {\frac {\partial \chi ^{2}}{\partial A}}={\frac {-2}{\sigma _{y}^{2}}}\sum _{i=1}^{N}{(y_{i}-A-Bx_{i})}=0\Rightarrow \ AN+B\sum \ x_{i}=\sum \ y_{i}}$ ${\displaystyle {\frac {\partial \chi ^{2}}{\partial B}}={\frac {-2}{\sigma _{y}^{2}}}\sum _{i=1}^{N}{x_{i}(y_{i}-A-Bx_{i})}=0\Rightarrow \ A\sum \ x_{i}+B\sum \ x_{i}^{2}=\sum \ x_{i}y_{i}}$ در نتیجه: ${\displaystyle A={\bar {y}}-B{\bar {x}},B={\frac {\sum _{i=1}^{N}{y_{i}\ \left(x_{i}-{\bar {x}}\right)}}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}}$ برازش خط مبدأ گذر با انجام محاسبات بالا برای خط مبدأ گذر خواهیم داشت: ${\displaystyle B={\frac {\sum _{i=1}^{N}{x_{i}y_{i}}}{\sum _{i=1}^{N}x_{i}^{2}}}}$ برازش سهمی برای سهمی، ${\displaystyle \chi ^{2}=\sum _{i=1}^{N}{\frac {(y_{i}-A-Bx_{i}-Cx_{i}^{2})^{2}}{\sigma _{y}^{2}}}}$ در نهایت، دستگاه معادلات برازش چنین به دست می‌آید:[3] ${\displaystyle AN+B\sum x+C\sum x^{2}=\sum y}$ ${\displaystyle A\sum x+B\sum x^{2}+C\sum x^{3}=\sum xy}$ ${\displaystyle A\sum x^{2}+B\sum x^{3}+C\sum x^{4}=\sum x^{2}y}$ کمترین مربعات خطی اگر فرض کنیم بُعد ورودی ${\displaystyle m}$ است، یعنی ${\displaystyle {\vec {x}}=[x_{1},x_{2},\dots ,x_{m}]}$ و تابع ${\displaystyle f(\,\cdot \,,{\vec {\beta }})}$ یک تابع خطی است، مسئله رگرسیون به یک مسئله بهینه‌سازی برای پیداکردن ${\displaystyle m+1}$ پارامتر تبدیل می‌شود. به این معنی که ما یک پارامتر چند متغیره به اسم ${\displaystyle {\vec {\beta }}=[\beta _{0},\beta _{1},\cdots ,\beta _{m}]}$ داریم و سعی می‌کنیم ${\displaystyle y}$ را با ترکیبی خطی از ${\displaystyle {\vec {x}}}$تخمین بزنیم یعنی ${\displaystyle f\left({\vec {x}},{\vec {\beta }}\right)=\beta _{0}+\sum _{i=1}^{m}\beta _{i}\times x_{i}}$. حال اگر یک بعد دیگر به متغیر ${\displaystyle {\vec {x}}}$ اضافه کنیم و مقدارش را همیشه عدد ثابت ${\displaystyle 1}$ در نظر بگیریم (${\displaystyle x_{0}=1}$) و ${\displaystyle {\vec {x}}}$ را به صورتِ ${\displaystyle {\vec {x}}=[1,x_{1},x_{2},\dots ,x_{m}]}$ تغییر دهیم، تخمینی که از ${\displaystyle y}$ داریم در واقع ضرب نقطه ای بردار ورودی و بردار پارامترهای ماست یعنی ${\displaystyle f\left({\vec {x}},{\vec {\beta }}\right)=\sum _{i=0}^{m}\beta _{i}\times x_{i}={\vec {\beta }}\,\,.\,{\vec {x}}}$. حال فرض کنیم که تعداد مثالهایی که قرار است برای تخمین پارامترها استفاده کنیم ${\displaystyle n}$ است و این مثالها را به این شکل نمایش دهیم ${\displaystyle D=({\vec {x_{1}}},y_{1}),\cdots ({\vec {x_{n}}},y_{n})}$. همان‌طور که در مقدمه گفتیم پارامتر بهینه پارامتری است که تابع ${\displaystyle S({\vec {\beta }})}$ را به حداقل برساند یعنی تابع پایین را: ${\displaystyle S({\vec {\beta }})=\sum _{i=1}^{n}r_{i}^{2}=\sum _{i=1}^{n}\left(y_{i}-f\left({\vec {x}}_{i},{\vec {\beta }}\right)\right)^{2}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}}$ از آنجا که تابع ${\displaystyle S\left({\vec {\beta }}\right)}$ نسبت به ${\displaystyle {\vec {\beta }}}$ تابعی کاملاً محدب است، در نقطه مینیمم گرادیان ما صفر خواهد بود و این روش پارامتر بهینه را بدست می‌دهد.[4] برای تسهیل کار شکل تابع را با بکارگیری چند ماتریس ساده می‌کنیم. دو ماتریس برای این کار نیاز داردیم ماتریس ${\displaystyle X}$ و ماتریس ${\displaystyle Y}$. ماتریس ${\displaystyle X}$ ماتریس ورودهای چندمتغیره ماست. هر سطر معادل یک نمونه از داده ماست، سطر ${\displaystyle i}$ام برابر است با ${\displaystyle i}$امین نمونه ورودی ما یعنی بردار ${\displaystyle {\vec {x_{i}}}}$، از اینرو ${\displaystyle X}$ یک ماتریس ${\displaystyle n\times (m+1)}$ خواهد بود. ماتریس ${\displaystyle Y}$ از طرف دیگر برابر است با مجموعه متغیرهای وابسته داده ما. سطر ${\displaystyle i}$ام این ماتریس برابر است با متغیر وابسته برای ${\displaystyle i}$امین نمونه داده ما یا همان ${\displaystyle y_{i}}$. ماتریس ${\displaystyle Y}$ یک ماتریس ${\displaystyle n\times 1}$ است. با کمک این دو ماتریس می‌توان تابع ضرر را به شکل ذیل تعریف کرد: ${\displaystyle L(D,{\vec {\beta }})=||X{\vec {\beta }}-Y||^{2}=(X{\vec {\beta }}-Y)^{T}(X{\vec {\beta }}-Y)=Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}}$ حال گرادیان این تابع را نسبت به ${\displaystyle {\vec {\beta }}}$ پیدا می‌کنیم که می‌شود: ${\displaystyle {\frac {\partial L(D,{\vec {\beta }})}{\partial {\vec {\beta }}}}={\frac {\partial \left(Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }}\right)}{\partial {\vec {\beta }}}}=-2X^{T}Y+2X^{T}X{\vec {\beta }}}$ با برابر قرار دادن گرادیان با صفر پارامتر بهینه بدست می‌آید: ${\displaystyle -2X^{T}Y+2X^{T}X{\vec {\beta }}=0\Rightarrow X^{T}Y=X^{T}X{\vec {\beta }}\Rightarrow {\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y}$ پس پارامتر بهینه ما برابر است با: ${\displaystyle {\bf {{\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y}}}$ خطای روش کمترین مربعات خطای برازش خط خطای شیب و عرض از مبدأ خط برازش شده برابر است با (${\displaystyle d_{i}=y_{i}-(A+Bx_{i})}$): ${\displaystyle \left(\Delta A\right)^{2}\approx \left({\frac {1}{N}}+{\frac {{\bar {x}}^{2}}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}\right){\frac {\sum _{i=1}^{N}d_{i}^{2}}{N-2}},\left(\Delta B\right)^{2}\approx {\frac {1}{\sum _{i=1}^{N}\left(x_{i}-{\bar {x}}\right)^{2}}}{\frac {\sum _{i=1}^{N}d_{i}^{2}}{N-2}}}$ برای خط مبدأ گذر ${\displaystyle \left(\Delta B\right)^{2}\approx {\frac {1}{\sum _{i=1}^{N}x_{i}^{2}}}}$

نرم‌افزار Excel

در نرم‌افزار اکسل، برازش تابع خطی به فرم

${\displaystyle y=m_{n}x_{n}+m_{n-1}x_{n-1}+...+m_{2}x_{2}+m_{1}x_{1}+b}$

بر داده‌ها به کمک تابع LINEST انجام می‌شود.[6] این تابع جزو توابع آرایه‌ای است و با فشردن Ctrl+Enter اجرا می‌شود. ورودی تابع به شکل

LINEST(known_y's, [known_x's], [const], [stats])

است که در آن به ترتیب مقادیر y، مقادیر x و سپس دو مقدار بولی وارد می‌شوند که اولی برای مبدأ گذر نبودن و دومی برای بازگرداندن مقادیر خطا، رگرسیون و … است. خروجی تابع در جدولی به صورت زیر برگردانده می‌شود:

جدول مقادیر بازگردانده شده

F	E	D	C	B	A
${\displaystyle b}$	${\displaystyle m_{1}}$	${\displaystyle m_{2}}$	...	${\displaystyle m_{n-1}}$	${\displaystyle m_{n}}$
${\displaystyle {se}_{b}}$	${\displaystyle {se}_{1}}$	${\displaystyle {se}_{2}}$	...	${\displaystyle {se}_{n-1}}$	${\displaystyle {se}_{n}}$
				${\displaystyle {se}_{y}}$	${\displaystyle r_{2}}$
				${\displaystyle d_{f}}$	${\displaystyle F}$
				${\displaystyle {ss}_{resid}}$	${\displaystyle {ss}_{reg}}$

منظور از ${\displaystyle {se}}$ خطا است. خانه‌های ردیف دوم به بعد، در صورتی نشان داده می‌شوند که stats=TRUE باشد.

ماشین حساب CASIO fx-82ES

اکثر ماشین حساب‌های مهندسی مجهز به ویژگی برازش منحنی به روش کمترین مربعات هستند. در ماشین حساب‌های کاسیو این ویژگی در بخش STAT قرار دارد.

لاسو (LASSO)

لاسو یک مدل تنظیم شده (به انگلیسی: Regularized) از مدل کمترین مربعات است. تنظیم به این صورت است که ${\displaystyle \|\beta \|^{1}}$ یا نرم L¹-norm کمتر از مقدار مشخصی باشد. این معادل این است که در هنگام بهینه‌سازی هزینهٔ کمترین مربعات ${\displaystyle \alpha \|\beta \|^{1}}$ را نیز اضافه کرده باشیم. معادل بیزی این مدل این است که توزیع پیشین توزیع لاپلاس را برای پارامترهای مدل خطی استفاده کرده باشیم.

تفاوت اساسی بین مدل ridge regression و لاسو این است که در اولی علی‌رغم افزایش جریمه، ضرایب در عین غیرصفر بودن کوچکتر می‌شوند، علی‌رغم اینکه صفر نمی‌شوند، در صورتی که در لاسو با افزایش جریمه، تعداد بسیار بیشتری از ضرایب به سمت صفر میل می‌کنند.[7] می‌توان بهینه‌سازی مربوط به لاسو را با روش‌های بهینه‌سازی درجه دوم یا در حالت کلی بهینه‌سازی محدب انجام داد. به دلیل ایجاد ضرایب کم، لاسو در بسیاری از کاربردها مانند سنجش فشرده (به انگلیسی: compressed sensing) مورد استفاده قرار می‌گیرد.

لاسو در رگرسیون خطی

پیچیدگی مدلهای پارامتری با تعداد پارامترهای مدل و مقادیر آن‌ها سنجیده می‌شود. هرچه این پیچیدگی بیشتر باشد خطر بیش‌برازش (Overfitting) برای مدل بیشتر است.[8] پدیده بیش‌برازش زمانی رخ می‌دهد که مدل بجای یادگیری الگوهای داده، داده را را حفظ می‌کند و در عمل یادگیری به خوبی انجام نمی‌شود. برای جلوگیری از بیش‌برازش در مدلهای خطی مانند رگرسیون خطی جریمه‌ای به تابع هزینه اضافه می‌شود تا از افزایش زیاد پارامترها جلوگیری شود. به این کار تنظیم مدل یا Regularization گفته می‌شود.[9] یکی از این روشهای تنظیم مدل روش لاسو است که در آن ضریبی از نُرمِ ${\displaystyle L_{1}}$به تابع هزینه اضافه می‌شود، در رگرسیون خطی تابع هزینه به شکل پایین تغییر می‌کند:

${\displaystyle L_{r}(D,{\vec {\beta }})=L(D,{\vec {\beta }})+\lambda ||{\vec {\beta }}||_{1}=\sum _{i=1}^{n}({\vec {\beta }}\,.\,{\vec {x_{i}}}-y_{i})^{2}+\lambda \sum _{k=0}^{m}|\beta _{k}|}$

این روش تنظیم مدل باعث می‌شود که بسیاری از پارامترهای مدل نهائی صفر شوند و مدل به اصلاح خلوت (Sparse) شود.[7]

جستارهای وابسته

• کمینه مربعات خطی
• رگرسیون خطی
• رگرسیون لجیستیک
• رگرسیون پواسون

پانویس

1. Bretscher, Otto (1995), Linear Algebra With Applications, 3rd ed., Upper Saddle River NJ: Prentice Hall
2. Yan, Xin (2009). Linear Regression Analysis: Theory and Computing. World Scientific. ISBN 9789812834119.
3. Taylor, John (1997). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed. University Science Books. ISBN 9780935702750.
4. Rencher, Alvin C.; Christensen, William F. (2012-08-15). Methods of Multivariate Analysis (به English). John Wiley & Sons. p. 155. ISBN 9781118391679.
5. https://stat.ethz.ch/R-manual/R-devel/RHOME/library/stats/html/lsfit.html The R manual: lsfit function LINEST function
6. https://support.office.com/en-us/article/linest-function-84d7d0d9-6e50-4101-977a-fa7abf772b6d Microsoft Office Excel Help: LINEST function
7. Natarajan, B. K. (1995). "Sparse Approximate Solutions to Linear Systems". SIAM Journal on Computing. 24 (2): 227–234. doi:10.1137/s0097539792240406. ISSN 0097-5397.
8. Bühlmann, Peter; van de Geer, Sara (2011). "Statistics for High-Dimensional Data". Springer Series in Statistics. doi:10.1007/978-3-642-20192-9. ISSN 0172-7397.
9. Bühlmann, Peter; van de Geer, Sara (2011). Theory for ℓ1/ℓ2-penalty procedures. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 249–291. doi:10.1007/978-3-642-20192-9_8. ISBN 9783642201912.