رگرسیون لجستیک
رگرسیون لجستیک (به انگلیسی: Logistic regression) یک مدل آماری رگرسیون برای متغیرهای وابسته دوسویی مانند بیماری یا سلامت، مرگ یا زندگی است. این مدل را میتوان به عنوان مدل خطی تعمیمیافتهای که از تابع لوجیت به عنوان تابع پیوند استفاده میکند و خطایش از توزیع چندجملهای پیروی میکند، بهحسابآورد. منظور از دو سویی بودن، رخ داد یک واقعه تصادفی در دو موقعیت ممکنه است. به عنوان مثال خرید یا عدم خرید، ثبت نام یا عدم ثبت نام، ورشکسته شدن یا ورشکسته نشدن و … متغیرهایی هستند که فقط دارای دو موقعیت هستند و مجموع احتمال هر یک آنها در نهایت یک خواهد شد. کاربرد این روش عمدتاً در ابتدای ظهور در مورد کاربردهای پزشکی برای احتمال وقوع یک بیماری مورد استفاده قرار میگرفت. لیکن امروزه در تمام زمینههای علمی کاربرد وسیعی یافتهاست. به عنوان مثال مدیر سازمانی میخواهد بداند در مشارکت یا عدم مشارکت کارمندان کدام متغیرها نقش پیشبینی دارند؟ مدیر تبلیغاتی میخواهد بداند در خرید یا عدم خرید یک محصول یا برند چه متغیرهایی مهم هستند؟ یک مرکز تحقیقات پزشکی میخواهد بداند در مبتلا شدن به بیماری عروق کرنری قلب چه متغیرهایی نقش پیشبینیکننده دارند؟ تا با اطلاعرسانی از احتمال وقوع کاسته شود.
| بخشی از مجموعه مباحث دربارهٔ آمار |
| تحلیل رگرسیون |
|---|
 |
| مدلها |
|
|
|
|
| تخمین |
|
|
|
|
| پیشزمینه |
|
|
رگرسیون لجستیک میتواند یک مورد خاص از مدل خطی عمومی و رگرسیون خطی دیده شود. مدل رگرسیون لجستیک، بر اساس فرضهای کاملاً متفاوتی (دربارهٔ رابطه متغیرهای وابسته و مستقل) از رگرسیون خطی است. تفاوت مهم این دو مدل در دو ویژگی رگرسیون لجستیک میتواند دیده شود. اول توزیع شرطی یک توزیع برنولی به جای یک توزیع گوسی است چونکه متغیر وابسته دودویی است. دوم مقادیر پیشبینی احتمالاتی است و محدود بین بازه صفر و یک و به کمک تابع توزیع لجستیک بدست میآید رگرسیون لجستیک احتمال خروجی پیشبینی میکند.
این مدل به صورت
است که
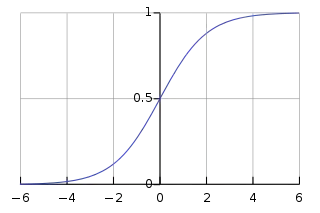
رگرسیون لجستیک را میتوان توسط تابع لجستیک تعریف کرد. دامنه این تابع اعداد حقیقی هستند و برد این تابع بین صفر و یک میباشد.[1] این تابع با نمایش داده میشود و به نحو پایین محاسبه میشود:[1]
با احتساب تابع لجستیک، رگرسیون لجستیک را میتوان به شکل پایین بازنویسی کرد:[1]
برآورد پارامترهای بهینه
برای بدست آوردن پارامترهای بهینه یعنی میتوان از روش برآورد درست نمایی بیشینه (Maximum Likelihood Estimation) استفاده کرد. اگر فرض کنیم که تعداد مثالهایی که قرار است برای تخمین پارامترها استفاده کنیم است و این مثالها را به این شکل نمایش دهیم . پارامتر بهینه پارامتری است که برآورد درست نمایی را بیشینه کند، البته برای سادگی کار برآورد لگاریتم درست نمایی را بیشینه میکنیم. لگاریتم درست نمایی داده برای پارامتر را با نمایش میدهیم:
اگر برای داده ام باشد، هدف افزایش است و اگر صفر باشد هدف افزایش مقدار است. از این رو از فرمول استفاده میکنیم که اگر باشد، فرمول به ما را بدهد و اگر بود به ما را بدهد.
حال برای بدست آوردن پارامتر بهینه باید یی پیدا کنیم که مقدار را بیشینه کند. از آنجا که این تابع نسبت به مقعر است حتماً یک بیشینه مطلق دارد. برای پیدا کردن جواب میتوان از روش گرادیان افزایشی از نوع تصادفی اش استفاده کرد (Stochastic Gradient Ascent). در این روش هر بار یک مثال را بهصورت اتفاقی از نمونههای داده انتخاب کرده، گرادیان درست نمایی را حساب میکنیم و کمی در جهت گرادیان پارامتر را حرکت میدهیم تا به یک پارامتر جدید برسیم. گرادیان جهت موضعی بیشترین افزایش را در تابع به ما نشان میدهد، برای همین در آن جهت کمی حرکت میکنیم تا به بیشترین افزایش موضعی تابع برسیم. اینکار را آنقدر ادامه میدهیم که گرادیان به اندازه کافی به صفر نزدیک شود. بهجای اینکه دادهها را بهصورت تصادفی انتخاب کنیم میتوانیم به ترتیب داده شماره تا داده شماره را انتخاب کنیم و بعد دوباره به داده اولی برگردیم و این کار را بهصورت متناوب چندین بار انجام دهیم تا به اندازه کافی گرادیان به صفر نزدیک شود. از لحاظ ریاضی این کار را میتوان به شکل پایین انجام داد، پارامتر را در ابتدا بهصورت تصادفی مقدار دهی میکنیم و بعد برای داده ام و تمامی ها، یعنی از تا تغییر پایین را اعمال میکنیم، دراینجا همان مقداریست که در جهت گرادیان هربار حرکت میکنیم و مشتق جزئی داده ام در بُعد ام است:
تنظیم مدل (Regularization)
پیچیدگی مدلهای پارامتری با تعداد پارامترهای مدل و مقادیر آنها سنجیده میشود. هرچه این پیچیدگی بیشتر باشد خطر بیشبرازش (Overfitting) برای مدل بیشتر است.[2] پدیده بیشبرازش زمانی رخ میدهد که مدل بهجای یادگیری الگوهای داده، داده را را حفظ کند و در عمل، فرایند یادگیری به خوبی انجام نمیشود. برای جلوگیری از بیشبرازش در مدلهای خطی مانند رگرسیون خطی یا رگرسیون لجستیک جریمهای به تابع هزینه اضافه میشود تا از افزایش زیاد پارامترها جلوگیری شود. تابع هزینه را در رگرسیون لجستیک با منفی لگاریتم درستنمایی تعریف میکنیم تا کمینه کردن آن به بیشینه کردن تابع درست نمایی بیانجامد. به این کار تنظیم مدل یا Regularization گفته میشود. دو راه متداول تنظیم مدلهای خطی روشهای و هستند.[3] در روش ضریبی از نُرمِ به تابع هزینه اضافه میشود و در روش ضریبی از نُرمِ که همان نُرمِ اقلیدسی است به تابع هزینه اضافه میشود.
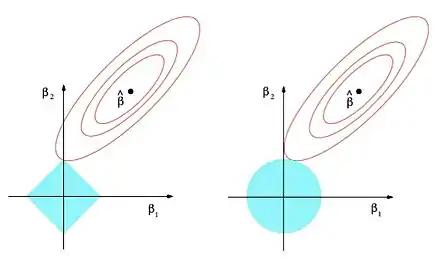
در تنظیم مدل به روش تابع هزینه را به این شکل تغییر میدهیم:[5]
این روش تنظیم مدل که به روش لاسو (Lasso) نیز شهرت دارد باعث میشود که بسیاری از پارامترهای مدل نهائی صفر شوند و مدل به اصطلاح خلوت (Sparse) شود.[6]
در تنظیم مدل به روش تابع هزینه را به این شکل تغییر میدهیم:
در روش تنظیم از طریق سعی میشود طول اقلیدسی بردار کوتاه نگه داشته شود. در روش و یک عدد مثبت است که میزان تنظیم مدل را معین میکند. هرچقدر کوچکتر باشد جریمه کمتری برا بزرگی نرم بردار پارامترها یعنی پرداخت میکنیم. مقدار ایدئال از طریق آزمایش بر روی داده اعتبار (Validation Data) پیدا میشود.
تفسیر احتمالی تنظیم مدل
اگر بهجای روش درست نمایی بیشینه از روش بیشینه سازی احتمال پسین استفاده کنیم به ساختار «تنظیم مدل» یا همان regularization خواهیم رسید.[7] اگر مجموعه داده را با نمایش بدهیم و پارامتری که به دنبال تخمین آن هستیم را با ، احتمال پسین ، طبق قانون بیز متناسب خواهد بود با حاصلضرب درست نمایی یعنی و احتمال پیشین یعنی :[8]
ازین رو
معادله خط پیشین نشان میدهد که برای یافتن پارامتر بهینه فقط کافیست که احتمال پیشین را نیز در معادله دخیل کنیم. اگر احتمال پیشین را یک توزیع احتمال با میانگین صفر و کوواریانس در نظر بگیریم به معادله پایین میرسیم:[8]
با ساده کردن این معادله به نتیجه پایین میرسیم:
با تغییر علامت معادله، بیشینهسازی را به کمینهسازی تغییر میدهیم، در این معادله همان است:
همانطور که دیدیم جواب همان تنظیم مدل با نرم است.
حال اگر توزیع پیشین را از نوع توزیع لاپلاس با میانگین صفر در نظر بگیریم به تنظیم مدل با نرم خواهیم رسید.[8]
از آنجا که میانگین هر دو توزیع پیشین صفر است، پیشفرض تخمین پارامتر بر این بنا شدهاست که اندازه پارامتر مورد نظر کوچک و به صفر نزدیک باشد و این پیشفرض با روند تنظیم مدل همخوانی دارد.[8]
کاربردها
رگرسیون لجستیک در زمینههای مختلف از جمله یادگیری ماشین، اکثر رشتههای پزشکی و علوم اجتماعی مورد استفاده قرار میگیرد. به عنوان مثال، میزان آسیبدیدگی (به انگلیسی: TRISS)، که بهطور گسترده برای پیشبینی مرگ و میر در بیماران مصدوم مورد استفاده قرار میگیرد، توسط بوید و همکارانش با استفاده از رگرسیون لجستیک ایجاد شد.[9] مقیاسهای پزشکی دیگری که برای ارزیابی شدت بیماری به کار میرود با استفاده از رگرسیون لجستیک ساخته شدهاند.[10][11][12][13] رگرسیون لجستیک ممکن است برای پیشبینی خطر ابتلا به یک بیماری خاص (به عنوان مثال دیابت؛ بیماری انسداد قلب)، بر اساس ویژگیهای مشاهده شده بیمار (سن، جنس، شاخص توده بدنی، نتایج آزمایشهای مختلف خون و غیره) مورد استفاده قرار گیرد.[14][15] رگرسیون لجستیک در علوم سیاسی هم کاربرد دارد. به عنوان مثال این مدل میتواند بر روی پیشبینی اینکه رایدهنده نپالی به کنگره نپالی یا حزب کمونیست نپال یا هر حزب دیگری رای دهد، بر اساس سن، درآمد، جنس، نژاد، وضعیت سکونت، آراء در انتخاباتهای قبلی و غیره کارکند.[16] این روش همچنین میتواند در مهندسی مورد استفاده قرار گیرد، به ویژه برای پیشبینی احتمال عدم موفقیت یک فرایند، سیستم یا محصول معین.[17][18] همچنین در برنامههای بازاریابی مانند پیشبینی تمایل مشتری برای خرید یک محصول یا متوقف کردن اشتراک و غیره مورد استفاده قرار گیرد.[19]
تاریخچه
تابع لجستیک به عنوان مدلی برای پیشبینی رشد جمعیت توسط پیر فرانسوا ورهولست و کمک آدولف کوتله در دهه ۱۸۳۰ و ۱۸۴۰ توسعه یافت و «لجستیک» نامگذاری شد.[20]
تابع لجستیک بهطور مستقل در شیمی برای مدلسازی واکنش خودکاتالیزی توسعه یافت.[21] واکنش خودکاتالیزی یک واکنش شیمیایی است که یکی از محصولات واکنش خود یک فروکافت برای همان واکنش یا یک واکنش جفت باشد.[22]
تابع لجستیک بهطور مستقل به عنوان مدلی برای پیشبینی رشد جمعیت در سال ۱۹۲۰ توسط ریموند پرل و لاول رید دوباره ایجاد و به چاپ رسید که منجر به استفاده آن در علم آمار شد. آنها در ابتدا این مدل را برای مدلسازی جمعیت ایالات متحده آمریکا به کار گرفته بودند.[23] ریموند پرل و لاول رید در ابتدا از کار ورهولست بیخبر بودند و احتمالاً در مورد آن از گوستاو دو پاسگیر آگاهی یافتند، اما اعتبار کمی به او دادند و اصطلاحات او را اتخاذ نکردند.[24] تقدم کار ورهولست بعدها مورد تأکید قرار گرفت و اصطلاح «لجستیک» توسط اودنی یول در سال ۱۹۲۵ احیا شد و از آن زمان مورد استفاده قرار گرفت.[25]
در دهه ۱۹۳۰، مدل پروبیت توسط چستر ایتنر بلیس و جان گادوم ابداع شد و اصطلاح «پروبیت» برای آن مورد استفاده قرار گرفت. فیشر کمی بعدتر مدل پروبیت را با تخمین از طریق برآورد درستنمایی بیشینه توسعه داد. مدل پروبیت در ابتدا اساساً برای زیست سنجی مورد استفاده قرار میگرفت و پیش از آن هم در کارهای مشابهی در این زمینه در دهه ۱۸۶۰ از آن استفاده میشد. مدل پروبیت بر توسعه بعدی رگرسیون لجستیک تأثیر گذاشت؛ این دو مدل رقیب یکدیگر بودند.[26]
مدل لجستیک احتمالاً برای اولین بار به عنوان جایگزینی برای مدل پروبیت در زیست سنجی توسط ادوین بیدول ویلسون و شاگردش جین ورسستر در مورد استفاده قرار گرفت.[27] با این حال، توسعه مدل لجستیک به عنوان یک جایگزین کلی برای مدل پروبیت، عمدتاً ناشی از کار جوزف برکسون طی چند دهه بود. وی کلمه «لوجیت» را با قیاس به «پروبیت» ایجاد کرد.[28] مدل لوجیت در ابتدا به عنوان مدلی ضعیفتر از پروبیت رد شد،[29] اما به تدریج به برابری با مدل پروبیت دست یافت و بعد از آن پیشیگرفت. این محبوبیت نسبی بخاطر سادگی محاسباتی، خصوصیات ریاضی و کلی بودن مدل بود که اجازه استفاده از آن را در حوزههای گوناگون میداد.[30] دیوید کاکس بعدها اصلاحات فراوانی بر روی مدل لوجیت اعمال کرد.[31]
با توسعه مدل لوجیت به مدلی چندجملهای دامنه کاربرد و محبوبیت مدل به شدت افزایش پیدا کرد.[32]
جستارهای وابسته
- تحلیل تفکیک خطی
- پرسپترون
- شبکه عصبی مصنوعی
- کاوشهای ماشینی در دادهها
- رگرسیون خطی
- رگرسیون پواسون
منابع
- Hosmer, David W. ; Lemeshow, Stanley (2000). Applied Logistic Regression (2nd ed.). Wiley. ISBN 978-0-471-35632-5.
- Bühlmann, Peter; van de Geer, Sara (2011). "Statistics for High-Dimensional Data". Springer Series in Statistics. doi:10.1007/978-3-642-20192-9. ISSN 0172-7397.
- Bühlmann, Peter; van de Geer, Sara (2011). Theory for ℓ1/ℓ2-penalty procedures. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 249–291. doi:10.1007/978-3-642-20192-9_8. ISBN 9783642201912.
- Bishop, C. M. (2006), Pattern Recognition and Machine Learning, Springer, p. 146, ISBN 978-0-387-31073-2
- Bishop, Christopher (2006). Pattern Recognition and Machine Learning. New York: Christopher. ISBN 9780387310732.
- Natarajan, B. K. (1995). "Sparse Approximate Solutions to Linear Systems". SIAM Journal on Computing. 24 (2): 227–234. doi:10.1137/s0097539792240406. ISSN 0097-5397.
- Bishop, Christopher M (2016-08-23). Pattern Recognition and Machine Learning (به English). New York: Springer New York. p. 30. ISBN 9781493938438.
- Robert, Christian (2014-04-03). "Machine Learning, a Probabilistic Perspective". CHANCE. 27 (2): 62–63. doi:10.1080/09332480.2014.914768. ISSN 0933-2480.
- Boyd, C. R.; Tolson, M. A.; Copes, W. S. (1987). "Evaluating trauma care: The TRISS method. Trauma Score and the Injury Severity Score". The Journal of Trauma. 27 (4): 370–378. doi:10.1097/00005373-198704000-00005. PMID 3106646.
- Kologlu, M.; Elker, D.; Altun, H.; Sayek, I. (2001). "Validation of MPI and PIA II in two different groups of patients with secondary peritonitis". Hepato-Gastroenterology. 48 (37): 147–51. PMID 11268952.
- Biondo, S.; Ramos, E.; Deiros, M.; Ragué, J. M.; De Oca, J.; Moreno, P.; Farran, L.; Jaurrieta, E. (2000). "Prognostic factors for mortality in left colonic peritonitis: A new scoring system". Journal of the American College of Surgeons. 191 (6): 635–42. doi:10.1016/S1072-7515(00)00758-4. PMID 11129812.
- Marshall, J. C.; Cook, D. J.; Christou, N. V.; Bernard, G. R.; Sprung, C. L.; Sibbald, W. J. (1995). "Multiple organ dysfunction score: A reliable descriptor of a complex clinical outcome". Critical Care Medicine. 23 (10): 1638–52. doi:10.1097/00003246-199510000-00007. PMID 7587228.
- Le Gall, J. R.; Lemeshow, S.; Saulnier, F. (1993). "A new Simplified Acute Physiology Score (SAPS II) based on a European/North American multicenter study". JAMA. 270 (24): 2957–63. doi:10.1001/jama.1993.03510240069035. PMID 8254858.
- David A. Freedman (2009). Statistical Models: Theory and Practice. Cambridge University Press. p. 128.
- Truett, J; Cornfield, J; Kannel, W (1967). "A multivariate analysis of the risk of coronary heart disease in Framingham". Journal of Chronic Diseases. 20 (7): 511–24. doi:10.1016/0021-9681(67)90082-3. PMID 6028270.
- Harrell, Frank E. (2001). Regression Modeling Strategies (2nd ed.). Springer-Verlag. ISBN 978-0-387-95232-1.
- M. Strano; B.M. Colosimo (2006). "Logistic regression analysis for experimental determination of forming limit diagrams". International Journal of Machine Tools and Manufacture. 46 (6): 673–682. doi:10.1016/j.ijmachtools.2005.07.005.
- Palei, S. K.; Das, S. K. (2009). "Logistic regression model for prediction of roof fall risks in bord and pillar workings in coal mines: An approach". Safety Science. 47: 88–96. doi:10.1016/j.ssci.2008.01.002.
- Berry, Michael J.A (1997). Data Mining Techniques For Marketing, Sales and Customer Support. Wiley. pp. 10.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 3–5. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 7. doi:10.2139/ssrn.360300.
- Steinfeld J.I. , Francisco J.S. and Hase W.L. Chemical Kinetics and Dynamics (2nd ed. , Prentice-Hall 1999) p.151-2 شابک ۰−۱۳−۷۳۷۱۲۳−۳
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 5. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 6. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 6–7. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 7–9. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 9. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 8. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 11. doi:10.2139/ssrn.360300.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 10–11. doi:10.2139/ssrn.360300.
- Walker, SH; Duncan, DB (1967). "Estimation of the probability of an event as a function of several independent variables". Biometrika. 54 (1/2): 167–178. doi:10.2307/2333860. JSTOR 2333860.
- Cramer, J. S. (2002-12-01). "The Origins of Logistic Regression". Rochester, NY: 13. doi:10.2139/ssrn.360300.