میانه (آمار)

میانه (به انگلیسی: Median) در آمار و نظریه احتمالات یکی از سنجش‌های گرایش به مرکز است. میانه عددی است که یک جمعیت آماری یا یک توزیع احتمالی را به دو قسمت مساوی تقسیم می‌کند. یکی از مزیت‌های مهم میانه نسبت به میانگین این است که میانه از اعداد بسیار بزرگ و بسیار کوچک مجموعهٔ اندازه‌ها متأثر نمی‌شود.[1]

یکی از مهم‌ترین خاصیت میانه این است که مجموع قدر مطلق تفاوت‌های مقادیر مختلف متغیر تصادفی از میانه کمینه است.[2] یعنی:

${\displaystyle \sum _{i=1}^{N}|x_{i}-M|=min}$

بررسی میانه در مجموعه متناهی

دو مثال از میانه در دو مجموعه متناهی فرد عضوی و زوج عضوی

برای پیدا کردن میانه در یک مجموعه ${\displaystyle N}$ عضوی:

1. ابتدا باید اعداد را از کوچک به بزرگ مرتب کرد.
2. اگر تعداد اعداد مجموعه مرتب شده، فرد باشد عدد وسط میانه (عدد ردیف ${\displaystyle {\frac {N+1}{2}}}$) خواهد بود.[3] به‌طور مثال در مجموعه هفت عضوی {۱٬۳٬۳٬۵٬۷٬۸٬۹} میانه عدد چهارم یعنی ۵ است.
3. اگر تعداد اعداد مجموعه مرتب شده، زوج باشد، میانه برابر میانگین دو عدد میانی (عددهای ردیف ${\displaystyle {\frac {N}{2}}}$ و ${\displaystyle {\frac {N}{2}}+1}$) خواهد بود.[4] به‌طور مثال در مجموعه هشت عضوی {۱٬۲٬۳٬۳٬۵٬۶٬۷٬۱۰} میانه برابر میانگین اعداد چهارم و پنجم (۳ و ۵)، یعنی ۴ خواهد بود.

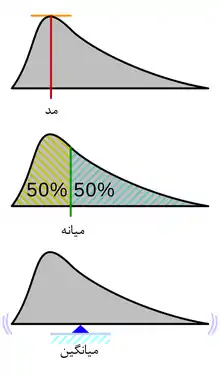
مقایسه میانه، میانگین و مد

مقایسه مشترک شاخص‌های مرکزی در مجموعه { ۱۰, ۷, ۶, ۵, ۳, ۳, ۲, ۱ }

نوع	توضیح	مثال	نتیجه
میانگین حسابی	جمع ارزش یک مجموعه داده تقسیم بر تعداد ارزش‌ها: ${\displaystyle \scriptstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$	۸ / (۱+۲+۳+۳+۵+۶+۷+۱۰)	۴٫۶۲۵
میانه (آمار)	ارزش عددی واقع شده در وسط یک مجموعه داده پس از حذف بزرگترین و کوچکترین داده از مجموعه	۱۰, ۷, ۶, ۵, ۳, ۳, ۲, ۱	۴=۲÷(۳+۵)
مد	پر تکرارترین ارزش در یک مجموعه داده	۱۰, ۷, ۶, ۵, ۳, ۳, ۲, ۱	۳

محاسبه‌ی میانه در داده‌های طبقه بندی شده

ابتدا از فرمول ${\displaystyle {\frac {N}{2}}}$ محل میانه به دست می‌آید. سپس در ستون فراوانی تجمعی، اولین ستونی که فراوانی تجمعی آن بزرگ‌تر یا مساوی ${\displaystyle {\frac {N}{2}}}$ در نظر گرفته می‌شود. میانه از رابطه زیر به دست می‌آید.

${\displaystyle me=L_{i}+{\frac {{\frac {N}{2}}-F_{i-1}}{f_{i}}}C}$

که ستون ${\displaystyle i}$م ستون شامل میانه، ${\displaystyle F_{i}}$ فراوانی تجمعی ستون پیشین ستون شامل میانه، ${\displaystyle L_{i}}$ حد پایین طبقه میانه‌دار، ${\displaystyle f_{i}}$ فراوانی ستون شامل میانه، ${\displaystyle C}$ طول بازه و ${\displaystyle N}$ تعداد داده‌ها است.

به‌طور مثال در جدول توزیع فراوانی زیر:

بازه	۵ تا ۹	۱۰ تا ۱۴	۱۵ تا ۱۹	۲۰ تا ۲۴
فراوانی (${\displaystyle f_{i}}$)	۳	۷	۴	۴
فراوانی تجمعی	۳	۱۰	۱۴	۱۸

${\displaystyle {\frac {N}{2}}={\frac {18}{2}}=9\rightarrow }$میانه در ستون دوم است

${\displaystyle me=L_{2}+({\frac {{\frac {N}{2}}-F_{1}}{f_{1}}})C=9.5+({\frac {9-3}{7}})\times 5=13.79}$

پس میانه در جدول توزیع فراوانی بالا برابر ۱۳٫۷۹ است.

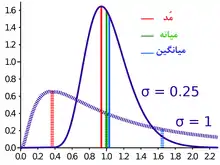
میانه در توزیع متغیر تصادفی پیوسته

نمایش مد، میانه و میانگین در یک تابع توزیع احتمال.[5]

برای هر توزیع احتمال f با تابع توزیع تجمعی F میانه m نقطه‌ای نقطه‌ای تعریف می‌شود که:

${\displaystyle \operatorname {P} (X\leq m)\geq {\frac {1}{2}}{\text{ و }}\operatorname {P} (X\geq m)\geq {\frac {1}{2}}\,\!}$

نامساوی‌های بالا را می‌توان به شکل انتگرالی نیز نشان داد:

${\displaystyle \int _{(-\infty ,m]}dF(x)\geq {\frac {1}{2}}{\text{ و }}\int _{[m,\infty )}dF(x)\geq {\frac {1}{2}}\,\!}$

با توجه به این که تابع توزیع احتمال f برابر با مشتق تابع توزیع تجمعی F است داریم:

${\displaystyle \operatorname {P} (X\leq m)=\operatorname {P} (X\geq m)=\int _{-\infty }^{m}f(x)\,dx=\int _{m}^{\infty }f(x)\,dx={\frac {1}{2}}.\,\!}$

مقایسه مُد، میانه و میانگین در دو توزیع لگاریتمی نرمال با انحراف معیارهای متفاوت

جستارهای وابسته

• میانگین
• مد
• چارک
• دهک
• پراکندگی

منابع

1. هادی رنحبران، آمار و احتمال، ۱۴.
2. هادی رنحبران، آمار و احتمال، ۱۴.
3. هادی رنحبران، آمار و احتمال، ۱۳.
4. هادی رنحبران، آمار و احتمال، ۱۳.
5. "AP Statistics Review - Density Curves and the Normal Distributions". Archived from the original on 2 April 2015. Retrieved 16 March 2015.

برای مطالعهٔ بیشتر

• رنجبران، هادی (۱۳۸۴). آمار و احتمال. تهران: نشر کتب دانشگاهی.
• مشارکت‌کنندگان ویکی‌پدیا. «Median». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۶ مارس ۲۰۰۸.