متغیر تصادفی

در آمار و احتمال، متغیر تصادفی[1] یا ورتنده کاتوره [2] متغیری است که مقدار آن از اندازه‌گیری برخی از انواع فرایندهای تصادفی بدست می‌آید. به‌طور رسمی‌تر، متغیر تصادفی تابعی است از فضای نمونه به اعداد حقیقی. به‌طور مستقیم متغیر تصادفی توصیف عددی خروجی یک آزمایش است (مثل برآمدهای ممکن از پرتاب دو تاس (۱و۱) و (۱و۲) و غیره).

متغیر تصادفی تابعی‌است که فضای نمونه‌ای را به مقادیر اعداد حقیقی مرتبط می‌کند.

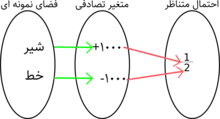
متغیرهای تصادفی به دو نوع گسسته (متغیر تصادفی که ممکن است تعداد محدود یا توالی نامحدودی از مقادیر را بگیرد) و پیوسته (متغیری که ممکن است هر مقدار عددی در یک یا چند بازه را بگیرد) طبقه‌بندی می‌شوند. مقادیر ممکن یک متغیر تصادفی می‌تواند نشان‌دهندهٔ برآمدهای آزمایشی که هنوز انجام نشده یا مقادیر بالقوهٔ یک کمیت که مقدارهای موجود آن نامطمئن هستند (مثلاً در نتیجه اطلاعات ناقص یا اندازه‌گیری نادقیق) باشد. یک متغیر تصادفی می‌تواند به عنوان یک کمیت که مقدارش ثابت نیست و مقادیر مختلفی را می‌تواند بگیرد در نظر گرفته شود و توزیع احتمال برای توصیف احتمال اتفاق افتادن آن مقادیر استفاده می‌شود.

متغیرهای تصادفی معمولاً با اعداد حقیقی مقداردهی می‌شوند؛ ولی می‌توان انواع دلخواهی مانند مقدارهای بولی، اعداد مختلط، بردارها، ماتریس‌ها، دنباله‌ها، درخت‌ها، مجموعه‌ها، شکل‌ها، منیوفیلدها، توابع و فرایندها را در نظر گرفت. عبارت المان تصادفی همه این نوع مفاهیم را دربرمی گیرد.

متغیرهای تصادفی که با اعداد حقیقی مقداردهی می‌شوند، در علوم برای پیش‌بینی براساس داده‌های بدست آمده از آزمایش‌های علمی استفاده می‌شوند. علاوه بر کاربردهای علمی، متغیرهای تصادفی برای آنالیز بازی‌های قمار و پدیده‌های تصادفی به وجود آمدند. در چنین مواردی تابعی که خروجی را به یک عدد حقیقی می‌نگارد معمولاً یک تابع همانی یا به‌طور مشابه یک تابع بدیهی است و به‌طور صریح توصیف نشده‌است. با این وجود در بسیاری از موارد بهتر است متغیر تصادفی را به صورت توابعی از سایر متغیرهای تصادفی در نظر بگیریم که دراینصورت تابع نگاشت استفاده شده در تعریف یک متغیر تصادفی مهم می‌شود. به عنوان مثال، توان دو یک متغیر تصادفی با توزیع استاندارد (نرمال) خود یک متغیر تصادفی با توزیع کی دو است. شهود این مطلب بدین صورت است که تصور کنید اعداد تصادفی بسیاری با توزیع نرمال تولید کرده و هرکدام را به توان دو برسانیم و سپس هیستوگرام داده‌های بدست آمده را بکشیم در اینصورت اگر داده‌ها به تعداد کافی باشند، نمودار هیستوگرام تابع چگالی توزیع کی دو را با یک درجه آزادی تقریب خواهد زد.

نام‌های دیگر

در برخی از کتاب‌های قدیمی‌تر به جای «متغیر تصادفی» اصطلاح‌های «متغیر شانسی» و «متغیر استوکاستیکی» هم به کار رفته‌است.[3]

انواع

• متغیر تصادفی گسسته

انواع متغیر تصادفی گسسته: ۱. برنولی ۲. دو جمله‌ای ۳. دو جمله‌ای منفی ۴. پواسون ۵. هندسی ۶. فوق هندسی ۷. زتا

• متغیر تصادفی پیوسته

انواع متغیر تصادفی پیوسته:۱. تکنواخت ۲. نمایی ۳. نرمال ۴. گاما ۵. بتا ۶. کشی 7. t استیودنت

با توجه به وضع شمارایی فضای نمونه‌ای S، متغیر می‌تواند گسسته یا پیوسته باشد. اگر S متناهی یا نامتناهی شمارا باشد متغیر تصادفی X گسسته و اگر ناشمارا باشد X پیوسته خواهد بود.

یک توزیع همچنین می‌تواند از نوع مختلط (mixed) باشد به این صورت که بخشی از آن مقادیر خاصی را بگیرد و بخش دیگر آن مقادیر روی یک بازه را بگیرد.

/* انواع */ متغیر تصادفی گسسته: { برنولی، دوجمله‌ای، پوآسن، هندسی، دو جمله‌ای منفی، فوق هندسی، زتا (زیپ اف) } متغیر تصادفی پیوسته: { یکنواخت، نرمال، نمایی، گاما، وایبل، کُشـِی، بتا، tاستیودِنت، خِی۲(کای اسکُوِر) , f(فیشر) }

متغیرهای تصادفی گسسته:

متغیر تصادفی برنولی: یک برد وباخت ساده است؛ که مربوط به یک آزمایش برد و باخت ساده است و فقط مقادیر ۰٬۱ را می‌پذیرد. احتمال موفقیت را با p و احتمال شکست را با q نشان می‌دهند. مثال: در یک سکهٔ سالم احتمال ظاهر شدن شیر ۲برار احتمال ظاهر شدن خط است اگر xتعداد شیرهای ظاهر شده در یکبار پرتاب سکه باشد جدول احتمال xرا تشکیل دهید.

متغیر تصادفی دوجمله ای: از تکرار آزمایش برنولی تعداد nبار متغیر تصادفی دو جمله‌ای حاصل می‌شود. مثال:یک سکه سالم ۳بار پرتاب می‌شود (یا ۳سکه پرتاب می‌شود) اگر xتعداد شیرهای ظاهر شده باشد مجموع مقادیر x عبارت است از: {۰٬۱٬۲٬۳}=(p(x

متغیر تصادفی هندسی (متغیر هندسی): اگر یک آزمایش برنولی آنقدر تکرار شود تا اولین موفقیت ظاهر شود تعداد دفعات تکرار آزمایش را متغیر تصادفی است که متغیر تصادفی هندسی نامیده می‌شود. مثال:یک سکه سالم آنقدر پرتاب می‌شود تا اولین شیر ظاهر شود احتمال آزمایش پس از ۱۰دفعه پرتاب تا زمانی که متوقف شود.

متغیر تصادفی دو جمله‌ای منفی: اگر یک آزمایش برنولی آنقدر تکرار شود تا kاُمین موفقیت ظاهر شود آنگاه تعداد دفعات تکرار آزمایش یک متغیر تصادفی است، که متغیر تصادفی دوجمله‌ای منفی نامیده می‌شود. مثال:یک سکهٔ سالم آنقدر پرتاب می‌شود که (سومین) شیر ظاهر شود، احتمال متوقف شدن آزمایش در پرتاب هشتم.

متغیر تصادفی فوق هندسی: اگر در جامعه‌ای به حجم K ,N نفر دارای یک ویژگی بخصوص باشند و از این جامعه یک نمونه به حجم n انتخاب کنیم در صورتی که تعداد اعضای نمونه که دارای آن ویژگی هستند را با x نشان دهیم آنگاه x یک متغیر تصادفی است که متغیر تصادفی فوق هندسی نامیده می‌شود. مثال: ۲۵٪ پنالتی‌های یک بازیکن بسکتبال وارد سبد نمی‌شود احتمال اولین پنالتی داخل سبد پس از ۶پرتاب.

متغیر تصادفی پواسون: تعداد آزمایش‌های تصادفی که در یک محدوده مشخص رخ می‌دهد متغیر تصادفی پواسون نامیده می‌شود. مثال: تعداد پست‌های خالی که (در طول یک سال) در دیوان عالی ایجاد می‌شود.

چند مثال

نتایج ممکن برای آزمایش پرتاب سکه شیر و خط است پس { شیر، خط }=${\displaystyle \Omega }$ می‌توانیم متغیر تصادفی ${\displaystyle Y}$ را به صورت زیر تعریف کنیم

${\displaystyle Y(\omega )={\begin{cases}1,&{\text{if}}\ \ \omega ={\text{heads}},\\0,&{\text{if}}\ \ \omega ={\text{tails}}.\end{cases}}}$

اگر فرض کنیم که احتمال شیر یا خط آمدن یکسان و برابر ${\displaystyle 0.5}$ است آنگاه تابع جرمی احتمال (pmf) به صورت زیر است.

${\displaystyle \rho _{Y}(y)={\begin{cases}{\frac {1}{2}},&{\text{if }}y=1,\\{\frac {1}{2}},&{\text{if }}y=0.\end{cases}}}$

برای توصیف نتیجه یک پرتاب تاس نیز می‌توان از متغیر تصادفی استفاده کرد فضای حالت را به شکل مجموعه {۱، ۲، ۳، ۴، ۵، ۶}=${\displaystyle \Omega }$ زیر در نظر می‌گیریم اگر متغیر تصادفی X را مساوی با نتیجه تاس تعریف کنیم آنگاه:

${\displaystyle X(\omega )={\begin{cases}1,&{\text{if a 1 is rolled}},\\2,&{\text{if a 2 is rolled}},\\3,&{\text{if a 3 is rolled}},\\4,&{\text{if a 4 is rolled}},\\5,&{\text{if a 5 is rolled}},\\6,&{\text{if a 6 is rolled}}.\end{cases}}}$

و pmf این متغیر به صورت زیر خواهد بود.

${\displaystyle \rho _{X}(x)={\begin{cases}{\frac {1}{6}},&{\text{if }}x=1,2,3,4,5,6,\\0,&{\text{otherwise}}.\end{cases}}}$

به عنوان یک مثال برای حالت پیوسته یک دیسک گردان که با چرخش خود می‌تواند جهتی را در افق مشخص کند در نظر بگیرید می‌توانیم جهت را با شمال و شمال شرق و … نشان دهیم اما متداول‌تر است که جهات را به اعداد حقیقی نسبت دهیم. برای این کار فرض می‌کنیم که نتیجه آزمایش را با زاویه‌ای که با سمت شمال می‌سازد توصیف کنیم در این صورت متغیر تصادفی می‌تواند مقادیر بازه (۰٬۳۶۰] را بگیرد. در این حالت اگر X را به عنوان متغیر تصادفی برابر با زاویه با شمال قرار دهیم احتمال وقوع هر X حقیقی برابر ۰ خواهد بود اما احتمال انتخاب شدن یک بازه مقداری بزرگتر از صفر خواهد بود برای مثال احتمال این که X در بازه [۰٬۱۸۰] قرار داشته باشد برابر ۰٫۵ است. در این حالت به جای استفاده از تابع جرمی احتمال از تابع چگالی احتمال استفاده می‌کنیم و می‌گوییم که چگالی احتمال X برابر ۱/۳۶۰ است و احتمال قرار گرفتن X در بازه‌ای به طول L برابر L/۳۶۰ است در حالت کلی برای حساب کردن احتمال قرار گرفتن X در یک بازه باید از تابع چگالی احتمال روی آن بازه انتگرال بگیریم.

یک مثال برای حالت مختلط این است که سکه را برتاب کنیم و در صورت این مه نتیجه شیر بود دیسک را بجرخانیم اگر نتیجه خط بود X=-۱ و اگر شید بود X برابر با زاویه با شمال است در این صورت احتمال X=-۱ برابر ۰٫۵ خواهد بود و احتمال حالت پیوسته را نیز با توجه به مثال قبل می‌توان حساب کرد (چگالی احتمال برابر ۱/۷۲۰ است).

تابع توزیع تجمعی

تابع توزیع تجمعی متغیر تصادفی X به شکل زیر تعریف می‌شود.

${\displaystyle F_{X}(x)=\operatorname {P} (X\leq x)}$

به عبارتی این تابع احتمال این که نتیجه از عددی خاص کوچکتر باشد را به ما می‌دهد. برخی از خواص این تابع در زیر آمده‌است.

۱-تابع ${\displaystyle F_{X}(x)}$ تابعی صعودی است.

۲- ${\displaystyle F_{X}(\infty )=1}$ ${\displaystyle lim_{x\to \infty }F_{X}(x)=}$ (حد در بی‌نهایت)

۳- ${\displaystyle F_{X}(-\infty )=0}$ ${\displaystyle lim_{x\to -\infty }F_{X}(x)=}$

تابع یک متغیر تصادفی

اگر X یک متغیر تصادفی روی ${\displaystyle \Omega \,\!}$ باشد و ${\displaystyle g:\mathbb {R} \rightarrow \mathbb {R} }$ باشد آنگاه ${\displaystyle Y=g(X)\,\!}$ نیز یک متغیر تصادفی روی ${\displaystyle \Omega \,\!}$ خواهد بود. تابع توزیع تجمعی ${\displaystyle Y}$ از رابطه زیر تبعیت می‌کند

${\displaystyle F_{Y}(y)=\operatorname {P} (g(X)\leq y).}$

اگر g معکوس پذیر باشد یعنی g^−۱ وچود داشته باشد و با فرض صعودی بودن g می‌توان به رابطه زیر رسید.

${\displaystyle F_{Y}(y)=\operatorname {P} (g(X)\leq y)=\operatorname {P} (X\leq g^{-1}(y))=F_{X}(g^{-1}(y))}$

با فرض معکوس‌پذیری و مشتق‌پذیری می‌توان با مشتق گرفتن از دو طرف رابطه بالا نسبت به y رابطه‌ای بین دو تابع چگالی احتمال نیز پیدا کرد که به شکل زیر است.

${\displaystyle f_{Y}(y)=f_{X}(g^{-1}(y))\left|{\frac {dg^{-1}(y)}{dy}}\right|}$.

اکر رابطه معگوس‌پذیری برقرار نباشد اما تعداد ریشه‌های g برای هر مقدار y تعداد شمارایی باشد (یعنی تعداد محدود یا شمارا نامحدودی ریشه برای (y = g(x_i داشته باشیم) رابطه بین دو تابع چگالی احتمال به صورت زیر در می‌آید.

${\displaystyle f_{Y}(y)=\sum _{i}f_{X}(g_{i}^{-1}(y))\left|{\frac {dg_{i}^{-1}(y)}{dy}}\right|}$

که (x_i = g_i^-۱(y.

مثال۱

فرض کنید که X یک متغیر تصادفی پیوسته و حقیقی مقدار باشد و Y = X^۲.

${\displaystyle F_{Y}(y)=\operatorname {P} (X^{2}\leq y).}$

اگر y <۰ آنگاه P(X ^۲ ≤ y) = ۰، پس

${\displaystyle F_{Y}(y)=0\qquad {\hbox{if}}\quad y<0.}$

اگر y ≥ ۰ آنگاه:

${\displaystyle \operatorname {P} (X^{2}\leq y)=\operatorname {P} (|X|\leq {\sqrt {y}})=\operatorname {P} (-{\sqrt {y}}\leq X\leq {\sqrt {y}}),}$

پس

${\displaystyle F_{Y}(y)=F_{X}({\sqrt {y}})-F_{X}(-{\sqrt {y}})\qquad {\hbox{if}}\quad y\geq 0.}$

مثال ۲

فرض کنید X یک متغیر تصادفی با CDF زیر باشد که ${\displaystyle \theta }$ یک مقدار ثابت و بزرگتر از صفر است.

${\displaystyle F_{X}(x)=P(X\leq x)={\frac {1}{(1+e^{-x})^{\theta }}}}$

و تابع y با ضابطه ${\displaystyle \scriptstyle Y=\mathrm {log} (1+e^{-X}).}$ داده شده‌است.

داریم:

${\displaystyle F_{Y}(y)=P(Y\leq y)=P(\mathrm {log} (1+e^{-X})\leq y)=P(X>-\mathrm {log} (e^{y}-1)).\,}$

عبارت بالا برحسب تابع توزیع تجمعی X قابل محاسبه است بنابراین

${\displaystyle F_{Y}(y)=1-F_{X}(-\mathrm {log} (e^{y}-1))\,}$

${\displaystyle =1-{\frac {1}{(1+e^{\mathrm {log} (e^{y}-1)})^{\theta }}}}$

${\displaystyle =1-{\frac {1}{(1+e^{y}-1)^{\theta }}}}$

${\displaystyle =1-e^{-y\theta }.\,}$

(منظور از log لگاریتم طبیعی (Ln) است)

تساوی دو متغیر تصادفی

تعابیر مختلفی برای تساوی دو متغیر تصادفی وجود دارد. دو متغیر می‌توانند مساوی باشند یا در توزیع مساوی باشند (equal in distribution) یا تقریباً همه جا برابر (almost surely equality) باشند.

تساوی در توزیع

اگر دو تابع X و Y تابع توزیع یکسانی داشته باشند می‌گوییم در توزیع مساوی هستند

${\displaystyle \operatorname {P} (X\leq x)=\operatorname {P} (Y\leq x)\quad {\hbox{for all}}\quad x.}$

دو توزیع که تابع مولد گشتاور یکسانی دارند در توزیع مساوی هستند.

تقریباً همه جا برابر یا قریب به یقین برابر

این تساوی در صورتی برقرار است که احتمال تفاوت X و Y صفر باشد.

${\displaystyle \operatorname {P} (X\neq Y)=0.}$

تساوی

دو متغیر تصادفی X و Y مساوی هستند اگر به عنوان تابع روی فضای نمونه یکسان باشند

${\displaystyle X(\omega )=Y(\omega )\qquad {\hbox{for all }}\omega .}$

جستارهای وابسته

• توزیع احتمال

پانویس

1. «متغیر تصادفی» [آمار، ریاضی] هم‌ارزِ «random variable»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر ششم. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۸۵-۶ (ذیل سرواژهٔ متغیر تصادفی)
2. https://paarsig.com/random
3. فرند. پانویس ص. ۸۴

منابع

• فروند، جان. آمار ریاضی؛ ترجمه علی حمیدی، محمدقاسم وحیدی‌اصل. تهران: مرکز نشر دانشگاهی، ۱۳۷۸. شابک ‎۹۶۴-۰۱-۰۹۱۶-۹

http://en.wikipedia.org/w/index.php?title=Random_variable&oldid=437209168

Sheldon Ross ,Introduction to Probability Models Tenth Edition page 25